Многочлены. Сложение и умножение многочленов.
Пусть Р- некоторое числовое поле, х — переменная, x0, х1, х2…хn-степени переменной.
Определение 1. Формальное выражение вида an*хn+аn-1*хn-1+…+а0 (1),
где аn,…а0ÎР называют многочленом над полем Р от переменной х, аn,…а0 — коэффициенты многочлена.
Если аn¹0,то an*хn называется старшим членом многочлена, аn — старший коэффициент многочлена. n=deg (многочлена) — степень многочлена.
Множество многочленов над полем Р будем обозначать через Р[х], при этом многочлены будем обозначать так: f(x),g(x)…
В анализе обычно смотрят на многочлен как на функцию. Степень многочлена, у которого все коэффициенты равны нулю будем считать неопределенной. Иногда нулевому многочлену приписывают степень, равную -¥. Это бывает удобно и не приводит к противоречию. Часто бывает удобным записывать многочлен не по убывающим степеням x, а по возрастающим и применять другую нумерацию коэффициентов.
Определение 2. Два многочлена называют равными, если равны их коэффициенты, стоящие при одинаковых степенях.
Замечание: для многочленов над числовым полем данное определение равенства многочленов совпадает с определением равенства многочленов, если на многочлен смотреть как на функцию.
Сложение многочленов:
f(x)=a0+a1x+…+anxn
g(x)=b0+b1x+…+bsxs , s£n
Под суммой многочленов f(x)+g(x) понимают многочлен
f(x)+g(x)=c0+…+cnxn , где ci=ai+bi.
Очевидно, что сложение многочленов коммутативно и ассоциативно, так как всё сводится к сложению элементов числового поля.
Определение 3. Под произведением многочленов f(x)*g(x) понимают многочлен f(x)*g(x)= d0+…+dn+sxn+s, где 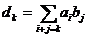 .
.
Упражнение. Доказать, что произведение многочленов коммутативно и ассоциативно, а также дистрибутивно относительно сложения.
§2.Деление многочленов.
Лемма: Пусть f(x), g(x) ÎР[x] — многочлены; f(x) ¹0, g(x) ¹0.
Тогда deg f(x)* g(x)= deg f(x)+deg g(x).
◄Пусть f(x)=a0+a1x+…+anxn , аn¹0,
g(x)=b0+b1x+…+bsxs , bs¹0
f(x)* g(x)=an*bsxn+s+…
Последнее и означает, что степень многочлена равна n+s.
deg f(x)* g(x)=n+s.►
Определение1.Пусть f(x), g(x)ÎР[х]. Будем говорить, что f(x) делит g(x) (обозначать f(x)ïg(x) ), если существует j(х)ÎР[х] такое,что g(x)=f(x)*j(х).
Простейшие свойства:
1)Если g(x) делит fi(x), i=1..n, то g(x) делит 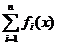 .
.
2)Если f(x) / g(x)и g(x) / m(x), тогда f(x) / m(x).
3)Если f(x) / g(x)и g(x) / f(x), то f(x)=ag(x),где aÎР.
Докажем первое свойство:
◄ g(x) / fi(x) следовательно $ многочлен ji(х), что fi(x) = g(x)ji(х), следовательно
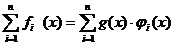
Вынесем общий множитель g(x) за знак суммы. А это и означает, что g(x) делит сумму 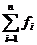 . ►
. ►
Второе свойство доказывается аналогично как и для чисел.
Докажем третье свойство:
◄ f(x) / g(x)®g(x)=f(x)*m(x) (1)
g(x) / f(x)®f(x)=g(x)*q(x) (2)
Подставим (2) в (1):
g(x)=g(x)*q(x)*m(x)  g(x)*(q(x)*m(x)-1)=0
g(x)*(q(x)*m(x)-1)=0  q(x)*m(x)=1.
q(x)*m(x)=1.
Из леммы следует, что степень q(x)= степени m(x)=0.
Иначе говоря, что q(x) и m(x) — это элементы поля P. А это и доказывает свойство 3.►
Теорема о делении с остатком: Пусть f(x), g(x)ÎР[х], g(x)¹0. Тогда существует единственная пара многочленов q(x), r(x)ÎР[х], такая, что f(x)=g(x)*q(x)+r(x), где степень r(x)<степени g(x)либо r(x)=0.
Доказательство. 1) случай: f=0,очевидно q=0, r=0; 2) случай: если степень f<степени g, то q=0 и r=f; 3)случай: ст. f³ст.g.
Пусть
f=an*xn+…+a0,
g=bs*xs+…+b0.
Возьмем многочлен j1=(an/bs)*xn-s . Рассмотрим f-g*j1=f1. Если f1=0, то в качестве r возьмём 0, в качестве q-j1, т.е. r=0; q=j1. Если ст. f1 < ст.g , то в качестве r возьмем f1 , а в качестве q -  1. Если ст. f1
1. Если ст. f1  ст.g, то берем
ст.g, то берем
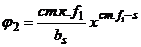 ,
,
f – g  1 = f1 ( ст.f1 < ст.f ),
1 = f1 ( ст.f1 < ст.f ),
f – g  2 = f2 ( ст.f2 < ст.f1 ). C f2 рассуждаем аналогично как и с f1. На
2 = f2 ( ст.f2 < ст.f1 ). C f2 рассуждаем аналогично как и с f1. На
каком-то шаге мы получим, что многочлен fk=0 либо его степень меньше степени g ( степени многочленов fk все время уменьшаются ), где fk-1 - g  k = fk
k = fk
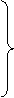 |
f – g  1 = f1 ( ст.f1 < ст.f ) Сложим почленно
1 = f1 ( ст.f1 < ст.f ) Сложим почленно
f1 – g  2 = f2 ( ст.f2 < ст.f1 ) (1) левые и правые части
2 = f2 ( ст.f2 < ст.f1 ) (1) левые и правые части
………………………….. равенств:
fk-1 – g  k = fk
k = fk
__________________________
Получим, что
f – g (  1 +…+
1 +…+  k ) = fk и очевидно
k ) = fk и очевидно
q =  1+…+
1+…+  k ; r = fk.
k ; r = fk.
Этим мы доказали существование q и r.
f = g(  1+…+
1+…+  k ) + fk.
k ) + fk.
Докажем однозначность q и r. Доказывать будем методом от противного. Пусть наряду с разложением f = gq+r (2) имеет место разложение f = gq1+r1 (3). Вычтем из (2) равенство (3). Получим:
r – r1 = g ( q1 – q ).
Сравним степени многочленов слева и справа. Если r-r1≠0, то степень r – r1 < степени -g (q1 – q ). А такого быть не может для равных многочленов. Мы пришли к противоречию. Однозначность доказана.►
Алгоритм Евклида: Пусть f(x) и g(x) — два многочлена над полем Р.
f(x) , g(x)  P[x] ; g(x)
P[x] ; g(x) 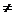 0. Тогда можно разделить с остатком f(x) на g(x).
0. Тогда можно разделить с остатком f(x) на g(x).
f(x)=g(x)q(x)+r(x) , если r(x) 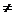 0, степень r(x)<степени g(x).
0, степень r(x)<степени g(x).
Разделим g(x) на r(x) с остатком g(x)=r(x)q1(x)+r1(x), если r1(x) 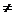 0 степень r1 < степени r.
0 степень r1 < степени r.
Разделим r(x) на r1(x) и т.д.
Так как степени остатков все время убывают, то на каком-то шаге остаток rk+1(x)=0.
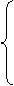 f(x)=g(x)q(x)+r(x) ; r(x)
f(x)=g(x)q(x)+r(x) ; r(x) 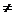 0
0
g(x)=r(x)q1(x)+r1(x) ; r1(x) 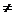 0 ; cт. r1 < ст. r
0 ; cт. r1 < ст. r
(4) r(x)=r1(x)q2(x)+r2(x)
…………………..
rk-1(x)=rk(x)qk+1(x)+rk+1(x), rk+1(x)=0.
Процесс последовательного получения равенств (4) называют алгоритмом Евклида для многочленов f(x) и g(x). Последний отличный от нуля остаток — rk.
§ 3. Наибольший общий делитель многочленов (НОД) 
Определение 1. Пусть f1(x), … , fk(x)  P[x] и
P[x] и 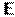 fi(x)
fi(x) 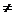 0 (ненулевой набор многочленов). Если
0 (ненулевой набор многочленов). Если 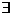 многочлен d(x)
многочлен d(x)  P[x] такой, что:
P[x] такой, что:
1) старший коэффициент d(x) равен 1.
2) d(x) / fi(x)  i=1,…,k
i=1,…,k
3) если h(x)  P[x] обладает свойством h(x) / fi(x)
P[x] обладает свойством h(x) / fi(x)  i , то h(x) / d(x), тогда d(x) называют НОД многочленов f1 ,…, fk
i , то h(x) / d(x), тогда d(x) называют НОД многочленов f1 ,…, fk
Обозначим НОД многочленов f1 ,…, fk через ( f1 ,…, fk).
Выясним вопрос существования, однозначности и нахождения Н.О.Д.
Лемма 1: Пусть f1(x), … , fk(x)  P[x],
P[x],
М={ f1  1+…+ fk
1+…+ fk  k |
k |  1,…,
1,…,  k
k  P[x] } — подмножество P[x]. f, g
P[x] } — подмножество P[x]. f, g  M ; u, v
M ; u, v  P[x] => fu+gv
P[x] => fu+gv  M.
M.
◄ f=f1  1+…+ fk
1+…+ fk  k
k
g = f1 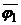 +… +fk
+… +fk 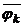
fu+gv= f1(  1u+
1u+ 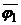 v)+…+ fk(
v)+…+ fk(  ku+
ku+ 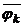 v) очевидно из М.►
v) очевидно из М.►
Теорема 1. ( О существовании НОД)
Пусть f1(x), … , fk(x)  P[x] — некоторые многочлены, среди них есть ненулевой. Тогда многочлен наименьшей степени из М, взятый со старшим коэффициентом 1, является наибольшим общим делителем этих многочленов.
P[x] — некоторые многочлены, среди них есть ненулевой. Тогда многочлен наименьшей степени из М, взятый со старшим коэффициентом 1, является наибольшим общим делителем этих многочленов.
◄Сразу же заметим, что в М есть ненулевой многочлен — fi(x). Докажем, что все fi(x) r=1,…,k в множестве М. По определению М
f1  1+…+ fk
1+…+ fk  k
k 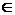 М, если
М, если
 1=1 ;
1=1 ;  2=…=
2=…=  k=0 ; => f1
k=0 ; => f1  M и т.д.
M и т.д.
Очевидно также, что в М есть многочлены со старшим коэффициентом 1 (см. Лемму1):
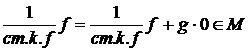 , если
, если 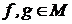 .
.
Среди многочленов со старшим коэффициентом 1 выберем многочлен наименьшей степени. Обозначим его через d(x) и докажем, что это НОД. Во-первых, он со старшим коэффициентом 1 (мы его так выбрали). Во-вторых, d(x) / fi(x)  i. (1)
i. (1)
Докажем (1). Допустим, что 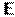 i d(x) ∤ fi(x) , т.е d(x) не делит fi(x). Разделим с остатком fi (x) на d (x): fi(x)=d(x)q(x)+r(x). Выразим r(x):
i d(x) ∤ fi(x) , т.е d(x) не делит fi(x). Разделим с остатком fi (x) на d (x): fi(x)=d(x)q(x)+r(x). Выразим r(x):
M 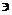 r(x)= fi(x)+d(x)(-q(x)). Согласно Лемме о делении с остатком ст.r < ст.d(x).
r(x)= fi(x)+d(x)(-q(x)). Согласно Лемме о делении с остатком ст.r < ст.d(x).
Если старший коэффициент r(x) равен 1, то сразу же имеем противоречие с выбором d, если же старший коэффициент не равен 1, сделаем, чтобы он стал равен 1:
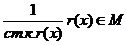 (согласно Лемме 1)
(согласно Лемме 1)
Опять пришли к противоречию.
Докажем условие 3) в определении НОД.
Пусть h(x) | fi(x)  i d(x)= f1
i d(x)= f1  1+…+ fk
1+…+ fk  k
k  M
M  h(x) | d(x) (h(x) делит каждое из слагаемых, значит он делит сумму).►
h(x) | d(x) (h(x) делит каждое из слагаемых, значит он делит сумму).►
!Следствие (основное свойство НОД):
Наибольший общий делитель ненулевого набора многочленов 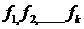 представляется в виде:
представляется в виде:  ,где
,где 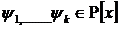 .
.
Это следует из способа доказательства теоремы о существовании НОД, ибо НОД –элемент из М.
Упражнение:Пусть 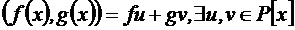 такие, что deg u<deg g, deg v<deg f.
такие, что deg u<deg g, deg v<deg f.
Теорема 2.НОД определен однозначно.
◄Пусть d1 и d2 — наибольшие общие делители многочленов 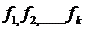 .
.
Тогда d1 делит 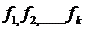 ,то есть d1 │
,то есть d1 │ 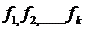 , отсюда следует, что d1 / d2 ( по 3 свойству НОД). Аналогично d1 │ d2 ,значит можно записать d1=аd2 . А так как d1 и d2 со старшим коэффициентом 1,то в качестве а можно взять только единицу (а=1). Значит d1=d2 ,т.е. НОД определен однозначно.►
, отсюда следует, что d1 / d2 ( по 3 свойству НОД). Аналогично d1 │ d2 ,значит можно записать d1=аd2 . А так как d1 и d2 со старшим коэффициентом 1,то в качестве а можно взять только единицу (а=1). Значит d1=d2 ,т.е. НОД определен однозначно.►
Лемма 2.Пусть f(x)=g(x)q(x)+r(x).Тогда наибольший общий делитель f и g равен наибольшему общему делителю g и r, т.е.: ( f, g )=( g, r ).
◄Доказательство теоремы следует из определения. Пусть ( f, g ) = d1 , ( g, r) = d2 .Тогда:
d1 │ f d2 │ g
Þ d1│ r Þ d1 │ d2 и d2 │ d1 Ü d2 │ f Ü
d1 │ g d2│ r
А значит: d1= d2.►
Теорема 3 (об отыскании НОД для двух многочленов).
Пусть f(x), g(x)ÎP[x], g(x)¹0. Тогда НОД многочленов f и g равен последнему, отличному от нуля, остатку в алгоритме Евклида для этих многочленов, взятому со старшим коэффициентом — единица. Если g | f, то НОД ( f, g ) равен 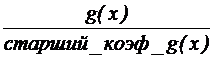 .
.
◄Если g / f ,то последнее утверждение в формулировке теоремы очевидно.
Применяя Лемму 2 к системе равенство (4) предыдущего параграфа, получим ,что
( f, g )=(g,r)=…=( rk ; rk-1 )= 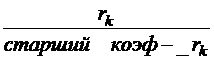 ;
;
P.S. f=gq+r
g=rq1+r1
…………. система (4)
rk-2=rk-1+rk
rk-1 =rkqk+1+0.►
Замечание:
В теореме 3 содержится алгоритм практического отыскания НОД:
ü Ищем последний отличный от нуля остаток в алгоритме Евклида.
ü Делаем его со старшим коэффициентом единица ,это и будет НОД.
Теорема 4.(f1,……….,fk)=((f1,……..,fk-1) , fk ), k≥2.
Эта теорема указывает путь, как процесс нахождения НОД для нескольких многочленов можно свести к нахождению НОД двух многочленов.
◄Доказательство следует из определения НОД.
Критерий взаимной простоты многочленов.►
Определение.Многочлены f1,……….,fk называются взаимно простыми, если их НОД равен единице.
Теорема 5(критерий взаимной простоты).
Многочлены (f1,………., fk ) взаимно простоты тогда и только тогда, когда 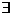 u1,……,uk ÎP[x], такие что единица представляется в виде f1u1 +……+fkuk.
u1,……,uk ÎP[x], такие что единица представляется в виде f1u1 +……+fkuk.
◄Þ Имеем f1,……….,fk взаимно простые, то 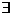 u1,……,uk ÎP[x], такие что f1u1 +……+fkuk=1. Это следует из основного свойства НОД.
u1,……,uk ÎP[x], такие что f1u1 +……+fkuk=1. Это следует из основного свойства НОД.
Ü Пусть d(x)=( f1,……….,fk ). Значит d(x) | 1 Þ d(x)=1 и значит многочлены взаимно простые.►
§ 4. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ МНОГОЧЛЕНОВ (НОК).
Определение. Пусть f1(x),……,fk (x) Î P[x], fi¹0,  fi .Многочлен h(x) называют наименьшим общим кратным многочленов f1(x),……,fk (x), если :
fi .Многочлен h(x) называют наименьшим общим кратным многочленов f1(x),……,fk (x), если :
1) fi (x) | h(x) , т.е. h(x)-общее кратное многочленов;
2)  g(x), являющегося общим кратным, т.е. fi | g ,
g(x), являющегося общим кратным, т.е. fi | g ,  i,
i, 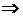 h(x) | g(x). Обозначают НОК таким образом : [f1(x),……,fk (x)] = НОК (f1,……….,fk).
h(x) | g(x). Обозначают НОК таким образом : [f1(x),……,fk (x)] = НОК (f1,……….,fk).
Свойства НОК:
1)[f1,f2] = 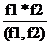 — это дает правило вычисления НОК для двух многочленов;
— это дает правило вычисления НОК для двух многочленов;
2) [f1(x),……,fk (x)] = [f1(x),…fk-1] ,fk (x)] — это свойство сводит вычисление НОК для k многочленов к вычислению НОК для двух многочленов;
3) 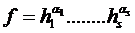 ,
,
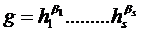 ,
,
[f , g]= 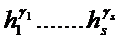 , где
, где 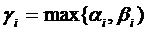 , i=1,…..,s.
, i=1,…..,s.
Всех этих свойств достаточно, чтобы находить НОК для нескольких многочленов.
Упражнение. Однозначен ли НОК (с точностью до постоянного множителя) ?
Докажем свойство 1):
◄Обозначим [f1,f2] через m1 , 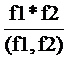 через m2 ,
через m2 , 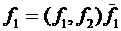 ,
, 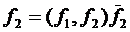 .
.
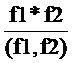 =
= 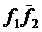 =
= 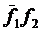 Þ
Þ 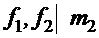 Þ
Þ 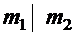 .
.
Если докажем, что 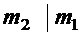 ,т.е. m1 и m2 могут отличаться на постоянный множитель, то m2 будет годиться в качестве НОК.►
,т.е. m1 и m2 могут отличаться на постоянный множитель, то m2 будет годиться в качестве НОК.►
Упражнение. Доказать, что 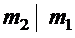 .
.
Докажем свойство 3):
◄ 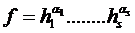
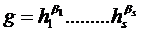
[f,g]= 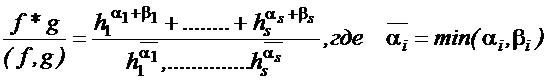 ,
,
то 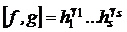 , где
, где 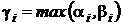 .►
.►
РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА
НЕПРИВОДИМЫЕ МНОЖИТЕЛИ.
Пусть f(x) ÎP[x], степень f(x) ≥ 1, очевидно, что a │ f(x), aÎP, a ≠ 0.
Определение. Многочлен f(x) называется приводимым над полем Р, если в P[x] существуют делители f(x), степени которых больше нуля, и ≠ cm.f, т.е.: f(x)=f1(x)f2(x), причём deg f2 <deg f, deg f1<deg f .
Многочлен f(x) называется неприводимым над полем Р в противном случае, т.е. один из многочленов f1(x) или f2(x) нулевой степени, если f(x)=f1(x)f2(x).
Замечание. Неприводимость многочлена f(x) ÎP[x] зависит от поля, над которым он рассматривается, и есть в этом смысле понятие относительное.
Пример: Многочлен x2 +1 над полем R неприводим, но над полем C он приводим.
Действительно: x2+1=(x-i)(x+i), т.е. приводим надC.
Упражнение. Доказать, что x2-2 неприводим над полем Q, а x2+1 неприводим над полемR.
Простейшие свойства неприводимых многочленов:
1) Всякий многочлен первой степени неприводим (это следует из определения)
f(x)=f1(x)f2(x), deg f(x)=1 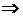 deg f1(x)=0 или 1, deg f2(x)=1 или 0;
deg f1(x)=0 или 1, deg f2(x)=1 или 0;
2) Если f(x) неприводим над полем Р,то аf(x), где aÎP, a ≠ 0, тоже неприводим над полем Р;
3) Если f(x) неприводим над полем Ри g(x) ÎP[x] — некоторый многочлен над P , то ( f(x), g(x) )=1 либо f(x) │ g(x).
◄ Рассмотрим НОД многочленов (f(x), g(x))=d(x).Значит d(x) │ g(x) и d(x) │ f(x) Þ d(x) равен 1, т.е. (f(x), g(x))=1
или 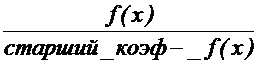 , т.е. f(x) / g(x).►
, т.е. f(x) / g(x).►
4) Если произведение многочленов f(x)g(x) делится на неприводимый многочлен h(x) , то хотя бы один из множителей f(x) или g(x) делится на h(x) ◄ Пусть h(x) ∤ f(x)  => по свойству 3 (h(x),f(x))=1
=> по свойству 3 (h(x),f(x))=1 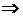
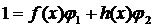 и
и 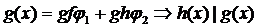 , ибо h(x) │ f(x)g(x) и h(x) │ g(x)h(x).►!
, ибо h(x) │ f(x)g(x) и h(x) │ g(x)h(x).►!
Теорема 1 (о разложении многочлена на неприводимые множители). Всякий многочлен f(x)ÎP[x] степени ≥1 можно представить в виде
произведения неприводимых над P многочленов. Разложение многочлена на неприводимые множители определено однозначно с точностью до многочлена нулевой степени и порядка следования сомножителей, то есть
если имеется два разложения f(x) на неприводимые множители:
f(x)= φ1(x)… φ S(x) = ψ1(x)… ψ k(x) , то s=k и при подходящей нумерации множителей : ψi =aiφi i = 1,…,s 0 ≠aiÎP.
◄Сначала докажем существование:
Если f(x) — неприводим, то в разложении будет один множитель (всё ясно).
Если f(x) приводим, то он представляется в виде f(x) = f1(x)f 2(x). Если f1(x) и f 2(x) — неприводимые, то существование есть.
Если f1(x) или f 2(x) приводим, то с ним поступаем аналогично, как с f(x) и получаем дальше разложение f(x). Этот процесс на каком-то месте оборвётся, так как степени многочленов, которые мы получаем, всё время убывают. Это и доказывает первую часть теоремы.
Докажем вторую часть теоремы — однозначность.
Доказательство будем проводить индукцией по степени f(x). Если степень f(x) равна 1, то всё сводится к свойству 1.Утверждение считаем верным, если степень f(x) < n.Если f(x) неприводим, то доказывать нечего.
Если f(x) приводим, то возьмём разложение:
f(x)= φ1(x)… φ S(x) = ψ1(x)… ψ k(x).
Очевидно, что φ1 делит произведение
φ1 | ψ1(x)… ψ k(x).
Следовательно, по свойству 4 φ1 | ψi => по свойству 2 ψi = aφ1.
После, может быть, перенумерации ψi можно считать ψ1 и Ψ1 =a1φ1.
φ1(x)… φ S(x) = ψ1(x)… ψ k(x)
Сократим обе части равенства на 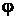 1. Получим
1. Получим
φ 2(x)… φ S(x) = ψ2(x)… ψ k(x) (1)
Обе части равенства (1) представляет собой многочлен степени меньше n. А для многочленов степени меньше n мы имеем индуктивное предположение, из которого следует, что s-1 = k-1 и Ψi =aiφi i=2, …,k после, может быть, перенумерации.►
Замечание1. Мы добьемся полной однозначности в каноническом смысле, если в разложении многочлена на неприводимые множители из каждого сомножителя вынесем его старший коэффициент:
f(x) = a p1(x)… p k(x) ; а – ст. к. f(x). ст. к. pi = 1 (2)
Определение. Если неприводимый многочлен p(x) встречается в разложении (2) несколько раз, то он называется кратным множителем.
Например: если он встречается s раз, то он s-кратным. После этого разложение (2) допускает запись вида (3):
f(x) = a p 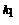 1(x)… p
1(x)… p 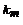 m(x) ; pi ≠ pj (3)
m(x) ; pi ≠ pj (3)
Разложение (3) называют каноническим разложением многочлена на неприводимые. Оно определено однозначно (с точностью до порядка сомножителей).
Замечание 2. Задача о разложении многочлена на неприводимые над произвольным полем до сих пор не решена. Во многих случаях она решена. Мы приведем решение в случаях P=R;С.
Пусть f(x) =рк(x)f1(x), где неприводимый многочлен р(x) не делит f1(x).
Тогда р(x) называют неприводимым множителем кратности к для многочлена f(x)
Теорема 2.Пусть р(x) — к-кратный неприводимый множитель для многочлена f(x). Тогда он является k-1-кратным неприводимым множителем для его производной.
Доказательство. Возьмем производную f(x):
f’(x)=kpk-1(x) p'(x)f1(x)+p(x)kf1'(x) = pk-1(x)(k p'(x) f1(x)+ p(x) f1(x)).
Очевидно, что многочлен в скобках не делится на p(x), что и доказывает теорему.
Упражнение 1. Верно ли обратное утверждение? (вообще говоря, да)
Корни многочлена.
Пусть f(x) — некоторый многочлен над фиксированным полем P. f(x)=anxn+…+a0ÎP[x]. И пусть c — некоторое число (не обязательно из P). Если мы подставим вместо x число c, то получим f(c) = ancn+…+a0 — значение многочлена при x = c. Если f(x)=g(x), то f(c)=g(c).
Определение 1.Если f(c)=0, то с называют корнем многочлена f(x) или корнем уравнения f(х)=0.
Разделим с остатком f(x) на (x-c): f(x)=(x-c)q(x)+r(x), где r(x)=0 и r(x)=aÎR, a¹0, то есть r(x) в любом случае число.
Следующая теорема позволяет найти остаток от деления f(x) на многочлен (x-a) не выполняя самого деления.
Теорема (Безу). Остаток от деления многочлена f(x) на многочлен (x-a) равен значению этого многочлена при x=a.
Упражнение. Привести доказательство.
Следствие. а является корнем f(x) тогда и только тогда,когда (x-а) делит f(x).
◄Þ f(a)=0 (т.к. а-корень). Значит по теореме Безу (x-a) делит
f(x) Ü f(x)=(x-a)f1(x). Очевидно f(a)=0.►
Это позволяет свести нахождение всех корней многочлена к нахождению делителя первой степени. Это можно сделать при помощи схемы Горнера.
Схема Горнера:
Пусть f(x)= a0x n +…+an. Разделим многочлен f(x) на x-a:
f(x)=(x-a ) f 1(x)+r (1)
где
f1 (x)=b0 xn-1+…+bn-1.
Сравним коэффициенты при одинаковых степенях в равенстве (1):
xn : a0=b0
xn-1 : a1=b1-a b0
xn-2 : a2=b2-a b1
…
x  : an = r -a bn-1.
: an = r -a bn-1.
Отсюда имеем:
b0=a0
b1=a1 + a b0
b2=a2+ a b1 (2)
… …
r= an +a bn-1.
Для запоминания вычисления коэффициентов применяют схему Горнера. Делают таблицу следующего вида:
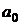 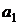 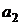 … … 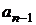 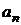 | |
 |  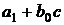 ……………. ……………. |
В первой строке этой таблицы выписывают один за другим все коэффициенты f(x), а во второе слева — элемент 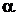 . Коэффициенты частного f1(x) и остаток записывают последовательно во второй строке, согласно равенствам (2).
. Коэффициенты частного f1(x) и остаток записывают последовательно во второй строке, согласно равенствам (2).
§7. Основная теорема алгебры комплексных чисел (Гаусса).
Теорема.Всякий многочлен с любыми числовыми коэффициентами, степень которого больше либо равна единице, имеет хотя бы один корень в поле комплексных чисел.
Эту теорему мы доказывать не будем.
Следствие 1.Многочлен f(x) с любыми числовыми коэффициентами разлагается на линейные множители вида x-α над полем комплексных чисел, причем такое разложение однозначно с точностью до порядка следования сомножителей.
◄ Применяя теорему, получим:
f(x) = (x-α1) f1(x) = (x-α1) (x-α2) f2(x)=…=a 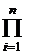 (x-αi), a — коэффициент при старшей степени; П — произведение.►
(x-αi), a — коэффициент при старшей степени; П — произведение.►
Замечание 1. Это следствие решает задачу о разложении многочлена) на неприводимые множители над полем комплексных чисел.
Cледствие 2:Пусть f(x) — многочлен над полем вещественных чисел f(x) 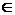 R[x]; α
R[x]; α 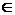 C(комплексное число). Если α — корень f(x), то и
C(комплексное число). Если α — корень f(x), то и 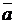 — корень f(x). Если α — корень кратности k, то и
— корень f(x). Если α — корень кратности k, то и 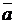 — корень кратности k ( α называют корнем кратности k многочлена, если f(x) можно представить в виде:
— корень кратности k ( α называют корнем кратности k многочлена, если f(x) можно представить в виде:
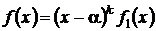 , где
, где 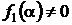 .
.
Доказательство. Пусть
f(x) =an xn +…a0 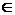 R[x], тогда
R[x], тогда
………………..
f(α)=anαn+an-1 αn-1+…+a0 =0
_ _
Отсюда следует, что
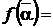 an(
an( 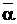 )n + an-1(
)n + an-1( 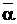 )n-1 +…+ a0
)n-1 +…+ a0 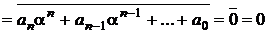 .
.
Пусть α — корень кратности k (α — комплексное число, 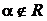 ), т.е.
), т.е. 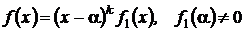 ,
, 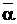 — корень какой-то кратности
— корень какой-то кратности 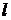 , т.е.
, т.е.
f(x) = (x- 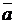 )l f2(x).
)l f2(x).
Докажем, что k=l.
Будем доказывать от противного, т.е. полагаем 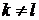 , например,
, например, 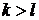 . Заметим, что α — корень f2(x), причем α — корень кратности k. Положим
. Заметим, что α — корень f2(x), причем α — корень кратности k. Положим
p(x)=(x-α) (x- 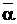 )=x2 + px +q
)=x2 + px +q 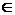 R[x]. Имеем
R[x]. Имеем
f(x)= (x-α)l(x-α)l q(x) = (x2+px+q)l q(x).
Отсюда следует, что q(x) — многочлен с действительными коэффициентами и q(α) = 0, ибо мы предположили, что k>l. Отсюда сразу же следует, что q( 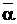 )=0. А это противоречит тому, что
)=0. А это противоречит тому, что 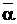 — корень кратности l. Пришли к противоречию. Оно возникло из предположения, что k>l. Аналогично получим противоречие, если предположим, что k<l.►
— корень кратности l. Пришли к противоречию. Оно возникло из предположения, что k>l. Аналогично получим противоречие, если предположим, что k<l.►
Следствие 3: Пусть f(x) 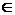 R[x] многочлен с действительными коэффициентами, f(x) можно представить в виде произведения его старшего коэффициента, линейных множителей вида (x-α), где α соответствует действительным корням многочлена, и множителей вида x2+px+q, соответствующих парам комплексно-сопряженных корней.
R[x] многочлен с действительными коэффициентами, f(x) можно представить в виде произведения его старшего коэффициента, линейных множителей вида (x-α), где α соответствует действительным корням многочлена, и множителей вида x2+px+q, соответствующих парам комплексно-сопряженных корней.
◄Cогласно следствию 1 f(x) можно представить в виде:
f(x) = a (x-α1)…(x-αk)(x-αk+1)(x-αk+1)…
Сначала запишем множители, соответствующие действительным корням, потом — множители, соответствующие парам комплексно-сопряженных корней.
Легко заметить, что многочлен (x-αk+1)(x- 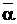 k+1)=x2+p1x+q1
k+1)=x2+p1x+q1 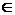 R[x] с действительными коэффициентами и так для каждой пары комплексно-сопряженных корней.
R[x] с действительными коэффициентами и так для каждой пары комплексно-сопряженных корней.
Замечание 2. Следствие 3 решает задачу о разложении на неприводимые над полем действительных чисел.
