Матрицы, Сложение и умножение на число

Матрица – математический объект вида таблицы, имеющий mстрок и nстолбцов.

Элементами матрицы могут быть как числа, так и функции.

Матрица может быть квадратной. В таком случае m=n.

В матрице есть главная диагональ – слева направо и, аналогично, побочная.

Матрица может быть треугольной – все элементы ниже\выше главной диагонали равны нули.

Матрица может быть диагональной – только элементы главной диагонали не равны нулю.

Матрица может быть единичной – все элементы главной диагонали диагональной матрицы равны единице.

Матрица может быть нулевой.

Матрицы можно:

· Сравнивать

Матрицы равны, если равны их размерности и содержимое.

· Складывать (сумма)

Складывать можно только матрицы одной размерности, в таком случае складываются элементы одного индекса.

Свойства суммы:

§ A+B=B+A

§ (A+B)+C=A+(B+C)

§ Для матрицы A(m,n) существует такая матрица 0(m,n), что A+0=A

· Умножать на число

В данном случае каждое из чисел матрицы умножается на число.

Свойства:

§ bcA=b(cA)

§ b(A+C)=bA+bC

§ A(b+c)=Ab+Ac

· Умножать на матрицу (рассматривается в следующем пункте).

Умножение матриц

При умножении матрицы Aна матрицу Bнеобходимо, чтобы число столбцов матрицы Aсовпадало с числом строк матрицы B. Только тогда можно умножать.

В таком случае результирующая матрица Cбудет иметь количество строк Aи столбцов B, а её числа будут результатом всех возможных перемножений строк Aна B.

Свойства:

§

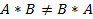
Бывают исключения, называемые коммутирующими матрицами.

§

§

§

§

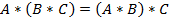
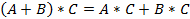
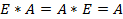
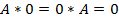
§ Det(A*B)=DetA*DetB

Обратная матрица

Матрица 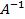называется обратной к матрице A, если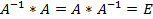

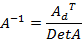
Где A_d^T– алгебраическое дополнение, транспонированное.

Примечание: алгебраическим дополнением для какого-либо элемента матрицы является определитель исходной матрицы свычеркнутыми строкой и столбцом исходной матрицы, в которых стоял данный элемент.

Теорема: для того, чтобы для матрицы существовала обратная, необходимо и достаточно, чтобы матрица имела определитель не равный нулю.

Док-во необходимости:

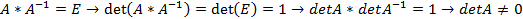
Док-во достаточности(док-во неверно!):

Пускай, B – алгебраическое дополнение матрицы A. ДомножимB на определитель A в минус первой степени.

Докажем, что .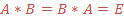

В таком случае, если вынести у B за скобку определитель в минус первой степени, то при произведении матриц мы получим на главной диагонали определители, а на всех остальных местах нули. Доможив на определитель, получим единичную матрицу.

Свойства обратной матрицы:

·

·

·

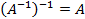
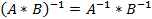
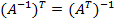
Ранг матрицы

Наибольший порядок не равного нулю минора матрицы Aназывается рангом матрицы A.

Ранг не может превышать наименьшее из числа строк\столбцов матрицы.

СЛАУ, методы решения.

Система Линейных Алгебраических Уравнений (СЛАУ) может быть:

· Однородной (все свободные члены равны нулю) и Неоднородной.

· Совместной (система имеет одно или более решений) и Несовместной.

· Определённой (одно решение) и Неопределённой.

· Если решения двух систем одинаковы, то они называются Эквивалентными.

Матричный метод

В матричном методе любое СЛАУ представляется, как матричное уравнение 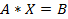, где A–матрица коэффициентов, X–искомая матрица неизвестных и B–матрица свободных коэффициентов.

Таким образом, .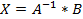

Метод Крамера

Метод (или же правило) Крамера – следствие из матричного метода.

Здесь каждый из неизвестных аргументов представляется собой как определитель аргумента поделённый на определитель матрицы СЛАУ, где определитель аргумента – определитель матрицы СЛАУ, в который столбец, принадлежащий искомому аргументу, был заменён на столбец свободных коэффициентов.

Метод Гаусса

Метод Гаусса использует элементарные преобразования строк для получения из расширенной матрицы СЛАУ треугольной или диагональной расширенной матрицы СЛАУ, которая при домножении на матрицу неизвестных аргументов даёт решение.