Алгебраические дополнения. Миноры. Формулы разложения определителя по столбцу или строке
Рассмотрим определитель матрицы
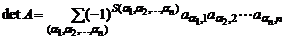 .
.
Выделим в этом определителе произвольный элемент 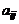 , соберем в правой части равенства все члены определителя, в которые входит
, соберем в правой части равенства все члены определителя, в которые входит 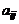 , и вынесем этот элемент за скобки. Величина
, и вынесем этот элемент за скобки. Величина 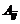 , стоящая в скобках, называется алгебраическим дополнением элемента
, стоящая в скобках, называется алгебраическим дополнением элемента 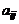 в определителе
в определителе 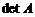 .
.
Например, в определителе третьего порядка алгебраическое дополнение элемента 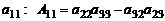 , а элемента
, а элемента 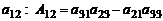 .
.
Так как в каждый член определителя входит один и только один элемент 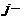 го столбца, то можно записать, что
го столбца, то можно записать, что
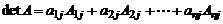 .
.
Это соотношение называется формулой разложения определителя по элементам 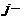 го столбца. Аналогичная формула записывается и для любой
го столбца. Аналогичная формула записывается и для любой 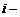 й строки
й строки
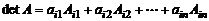 .
.
Рассмотрим теперь квадратную матрицу 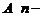 го порядка
го порядка
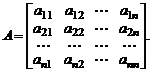
Выделим в этой матрице произвольные  строк с номерами
строк с номерами 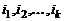 и столько же столбцов с номерами
и столько же столбцов с номерами 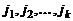 .Элементы, стоящие на пересечении выбранных строк и столбцов образуют квадратную матрицу
.Элементы, стоящие на пересечении выбранных строк и столбцов образуют квадратную матрицу 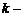 го порядка. Ее определитель называется минором
го порядка. Ее определитель называется минором 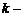 го порядка матрицы
го порядка матрицы 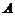 и обозначается
и обозначается 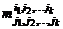 . Всякий элемент по определению есть минор 1-го порядка, а
. Всякий элемент по определению есть минор 1-го порядка, а 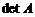 есть минор
есть минор 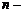 го порядка.
го порядка.
Если в исходной матрице зачеркнуть 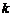 строк с номерами
строк с номерами 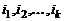 и
и 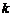 столбцов с номерами
столбцов с номерами 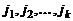 , то оставшиеся элементы образуют квадратную матрицу порядка
, то оставшиеся элементы образуют квадратную матрицу порядка 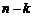 .Определитель этой матрицы
.Определитель этой матрицы 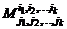 называется дополнительным минором для минора
называется дополнительным минором для минора 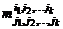 . Дополнительный минор к элементу
. Дополнительный минор к элементу 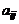 обозначается
обозначается 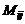 .
.
Например, в матрице
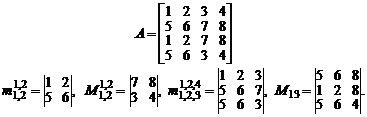
Миноры 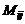 и алгебраические дополнения
и алгебраические дополнения 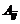 связаны между собой следующим равенством:
связаны между собой следующим равенством: 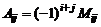 Из формул разложения определителя по строке или столбцу получаем, что
Из формул разложения определителя по строке или столбцу получаем, что
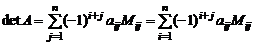 .
.
Обобщением этих формул является теорема Лапласа. Пусть в определителе 
 го порядка выделены любые
го порядка выделены любые 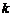 столбцов с номерами
столбцов с номерами 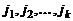 . Составим всевозможные миноры
. Составим всевозможные миноры 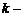 го порядка из элементов, находящихся на пересечении этих столбцов и произвольных
го порядка из элементов, находящихся на пересечении этих столбцов и произвольных 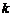 строк определителя с номерами
строк определителя с номерами 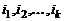 (
( 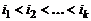 ). Тогда
). Тогда
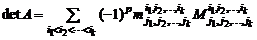 ,
,
где 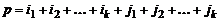 . Аналогичное разложение можно записать и для произвольных
. Аналогичное разложение можно записать и для произвольных 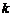 строк определителя
строк определителя
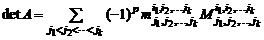 .
.
Вычисление определителей
Основным приемом вычисления определителя  го порядка является сведение его к определителям более низкого порядка с помощью формул разложения. При этом полезен учет свойств определителя, позволяющий существенно уменьшить объем вычислений.
го порядка является сведение его к определителям более низкого порядка с помощью формул разложения. При этом полезен учет свойств определителя, позволяющий существенно уменьшить объем вычислений.
Пример 1. Вычислить определитель
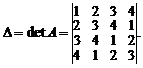
Разложим определитель по первому столбцу. Получим
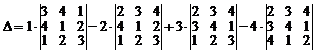 .
.
Таким образом, вычисление определителя четвертого порядка свелось к вычислению четырех определителей третьего порядка. Далее, разлагая определители третьего порядка по первому столбцу, получим
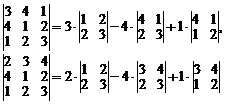
и т.д. Окончательно получим 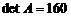 .
.
Вычисления значительно упростятся, если воспользоваться свойствами определителя. По свойству 7 можно, не меняя значения определителя, прибавить второй, третий и четвертый столбцы к первому, а затем первую строку вычесть из второй, третьей и четвертой. Получим
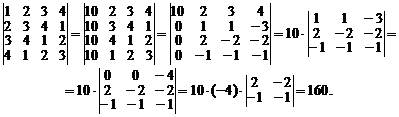
Пример 2. Вычислить определитель треугольной матрицы 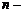 го порядка
го порядка
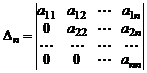 .
.
Для вычисления разложим определитель по последней строке. Получим, что 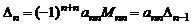 , где
, где 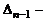 треугольный определитель порядка
треугольный определитель порядка 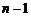 . Определитель
. Определитель 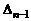 снова разложим по последней строке и т.д. Продолжая аналогичные рассуждения, получим что
снова разложим по последней строке и т.д. Продолжая аналогичные рассуждения, получим что 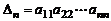 .
.
Пример 3. Вычислить определитель матрицы 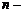 го порядка
го порядка
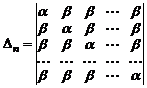 .
.
Подобные определители можно достаточно просто преобразовать к треугольному виду. Для этого прибавим все столбцы к первому и затем вычтем первую строку из всех остальных. Получим
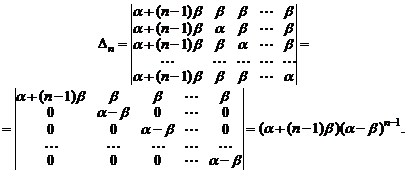
Пример 4. Следующий метод вычисления определителей  го порядка называется методом рекуррентных соотношений. Этот метод заключается в том, что данный определитель выражают, преобразуя его и раскладывая по строке или столбцу, через определители того же вида, но более низкого порядка. Полученное равенство называется рекуррентным соотношением.
го порядка называется методом рекуррентных соотношений. Этот метод заключается в том, что данный определитель выражают, преобразуя его и раскладывая по строке или столбцу, через определители того же вида, но более низкого порядка. Полученное равенство называется рекуррентным соотношением.
Рассмотрим идею метода на примере вычисления определителя трехдиагональной матрицы или матрицы Якоби (матрицей Якоби называется матрица 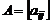 , если из
, если из 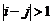 следует
следует 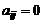 ). Вычисление определителей матриц Якоби часто приводит к рекуррентному соотношению вида
). Вычисление определителей матриц Якоби часто приводит к рекуррентному соотношению вида
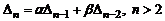 ,
,
где 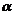 и
и 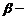 постоянные числа. Для нахождения
постоянные числа. Для нахождения 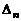 необходимо решить полученное уравнение. Заменим
необходимо решить полученное уравнение. Заменим 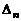 соответствующей степенью переменной
соответствующей степенью переменной 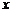
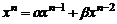 .
.
Перенося все слагаемые в левую часть и сокращая на 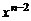 , получим квадратное уравнение
, получим квадратное уравнение 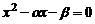 , называемое характеристическим уравнением. Пусть
, называемое характеристическим уравнением. Пусть 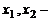 корни этого уравнения. Тогда возможны два случая:
корни этого уравнения. Тогда возможны два случая: 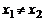 и
и 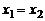 .
.
Если 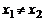 , то определитель
, то определитель  имеет вид
имеет вид
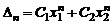 ,
,
где числа 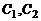 находятся из условий
находятся из условий
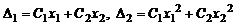 .
.
Определители 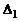 и
и 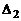 в левых частях условий вычисляются непосредственно из вида
в левых частях условий вычисляются непосредственно из вида 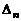 .
.
Если 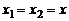 , то
, то
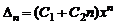 ,
,
а числа 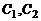 находятся из условий
находятся из условий
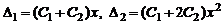 .
.
Рассмотрим конкретный пример. Вычислим определитель 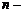 го порядка
го порядка
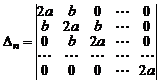 ,
,  .
.
Разложим определитель по последнему столбцу
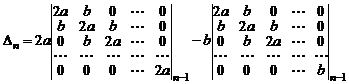 .
.
Первый определитель в правой части является определителем порядка 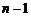 того же типа, что и
того же типа, что и 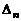 . Второй определитель разложим еще раз по последней строке. Минор, дополнительный к ненулевому элементу в последней строке, вновь представляет собой определитель того же типа, что и
. Второй определитель разложим еще раз по последней строке. Минор, дополнительный к ненулевому элементу в последней строке, вновь представляет собой определитель того же типа, что и 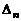 , но порядка
, но порядка 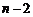 . В итоге получим рекуррентное соотношение для
. В итоге получим рекуррентное соотношение для 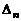
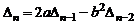 .
.
Соответствующее характеристическое уравнение
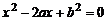
имеет корни 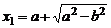 и
и 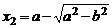 . Так как
. Так как 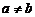 , то
, то 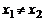 и
и 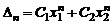 . Из вида
. Из вида 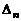 находим
находим
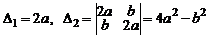 .
.
Тогда для определения 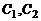 получим систему уравнений
получим систему уравнений

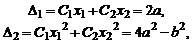
решая которую, находим
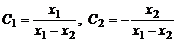
(при решении использовались равенства: 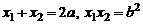 ). Тогда
). Тогда
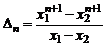 .
.
Пример 5. Вычислить определитель 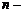 го порядка
го порядка
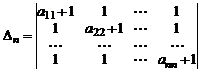 .
.
Представим элементы последнего столбца в виде суммы двух слагаемых: 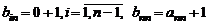 . Тогда по свойству 3. определитель представится в виде суммы двух определителей
. Тогда по свойству 3. определитель представится в виде суммы двух определителей
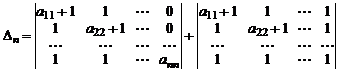 .
.
Первый определитель разложим по последнему столбцу. Второй определитель приведем к треугольному виду, вычитая последний столбец из всех остальных. Тогда
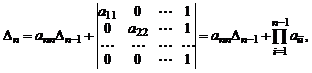 (1)
(1)
где 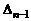 является определителем порядка
является определителем порядка 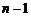 того же типа, что и
того же типа, что и 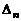 .
.
Решим полученное уравнение для 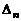 . Из вида
. Из вида 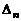 при
при 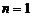 имеем
имеем 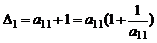 .Выписывая (1) при
.Выписывая (1) при 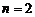 с учетом равенства для
с учетом равенства для 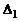 , получаем
, получаем
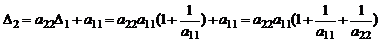 .
.
Методом математической индукции теперь нетрудно показать, что 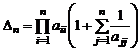 .
.
Пример 6.Вычислить определитель 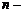 го порядка
го порядка
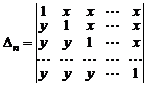 .
.
Представим элементы последнего столбца в виде суммы двух слагаемых: 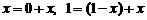 и распишем определитель как сумму двух определителей
и распишем определитель как сумму двух определителей
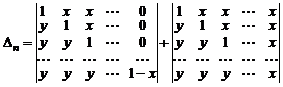 .
.
Первый определитель разложим по последнему столбцу. Для вычисления второго определителя умножим последний столбец на 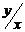 и вычтем из остальных. Получим
и вычтем из остальных. Получим
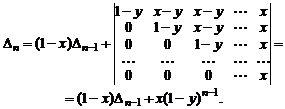
Для решения полученного рекуррентного соотношения воспользуемся тем, что при транспонировании матрицы ее определитель не меняется. В нашем случае транспонировании приводит к замене 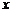 на
на 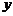 наоборот. Поэтому имеем два равенства
наоборот. Поэтому имеем два равенства
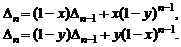
Откуда 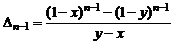 .
.
Пример 7.Следующий пример иллюстрирует применение теоремы Лапласа. Нужно вычислить определитель квазитреугольной матрицы порядка 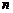 . Квазитреугольной называют блочную матрицу вида
. Квазитреугольной называют блочную матрицу вида 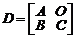 , где
, где 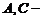 квадратные матрицы,
квадратные матрицы, 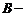 прямоугольная матрица,
прямоугольная матрица, 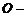 нулевая матрица. В подробной записи матрица имеет вид
нулевая матрица. В подробной записи матрица имеет вид
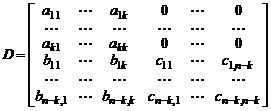 .
.
Пусть 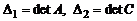 . Покажем, что
. Покажем, что 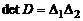 . Воспользуемся теоремой Лапласа. Разложим этот определитель по первым
. Воспользуемся теоремой Лапласа. Разложим этот определитель по первым 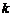 строкам. Очевидно, что из первых
строкам. Очевидно, что из первых 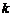 строк можно составить только один минор
строк можно составить только один минор 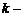 го порядка не содержащий нулевого столбца, у которого номера выделяемых столбцов удовлетворяют условию
го порядка не содержащий нулевого столбца, у которого номера выделяемых столбцов удовлетворяют условию 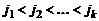 . Этот минор есть
. Этот минор есть 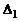 . Дополнительным к нему минором является определитель
. Дополнительным к нему минором является определитель 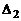 , что и доказывает формулу.
, что и доказывает формулу.
Задачи
1. Определить число инверсий в перестановках:
а) 1,9.6,3.2.4.7.8.
б) 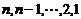 .
.
в) 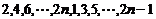 .
.
2. Выбрать значения 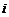 и
и 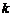 так, чтобы произведение
так, чтобы произведение 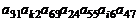 входило в определитель 7-го порядка со знаком плюс.
входило в определитель 7-го порядка со знаком плюс.
3. С каким знаком входит в определитель порядка 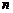 произведение элементов побочной диагонали?
произведение элементов побочной диагонали?
4. Найти члены определителя
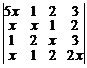 ,
,
содержащие 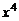 и
и 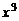 .
.
5. Пользуясь только определением, вычислить определитель
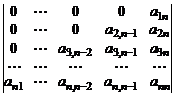 .
.
6. Пользуясь только свойствами определителей вычислить следующие определители:
а) 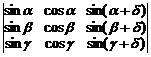 . б)
. б) 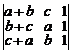 .
.
в) 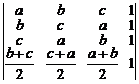 . г)
. г) 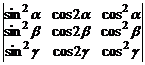 .
.
д) 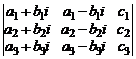 , где
, где 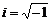 .
.
7. Не вычисляя определителей, доказать следующие тождества:
а) 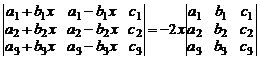 .
.
б) 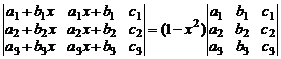 .
.
в) 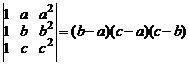 .
.
г) 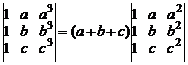 .
.
8. Пользуясь свойствами определителей, включая разложение по строке или столбцу, доказать тождество:
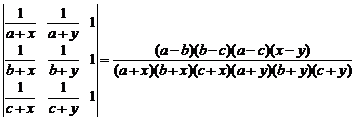 .
.
9. Разлагая по 2-му столбцу, вычислить определитель
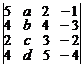 .
.
Вычислить определители:
10.  . 11.
. 11. 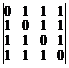 . 12.
. 12. 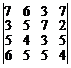 .
.
13. 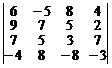 . 14.
. 14. 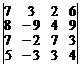 .
.
15. 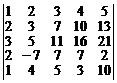 . 16.
. 16. 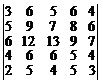 .
.
В следующих задачах, где по виду определителя нельзя установить его порядок, предполагается, что он равен 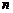 .
.
Вычислить следующие определители, приводя их к треугольному виду.
17. 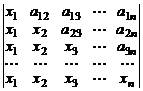 . 18.
. 18. 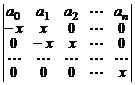 .
.
19. 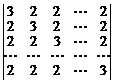 20.
20. 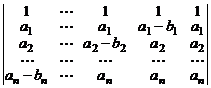 .
.
Вычислить следующие определители методом рекуррентных соотношений.
21. 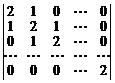 22.
22. 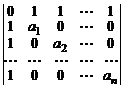 .
.
23. 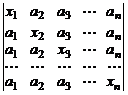 . 24.
. 24. 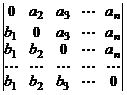 .
.
Пользуясь теоремой Лапласа вычислить следующие определители.
25. 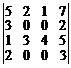 . 26.
. 26. 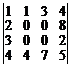 . 27.
. 27. 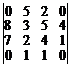 .
.
28. 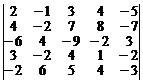 . 29.
. 29. 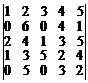 .
.
Вычислить определители:
30. 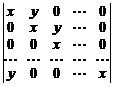 . 31.
. 31. 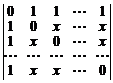 .
.
32.  . 33.
. 33. 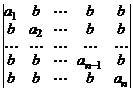 .
.
34. 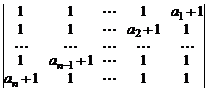 .
.
35. 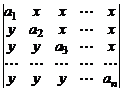 . 36.
. 36. 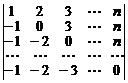 .
.
37. Порядок следующего определителя равен 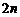 :
:
 .
.
38.  .
.
39. 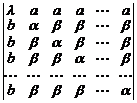 . 40.
. 40. 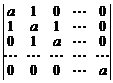 .
.
41.  .
.
42. 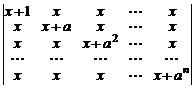 .
.
Обратная матрица
Квадратная матрица 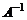 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице 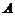 того же порядка, если
того же порядка, если
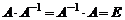 .
.
Необходимым и достаточным условием существования обратной матрицы является невырожденность матрицы 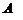 т.е.
т.е.
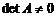 .
.
В этом случае обратная матрица существует, является единственной и определяется соотношением
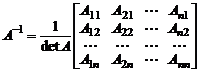 ,
,
где 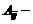 алгебраические дополнения элементов
алгебраические дополнения элементов 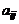 матрицы
матрицы 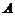 .
.
Обратная матрица обладает следующими свойствами:
1. 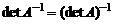 .
.
2. 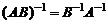 .
.
3. 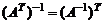 .
.
Полезно помнить, что если матрица 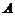 является треугольной, то
является треугольной, то 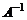 является треугольной того же типа, что и матрица
является треугольной того же типа, что и матрица 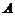 . Обратная к симметричной матрице тоже симметрична.
. Обратная к симметричной матрице тоже симметрична.
Пример. Найти матрицу обратную к матрице
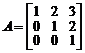 .
.
Определитель 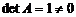 и, следовательно, обратная матрица существует. Алгебраические дополнения элементов матрицы
и, следовательно, обратная матрица существует. Алгебраические дополнения элементов матрицы 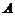 равны
равны
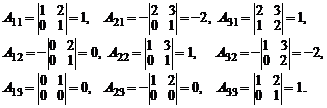
Поэтому
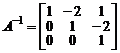 .
.
Задачи
Найти матрицы обратные к данным.
1. 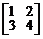 . 2.
. 2. 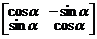 . 3.
. 3. 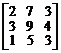 .
.
4. 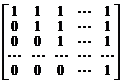 . 5.
. 5. 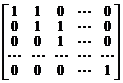 .
.
6.  .
.
7. Решить матричные уравнения:
а) 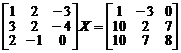 .
.
б) 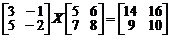 .
.
8. Показать, что вычисление матрицы, обратной к данной матрице порядка 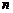 , можно свести к решению
, можно свести к решению 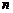 систем линейных уравнений, каждая из которых содержит
систем линейных уравнений, каждая из которых содержит 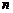 уравнений с
уравнений с 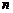 неизвестными и имеет матрицей коэффициентов при неизвестных матрицу
неизвестными и имеет матрицей коэффициентов при неизвестных матрицу 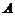 .
.
9. Как изменится обратная матрица 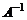 , если в данной матрице
, если в данной матрице 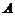 :
:
а) переставить 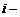 ю и
ю и  ю строки?
ю строки?
б)  ю строку умножить на число
ю строку умножить на число  ?
?
в) к  й строке прибавить
й строке прибавить 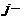 ю, умноженную на число
ю, умноженную на число 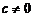 , или совершить аналогичное преобразование столбцов?
, или совершить аналогичное преобразование столбцов?
Ранг матрицы
Основные понятия
Определение 1. Пусть даны 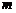 вектор – столбцов порядка
вектор – столбцов порядка 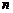
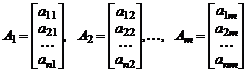
и 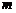 скаляров
скаляров 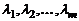 . Умножая
. Умножая 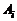 на
на 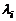 и складывая, получим вектор – столбец
и складывая, получим вектор – столбец 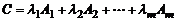 с элементами
с элементами 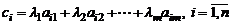 , который называется линейной комбинацией столбцов
, который называется линейной комбинацией столбцов 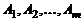 .
.
Определение 2. Столбцы 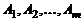 называются линейно зависимыми, если найдутся такие числа
называются линейно зависимыми, если найдутся такие числа 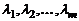 , не равные нулю одновременно, что линейная комбинация
, не равные нулю одновременно, что линейная комбинация
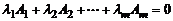 ,
,
где ноль справа это нулевой вектор – столбец.
Определение 3. Столбцы 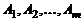 называются линейно независимыми, если равенство
называются линейно независимыми, если равенство
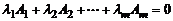
возможно только при условии 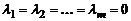 .
.
Необходимым и достаточным условием линейной зависимости вектор – столбцов является равенство одного из них линейной комбинации других.
Пример. Пусть даны вектор – столбцы
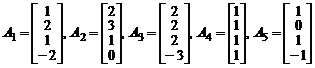 .
.
Нетрудно заметить, что столбец 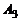 равен сумме
равен сумме 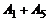 . Поэтому при
. Поэтому при 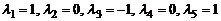 линейная комбинация данных столбцов равна нулю и, следовательно, они линейно зависимы.
линейная комбинация данных столбцов равна нулю и, следовательно, они линейно зависимы.
В общем случае проверка условия линейной зависимости сводится к нахождению ненулевого решения системы уравнений
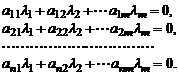
Рассмотрим теперь матрицу  порядка
порядка 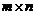 .
.
Определение 4. Натуральное число 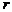 называется рангом матрицы
называется рангом матрицы 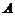 , если у нее имеется минор порядка
, если у нее имеется минор порядка 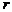 отличный от нуля, а все миноры порядка
отличный от нуля, а все миноры порядка 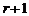 и выше, если это возможно, равны нулю. Очевидно, что
и выше, если это возможно, равны нулю. Очевидно, что 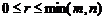 .
.
Определение 5. Если ранг матрицы равен 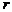 , то всякий отличный от нуля минор порядка
, то всякий отличный от нуля минор порядка 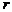 матрицы
матрицы  называется базисным минором. Строки и столбцы матрицы
называется базисным минором. Строки и столбцы матрицы  , на пересечении которых расположен базисный минор, называются базисными строками и столбцами.
, на пересечении которых расположен базисный минор, называются базисными строками и столбцами.
Теорема (о базисном миноре). Базисные столбцы (строки) матрицы линейно независимы. Любой столбец (любая строка) матрицы является линейной комбинацией базисных столбцов (строк).
Из последних утверждений следует второе определение ранга матрицы: ранг матрицы равен максимальному числу ее линейно независимых столбцов (строк).
Вычисление ранга матрицы
Вычисление ранга матрицы можно проводить одним из следующих способов.
Первый состоит в сведении данной матрицы с помощью элементарных преобразований к канонической матрице. Каноническая матрица является блочной матрицей, у которой один из блоков представляет собой единичную матрицу, а все остальные блоки – нулевые матрицы.
Каноническую матрицу можно записать в виде
 .
.
Ранг канонической матрицы равен, очевидно, числу единиц, стоящих на диагонали. Преобразования, не меняющие ранга матрицы, называются элементарными. К их числу относятся:
1. Перестановка двух любых столбцов (строк) матрицы.
2. Умножение столбца (строки) на отличное от нуля число.
3. Прибавление к одному столбцу (строке) линейной комбинации других столбцов (строк).
Пример. Вычислить ранг матрицы
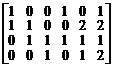 .
.
Вычтем первый столбец из четвертого и шестого, а в получившейся матрице второй столбец прибавим к четвертому, вычтем его из шестого, и удвоенный второй столбец вычтем из пятого:
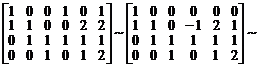
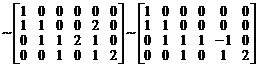 .
.
В полученной матрице третий столбец прибавим к пятому и вычтем из четвертого
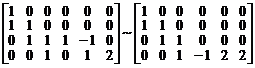 .
.
Далее, четвертый столбец прибавим к третьему, удвоенный четвертый столбец прибавим к пятому и шестому. Наконец, в полученной матрице вычтем третий столбец из второго, а получившийся второй из первого
 .
.
Ранг последней матрицы равен, очевидно, 4.
Второй способ вычисления матрицы дает метод окаймления миноров, основанный на следующей теореме:
Теорема. Пусть матрица 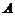 имеет минор
имеет минор 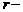 го порядка отличный от нуля, а все миноры
го порядка отличный от нуля, а все миноры 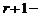 го порядка, содержащие (окаймляющие) его равны нулю. Тогда ранг матрицы
го порядка, содержащие (окаймляющие) его равны нулю. Тогда ранг матрицы 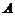 равен
равен 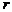 .
.
Пример. Вычислить ранг матрицы методом окаймления миноров
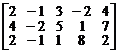 .
.
У матрицы имеется минор второго порядка 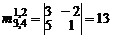 . Поэтому ранг данной матрицы не меньше двух. Окаймляют данный минор следующие миноры третьего порядка
. Поэтому ранг данной матрицы не меньше двух. Окаймляют данный минор следующие миноры третьего порядка
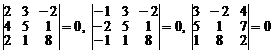 .
.
Так как все они равны нулю, ранг матрицы равен двум.
Задачи
Вычислить ранг следующих матриц методом окаймления миноров.
1. 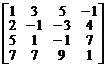 . 2.
. 2. 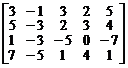 .
.
Вычислить ранг следующих матриц при помощи элементарных преобразований.
3. 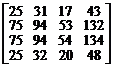 . 4.
. 4. 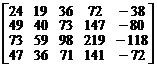 .
.
5. Чему равен ранг матрицы
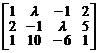
при различных значениях 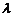 ?
?
6. Доказать, что система вектор – столбцов, содержащая нулевой вектор, линейно зависима.
7. Доказать, что если часть системы вектор – столбцов линейно зависима, то и вся система линейно зависима.
8. Найти все значения 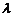 , при которых вектор – столбец
, при которых вектор – столбец 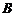 линейно выражается через вектор – столбцы
линейно выражается через вектор – столбцы 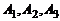 .
.
а) 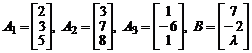 .
.
б) 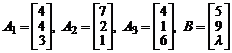 .
.
Системы линейных уравнений
5.1. Основные определения
Определение 1.Системой линейных уравнений относительно неизвестных 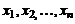 называется система уравнений вида
называется система уравнений вида
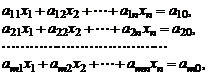
где 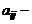 произвольные заданные числа – коэффициенты уравнений,
произвольные заданные числа – коэффициенты уравнений, 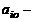 свободные члены.
свободные члены.
Если ввести матрицы
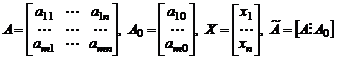 ,
,
то систему уравнений можно записать в матричном виде
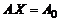 .
.
Матрица 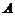 называется основной матрицей системы, матрица
называется основной матрицей системы, матрица 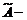 расширенной матрицей системы.
расширенной матрицей системы.
Если 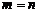 , то система называется квадратной. Если все
, то система называется квадратной. Если все 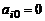 , система называется однородной.
, система называется однородной.
Определение 2.Решением системы линейных уравнений называется всякая совокупность 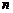 чисел
чисел 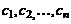 , которая при подстановке в систему вместо неизвестных
, которая при подстановке в систему вместо неизвестных 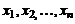 превращает систему уравнений в систему тождеств. Система, имеющая хотя бы одно решение, называется совместной (разрешимой).
превращает систему уравнений в систему тождеств. Система, имеющая хотя бы одно решение, называется совместной (разрешимой).
Определение 3.Всякое решение совместной системы называется ее частным решением. Совокупность всех частных решений называется общим решением.
Определение 4.Две системы уравнений называются эквивалентными, если каждое решение одной системы является решением другой.
В следующей теореме формулируется условие совместности системы линейных уравнений.
Теорема Кронекера – Копелли.Система линейных уравнений 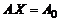 совместна тогда и только тогда, когда ранг расширенной матрицы
совместна тогда и только тогда, когда ранг расширенной матрицы 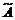 системы равен рангу основной матрицы
системы равен рангу основной матрицы 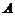 этой системы.
этой системы.
Теорема(о числе решений совместной системы). Всякая совместная система уравнений с 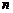 неизвестными ранга
неизвестными ранга 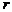 при
при 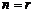 имеет единственное решение. Если
имеет единственное решение. Если 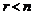 , то система имеет бесконечно много решений.
, то система имеет бесконечно много решений.
Выделим в основной матрице совместной системы базисный минор.
Определение 5. Уравнения системы, соответствующие базисным строкам матрицы, называются базисными уравнениями. Их совокупность называется базисной системой уравнений. Неизвестные, коэффициенты при которых образуют базисные столбцы матрицы системы, называются главными неизвестными, остальные – свободными.
Всякая линейная система эквивалентна системе своих базисных уравнений.
При решении линейной системы, прежде всего, выделяют базисную систему. Если базисная система является совместной и состоит из 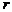 уравнений с
уравнений с 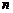 неизвестными, то далее
неизвестными, то далее 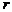 главных неизвестных выражают через
главных неизвестных выражают через 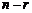 свободных.
свободных.
