Матрицы. системы линейных уравнений
МАТРИЦЫ. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Учебно-методическое пособие
Томск
РАССМОТРЕНО и УТВЕРЖДЕНО методической комиссией факультета прикладной математики и кибернетики.
ПРОТОКОЛ № 26 от 26 января 2007 г.
Председатель комиссии
профессор С.Э.Воробейчиков
В учебно-методическом пособии приведены краткие теоретические сведения и даны практические рекомендации к решению задач по курсу «Линейная алгебра и аналитическая геометрия».
Пособие разработано для студентов факультета прикладной математики и кибернетики дневной формы обучения.
Составители: К.И.Лившиц
Л.Ю.Сухотина
 |
1. Матрицы
Основные понятия
Определение.Пусть 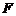 — множество чисел и
— множество чисел и 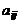 — набор из
— набор из 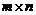 элементов множества
элементов множества 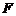 . Прямоугольная таблица
. Прямоугольная таблица
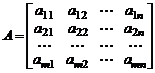 ,
,
состоящая из 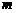 строк и
строк и 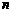 столбцов, называется матрицей.
столбцов, называется матрицей.
Числа 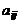 , входящие в состав данной матрицы, называются ее элементами. Совокупность элементов
, входящие в состав данной матрицы, называются ее элементами. Совокупность элементов 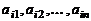 образуют
образуют 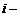 ю строку матрицы, а совокупность элементов
ю строку матрицы, а совокупность элементов 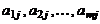 образует
образует 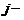 й столбец матрицы. Величины
й столбец матрицы. Величины 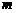 и
и 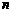 называются порядками матрицы.
называются порядками матрицы.
Две матрицы, имеющие одинаковое число 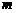 строк и одинаковое число
строк и одинаковое число 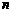 столбцов называются матрицами одинакового типа. Две матрицы
столбцов называются матрицами одинакового типа. Две матрицы 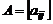 и
и 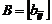 называются равными, если они имеют одинаковые порядки и
называются равными, если они имеют одинаковые порядки и 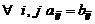 .
.
Если 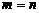 , матрица называется квадратной. Совокупность элементов
, матрица называется квадратной. Совокупность элементов 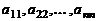 называется главной диагональю матрицы. Квадратная матрица, у которой отличны от нуля лишь элементы главной диагонали, называется диагональной. Если все диагональные элементы диагональной матрицы
называется главной диагональю матрицы. Квадратная матрица, у которой отличны от нуля лишь элементы главной диагонали, называется диагональной. Если все диагональные элементы диагональной матрицы 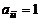 , то диагональная матрица называется единичной и обозначается символом
, то диагональная матрица называется единичной и обозначается символом 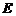 .
.
Матрица, у которой все элементы равны нулю, называется нулевой матрицей и обозначается 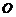 . Нулевые матрицы различных порядков считаются различными, так как состоят из разного числа элементов.
. Нулевые матрицы различных порядков считаются различными, так как состоят из разного числа элементов.
Квадратная матрица называется верхней треугольной, если из 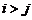 следует, что
следует, что 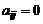 и нижней треугольной, если из
и нижней треугольной, если из 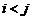 следует, что
следует, что 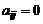 .
.
Матрицу, состоящую из одной строки, называют вектор — строкой, а матрицу, состоящую из одного столбца, называют вектор — столбцом. Например, матрица 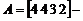 вектор — строка размера
вектор — строка размера 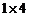 .
.
Действия с матрицами
1. Транспонирование матриц. Операция транспонирования матриц состоит в перемене местами строк и столбцов с сохранением их номеров. Пусть дана матрица 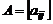 порядка
порядка 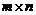 . Тогда транспонированной по отношению матрице
. Тогда транспонированной по отношению матрице 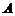 называется матрица
называется матрица 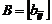 порядка
порядка 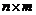 , элементы которой
, элементы которой 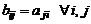 . Транспонирование матрицы обозначается как
. Транспонирование матрицы обозначается как 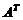 .
.
Пример. Пусть 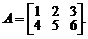 Тогда
Тогда 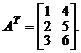
2. Сложение матриц.Операция сложения вводится только для матриц одинакового типа. Суммой двух матриц 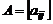 и
и 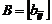 одинакового типа называется матрица
одинакового типа называется матрица 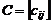 того же типа, элементы которой
того же типа, элементы которой 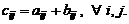 Используется обозначение
Используется обозначение 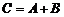 .
.
3. Умножение матрицы на число.Произведением матрицы 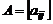 порядка
порядка 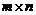 и числа
и числа 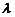 называется матрица
называется матрица 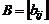 того же типа, элементы которой
того же типа, элементы которой 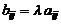 . Используется обозначение
. Используется обозначение 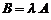 .
.
Пример.Пусть 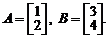
Тогда матрица 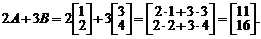
4. Умножение матрицы на матрицу. Операция умножения матрицы 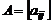 на матрицу
на матрицу 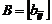 вводится для прямоугольных матриц при условии, что число столбцов матрицы
вводится для прямоугольных матриц при условии, что число столбцов матрицы 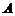 равно числу строк матрицы
равно числу строк матрицы 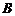 . Произведением матрицы
. Произведением матрицы 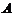 порядка
порядка 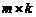 и матрицы
и матрицы 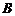 порядка
порядка 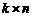 , заданных в определенном порядке (
, заданных в определенном порядке ( 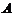 — первая,
— первая, 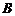 — вторая), называется матрица
— вторая), называется матрица 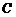 порядка
порядка 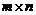 , элементы которой
, элементы которой
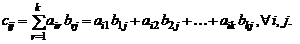
Таким образом, элемент 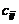 матрицы
матрицы 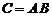 есть сумма произведений элементов
есть сумма произведений элементов 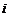 - й строки матрицы
- й строки матрицы 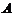 на соответствующие элементы
на соответствующие элементы 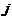 - го столбца матрицы
- го столбца матрицы 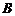 .
.
Пример 1. Пусть 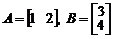 . Тогда
. Тогда
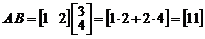 ,
,
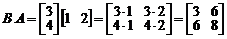 .
.
Пример 2.Пусть 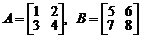 . Тогда
. Тогда
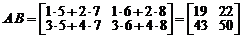 .
.
Задачи
Вычислить произведения матриц:
1. 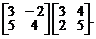 2.
2. 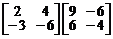 . 3.
. 3. 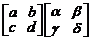 .
.
4. 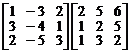 . 5.
. 5. 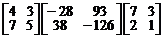 .
.
6. Доказать, что если для матриц 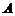 и
и 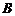 оба произведения
оба произведения 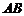 и
и 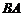 существуют, причем
существуют, причем 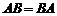 , то матрицы
, то матрицы 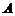 и
и 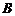 - квадратные и имеют одинаковый порядок.
- квадратные и имеют одинаковый порядок.
Вычислить выражения:
7. 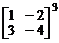 . 8.
. 8. 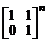 . 9.
. 9. 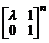 .
.
10.  , порядок матрицы равен
, порядок матрицы равен 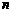 .
.
11. Найти значение многочлена 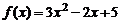 от матрицы
от матрицы 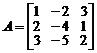 .
.
12. Доказать, что если матрицы 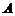 и
и 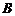 - квадратные и имеют одинаковый порядок, причем
- квадратные и имеют одинаковый порядок, причем 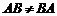 , то
, то
а) 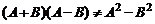 . б)
. б) 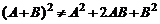 .
.
13. Доказать, что если матрицы 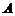 и
и 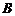 - квадратные и имеют одинаковый порядок, причем
- квадратные и имеют одинаковый порядок, причем 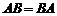 , то
, то
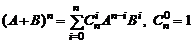 .
.
14. Найти все матрицы, перестановочные с матрицей
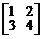 .
.
Определители
Основные понятия
Понятие определителя вводится только для квадратных матриц. Пусть 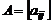 — квадратная матрица порядка
— квадратная матрица порядка 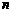 . Составим произведение из
. Составим произведение из 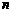 различных элементов матрицы
различных элементов матрицы 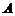 , выбирая по одному и только одному элементу из каждой строки и каждого столбца. Запишем это произведение в виде
, выбирая по одному и только одному элементу из каждой строки и каждого столбца. Запишем это произведение в виде 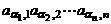 . Будем называть его членом определителя. Рассмотрим последовательность чисел
. Будем называть его членом определителя. Рассмотрим последовательность чисел 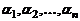 . По самому построению члена определителя это различные числа, которые представляют собой перестановку чисел от 1 до
. По самому построению члена определителя это различные числа, которые представляют собой перестановку чисел от 1 до 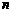 . Назовем инверсией в перестановке
. Назовем инверсией в перестановке 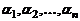 такое расположение чисел, когда старшее стоит перед младшим. Например, в перестановке 1,2,4,5,7,9,10,8,3,6 будет 12 инверсий. Обозначим число инверсий в перестановке через
такое расположение чисел, когда старшее стоит перед младшим. Например, в перестановке 1,2,4,5,7,9,10,8,3,6 будет 12 инверсий. Обозначим число инверсий в перестановке через 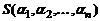 . Так как из
. Так как из 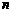 чисел можно составить
чисел можно составить 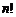 различных перестановок, то число различных членов определителя равно
различных перестановок, то число различных членов определителя равно 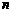 !
!
Определение. Определителем (детерминантом) матрицы 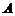 называется алгебраическая сумма
называется алгебраическая сумма 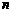 ! членов определителя перед каждым из которых стоит знак
! членов определителя перед каждым из которых стоит знак 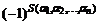 . Или
. Или
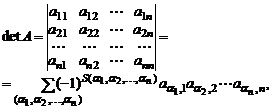
где сумма берется по всем возможным перестановкам 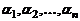 .
.
Хотя определитель матрицы это число, будем для удобства столбцы и строки матрицы 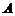 называть также столбцами и строками ее определителя
называть также столбцами и строками ее определителя 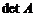 .
.
Пример. Вычислим определитель матрицы второго порядка
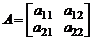 .
.
Члены определителя имеют вид 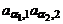 , где
, где 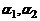 принимают значения 1 и 2. Возможны две пары значений
принимают значения 1 и 2. Возможны две пары значений 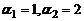 и
и 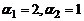 . Поэтому
. Поэтому
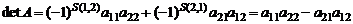 .
.
Свойства определителя
1. При транспонировании матрицы ее определитель не меняется, т.е. 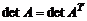 . Поэтому свойства, сформулированные для столбцов матрицы, справедливы и для строк.
. Поэтому свойства, сформулированные для столбцов матрицы, справедливы и для строк.
2. При перестановке двух столбцов (строк) матрицы ее определитель меняет знак на противоположный.
3. Обозначим через 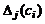 определитель,
определитель, 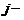 й столбец которого есть вектор-столбец
й столбец которого есть вектор-столбец 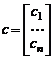 . Если все элементы
. Если все элементы 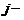 го столбца определителя представлены в виде линейной комбинации двух слагаемых
го столбца определителя представлены в виде линейной комбинации двух слагаемых 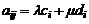 , где
, где 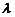 и
и 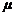 фиксированные числа, то определитель равен линейной комбинации двух определителей
фиксированные числа, то определитель равен линейной комбинации двух определителей
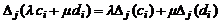 .
.
Например,
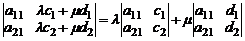 .
.
4. Определитель матрицы с двумя одинаковыми столбцами равен нулю.
6. Если некоторый столбец матрицы состоит из нулей, то определитель этой матрицы равен нулю.
7. Если к элементам одного столбца определителя прибавить соответствующие элементы другого столбца, умноженные на одно и то же число, то определитель не изменится. Например,
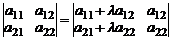 .
.
Вычисление определителей
Основным приемом вычисления определителя 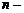 го порядка является сведение его к определителям более низкого порядка с помощью формул разложения. При этом полезен учет свойств определителя, позволяющий существенно уменьшить объем вычислений.
го порядка является сведение его к определителям более низкого порядка с помощью формул разложения. При этом полезен учет свойств определителя, позволяющий существенно уменьшить объем вычислений.
Пример 1. Вычислить определитель
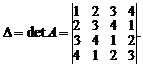
Разложим определитель по первому столбцу. Получим
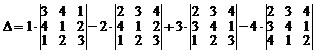 .
.
Таким образом, вычисление определителя четвертого порядка свелось к вычислению четырех определителей третьего порядка. Далее, разлагая определители третьего порядка по первому столбцу, получим
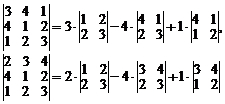
и т.д. Окончательно получим 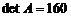 .
.
Вычисления значительно упростятся, если воспользоваться свойствами определителя. По свойству 7 можно, не меняя значения определителя, прибавить второй, третий и четвертый столбцы к первому, а затем первую строку вычесть из второй, третьей и четвертой. Получим
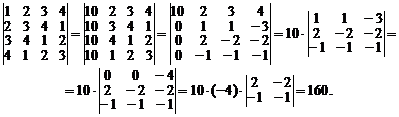
Пример 2. Вычислить определитель треугольной матрицы 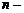 го порядка
го порядка
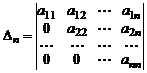 .
.
Для вычисления разложим определитель по последней строке. Получим, что 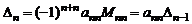 , где
, где 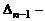 треугольный определитель порядка
треугольный определитель порядка 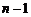 . Определитель
. Определитель 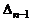 снова разложим по последней строке и т.д. Продолжая аналогичные рассуждения, получим что
снова разложим по последней строке и т.д. Продолжая аналогичные рассуждения, получим что 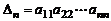 .
.
Пример 3. Вычислить определитель матрицы 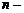 го порядка
го порядка
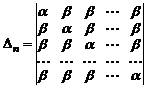 .
.
Подобные определители можно достаточно просто преобразовать к треугольному виду. Для этого прибавим все столбцы к первому и затем вычтем первую строку из всех остальных. Получим
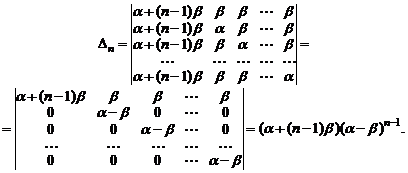
Пример 4. Следующий метод вычисления определителей 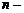 го порядка называется методом рекуррентных соотношений. Этот метод заключается в том, что данный определитель выражают, преобразуя его и раскладывая по строке или столбцу, через определители того же вида, но более низкого порядка. Полученное равенство называется рекуррентным соотношением.
го порядка называется методом рекуррентных соотношений. Этот метод заключается в том, что данный определитель выражают, преобразуя его и раскладывая по строке или столбцу, через определители того же вида, но более низкого порядка. Полученное равенство называется рекуррентным соотношением.
Рассмотрим идею метода на примере вычисления определителя трехдиагональной матрицы или матрицы Якоби (матрицей Якоби называется матрица 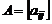 , если из
, если из 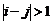 следует
следует 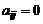 ). Вычисление определителей матриц Якоби часто приводит к рекуррентному соотношению вида
). Вычисление определителей матриц Якоби часто приводит к рекуррентному соотношению вида
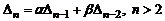 ,
,
где 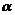 и
и 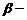 постоянные числа. Для нахождения
постоянные числа. Для нахождения 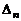 необходимо решить полученное уравнение. Заменим
необходимо решить полученное уравнение. Заменим 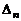 соответствующей степенью переменной
соответствующей степенью переменной 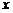
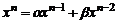 .
.
Перенося все слагаемые в левую часть и сокращая на 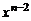 , получим квадратное уравнение
, получим квадратное уравнение 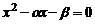 , называемое характеристическим уравнением. Пусть
, называемое характеристическим уравнением. Пусть 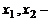 корни этого уравнения. Тогда возможны два случая:
корни этого уравнения. Тогда возможны два случая: 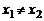 и
и 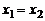 .
.
Если 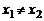 , то определитель
, то определитель 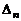 имеет вид
имеет вид
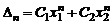 ,
,
где числа 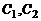 находятся из условий
находятся из условий
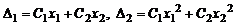 .
.
Определители 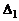 и
и 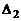 в левых частях условий вычисляются непосредственно из вида
в левых частях условий вычисляются непосредственно из вида 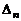 .
.
Если 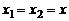 , то
, то
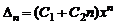 ,
,
а числа 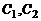 находятся из условий
находятся из условий
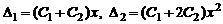 .
.
Рассмотрим конкретный пример. Вычислим определитель 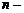 го порядка
го порядка
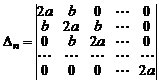 ,
, 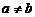 .
.
Разложим определитель по последнему столбцу
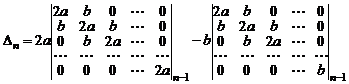 .
.
Первый определитель в правой части является определителем порядка 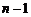 того же типа, что и
того же типа, что и 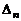 . Второй определитель разложим еще раз по последней строке. Минор, дополнительный к ненулевому элементу в последней строке, вновь представляет собой определитель того же типа, что и
. Второй определитель разложим еще раз по последней строке. Минор, дополнительный к ненулевому элементу в последней строке, вновь представляет собой определитель того же типа, что и 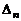 , но порядка
, но порядка 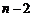 . В итоге получим рекуррентное соотношение для
. В итоге получим рекуррентное соотношение для 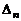
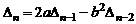 .
.
Соответствующее характеристическое уравнение
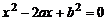
имеет корни 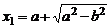 и
и 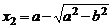 . Так как
. Так как 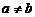 , то
, то 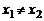 и
и 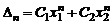 . Из вида
. Из вида 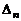 находим
находим
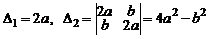 .
.
Тогда для определения 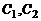 получим систему уравнений
получим систему уравнений

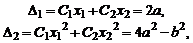
решая которую, находим
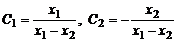
(при решении использовались равенства: 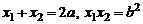 ). Тогда
). Тогда
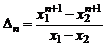 .
.
Пример 5. Вычислить определитель 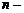 го порядка
го порядка
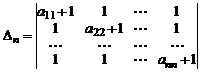 .
.
Представим элементы последнего столбца в виде суммы двух слагаемых: 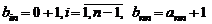 . Тогда по свойству 3. определитель представится в виде суммы двух определителей
. Тогда по свойству 3. определитель представится в виде суммы двух определителей
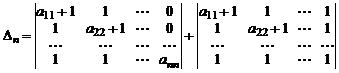 .
.
Первый определитель разложим по последнему столбцу. Второй определитель приведем к треугольному виду, вычитая последний столбец из всех остальных. Тогда
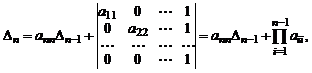 (1)
(1)
где 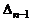 является определителем порядка
является определителем порядка 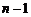 того же типа, что и
того же типа, что и 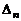 .
.
Решим полученное уравнение для 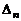 . Из вида
. Из вида 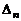 при
при 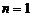 имеем
имеем 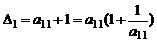 .Выписывая (1) при
.Выписывая (1) при 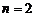 с учетом равенства для
с учетом равенства для 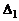 , получаем
, получаем
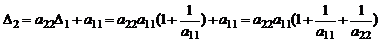 .
.
Методом математической индукции теперь нетрудно показать, что 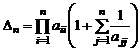 .
.
Пример 6.Вычислить определитель 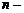 го порядка
го порядка
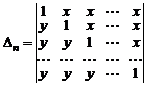 .
.
Представим элементы последнего столбца в виде суммы двух слагаемых: 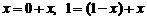 и распишем определитель как сумму двух определителей
и распишем определитель как сумму двух определителей
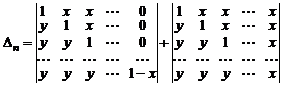 .
.
Первый определитель разложим по последнему столбцу. Для вычисления второго определителя умножим последний столбец на 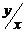 и вычтем из остальных. Получим
и вычтем из остальных. Получим
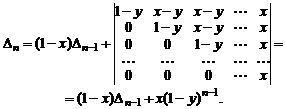
Для решения полученного рекуррентного соотношения воспользуемся тем, что при транспонировании матрицы ее определитель не меняется. В нашем случае транспонировании приводит к замене 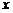 на
на 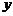 наоборот. Поэтому имеем два равенства
наоборот. Поэтому имеем два равенства
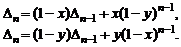
Откуда 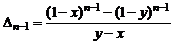 .
.
Пример 7.Следующий пример иллюстрирует применение теоремы Лапласа. Нужно вычислить определитель квазитреугольной матрицы порядка 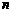 . Квазитреугольной называют блочную матрицу вида
. Квазитреугольной называют блочную матрицу вида 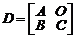 , где
, где 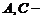 квадратные матрицы,
квадратные матрицы, 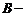 прямоугольная матрица,
прямоугольная матрица, 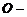 нулевая матрица. В подробной записи матрица имеет вид
нулевая матрица. В подробной записи матрица имеет вид
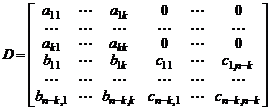 .
.
Пусть 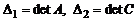 . Покажем, что
. Покажем, что 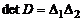 . Воспользуемся теоремой Лапласа. Разложим этот определитель по первым
. Воспользуемся теоремой Лапласа. Разложим этот определитель по первым 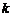 строкам. Очевидно, что из первых
строкам. Очевидно, что из первых 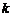 строк можно составить только один минор
строк можно составить только один минор 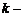 го порядка не содержащий нулевого столбца, у которого номера выделяемых столбцов удовлетворяют условию
го порядка не содержащий нулевого столбца, у которого номера выделяемых столбцов удовлетворяют условию 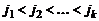 . Этот минор есть
. Этот минор есть 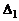 . Дополнительным к нему минором является определитель
. Дополнительным к нему минором является определитель 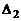 , что и доказывает формулу.
, что и доказывает формулу.
Задачи
1. Определить число инверсий в перестановках:
а) 1,9.6,3.2.4.7.8.
б) 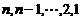 .
.
в) 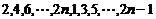 .
.
2. Выбрать значения 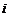 и
и 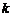 так, чтобы произведение
так, чтобы произведение 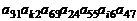 входило в определитель 7-го порядка со знаком плюс.
входило в определитель 7-го порядка со знаком плюс.
3. С каким знаком входит в определитель порядка 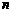 произведение элементов побочной диагонали?
произведение элементов побочной диагонали?
4. Найти члены определителя
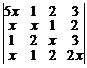 ,
,
содержащие 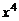 и
и 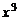 .
.
5. Пользуясь только определением, вычислить определитель
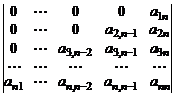 .
.
6. Пользуясь только свойствами определителей вычислить следующие определители:
а) 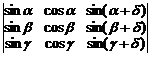 . б)
. б) 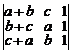 .
.
в) 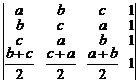 . г)
. г) 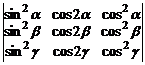 .
.
д) 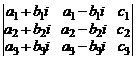 , где
, где 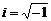 .
.
7. Не вычисляя определителей, доказать следующие тождества:
а) 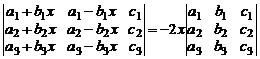 .
.
б) 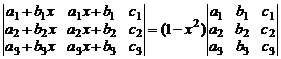 .
.
в) 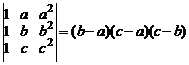 .
.
г) 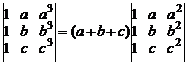 .
.
8. Пользуясь свойствами определителей, включая разложение по строке или столбцу, доказать тождество:
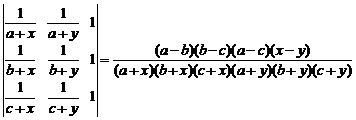 .
.
9. Разлагая по 2-му столбцу, вычислить определитель
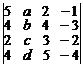 .
.
Вычислить определители:
10.  . 11.
. 11. 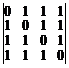 . 12.
. 12. 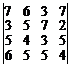 .
.
13. 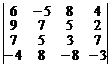 . 14.
. 14. 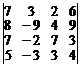 .
.
15. 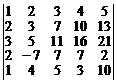 . 16.
. 16. 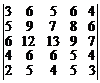 .
.
В следующих задачах, где по виду определителя нельзя установить его порядок, предполагается, что он равен 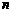 .
.
Вычислить следующие определители, приводя их к треугольному виду.
17. 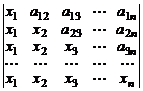 . 18.
. 18. 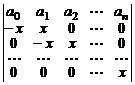 .
.
19. 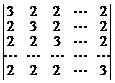 20.
20. 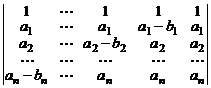 .
.
Вычислить следующие определители методом рекуррентных соотношений.
21. 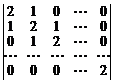 22.
22. 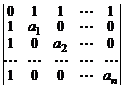 .
.
23. 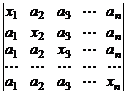 . 24.
. 24. 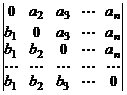 .
.
Пользуясь теоремой Лапласа вычислить следующие определители.
25. 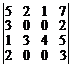 . 26.
. 26. 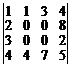 . 27.
. 27. 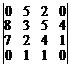 .
.
28. 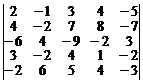 . 29.
. 29. 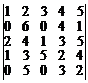 .
.
Вычислить определители:
30. 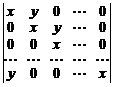 . 31.
. 31. 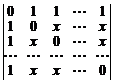 .
.
32.  . 33.
. 33. 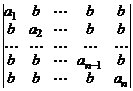 .
.
34. 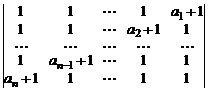 .
.
35. 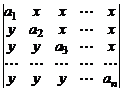 . 36.
. 36. 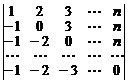 .
.
37. Порядок следующего определителя равен 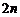 :
:
 .
.
38.  .
.
39. 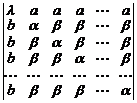 . 40.
. 40. 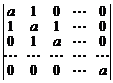 .
.
41.  .
.
42. 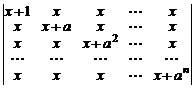 .
.
Обратная матрица
Квадратная матрица 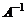 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице 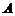 того же порядка, если
того же порядка, если
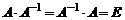 .
.
Необходимым и достаточным условием существования обратной матрицы является невырожденность матрицы 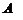 т.е.
т.е.
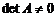 .
.
В этом случае обратная матрица существует, является единственной и определяется соотношением
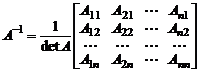 ,
,
где 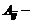 алгебраические дополнения элементов
алгебраические дополнения элементов 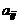 матрицы
матрицы 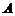 .
.
Обратная матрица обладает следующими свойствами:
1. 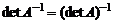 .
.
2. 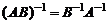 .
.
3. 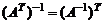 .
.
Полезно помнить, что если матрица 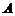 является треугольной, то
является треугольной, то 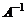 является треугольной того же типа, что и матрица
является треугольной того же типа, что и матрица 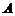 . Обратная к симметричной матрице тоже симметрична.
. Обратная к симметричной матрице тоже симметрична.
Пример. Найти матрицу обратную к матрице
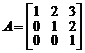 .
.
Определитель 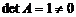 и, следовательно, обратная матрица существует. Алгебраические дополнения элементов матрицы
и, следовательно, обратная матрица существует. Алгебраические дополнения элементов матрицы 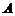 равны
равны
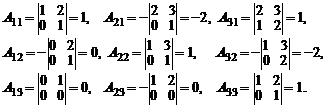
Поэтому
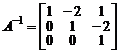 .
.
Задачи
Найти матрицы обратные к данным.
1. 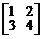 . 2.
. 2. 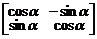 . 3.
. 3. 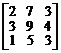 .
.
4. 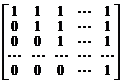 . 5.
. 5. 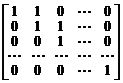 .
.
6.  .
.
7. Решить матричные уравнения:
а) 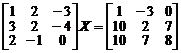 .
.
б) 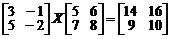 .
.
8. Показать, что вычисление матрицы, обратной к данной матрице порядка 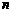 , можно свести к решению
, можно свести к решению 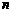 систем линейных уравнений, каждая из которых содержит
систем линейных уравнений, каждая из которых содержит 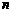 уравнений с
уравнений с 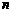 неизвестными и имеет матрицей коэффициентов при неизвестных матрицу
неизвестными и имеет матрицей коэффициентов при неизвестных матрицу 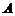 .
.
9. Как изменится обратная матрица 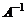 , если в данной матрице
, если в данной матрице 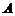 :
:
а) переставить 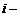 ю и
ю и 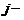 ю строки?
ю строки?
б) 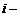 ю строку умножить на число
ю строку умножить на число 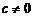 ?
?
в) к 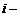 й строке прибавить
й строке прибавить 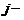 ю, умноженную на число
ю, умноженную на число 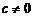 , или совершить аналогичное преобразование столбцов?
, или совершить аналогичное преобразование столбцов?
Ранг матрицы
Основные понятия
Определение 1. Пусть даны 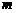 вектор – столбцов порядка
вектор – столбцов порядка 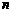
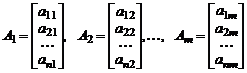
и 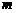 скаляров
скаляров 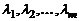 . Умножая
. Умножая 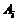 на
на 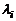 и складывая, получим вектор – столбец
и складывая, получим вектор – столбец 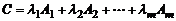 с элементами
с элементами 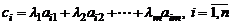 , который называется линейной комбинацией столбцов
, который называется линейной комбинацией столбцов 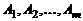 .
.
Определение 2. Столбцы 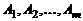 называются линейно зависимыми, если найдутся такие числа
называются линейно зависимыми, если найдутся такие числа 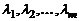 , не равные нулю одновременно, что линейная комбинация
, не равные нулю одновременно, что линейная комбинация
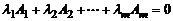 ,
,
где ноль справа это нулевой вектор – столбец.
Определение 3. Столбцы 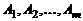 называются линейно независимыми, если равенство
называются линейно независимыми, если равенство
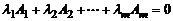
возможно только при условии 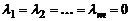 .
.
Необходимым и достаточным условием линейной зависимости вектор – столбцов является равенство одного из них линейной комбинации других.
Пример. Пусть даны вектор – столбцы
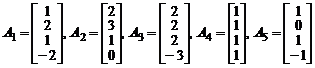 .
.
Нетрудно заметить, что столбец 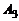 равен сумме
равен сумме 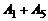 . Поэтому при
. Поэтому при 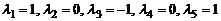 линейная комбинация данных столбцов равна нулю и, следовательно, они линейно зависимы.
линейная комбинация данных столбцов равна нулю и, следовательно, они линейно зависимы.
В общем случае проверка условия линейной зависимости сводится к нахождению ненулевого решения системы уравнений
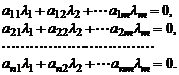
Рассмотрим теперь матрицу 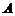 порядка
порядка 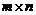 .
.
Определение 4. Натуральное число 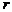 называется рангом матрицы
называется рангом матрицы 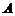 , если у нее имеется минор порядка
, если у нее имеется минор порядка 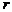 отличный от нуля, а все миноры порядка
отличный от нуля, а все миноры порядка 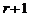 и выше, если это возможно, равны нулю. Очевидно, что
и выше, если это возможно, равны нулю. Очевидно, что 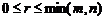 .
.
Определение 5. Если ранг матрицы равен 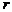 , то всякий отличный от нуля минор порядка
, то всякий отличный от нуля минор порядка 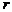 матрицы
матрицы 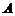 называется базисным минором. Строки и столбцы матрицы
называется базисным минором. Строки и столбцы матрицы 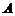 , на пересечении которых расположен базисный минор, называются базисными строками и столбцами.
, на пересечении которых расположен базисный минор, называются базисными строками и столбцами.
Теорема (о базисном миноре). Базисные столбцы (строки) матрицы линейно независимы. Любой столбец (любая строка) матрицы является линейной комбинацией базисных столбцов (строк).
Из последних утверждений следует второе определение ранга матрицы: ранг матрицы равен максимальному числу ее линейно независимых столбцов (строк).
Вычисление ранга матрицы
Вычисление ранга матрицы можно проводить одним из следующих способов.
Первый состоит в сведении данной матрицы с помощью элементарных преобразований к канонической матрице. Каноническая матрица является блочной матрицей, у которой один из блоков представляет собой единичную матрицу, а все остальные блоки – нулевые матрицы.
Каноническую матрицу можно записать в виде
 .
.
Ранг канонической матрицы равен, очевидно, числу единиц, стоящих на диагонали. Преобразования, не меняющие ранга матрицы, называются элементарными. К их числу относятся:
1. Перестановка двух любых столбцов (строк) матрицы.
2. Умножение столбца (строки) на отличное от нуля число.
3. Прибавление к одному столбцу (строке) линейной комбинации других столбцов (строк).
Пример. Вычислить ранг матрицы
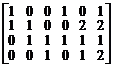 .
.
Вычтем первый столбец из четвертого и шестого, а в получившейся матрице второй столбец приб
