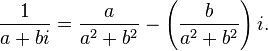Определение комплексного числа. Действия с комплексными числами, записанными в алгебраической форме. Умножение и деление комплексных чисел, записанных в алгебраической форме.
Определение комплексного числа. Действия с комплексными числами, записанными в алгебраической форме. Умножение и деление комплексных чисел, записанных в алгебраической форме.
Ко́мпле́ксные чи́сла — числа вида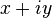 
, где 
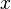и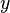 
— вещественные числа, 
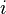— мнимая единица; то есть 
.
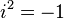Действия над комплексными числами
· Сравнение
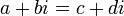означает, что 
и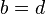 
(два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
· Сложение
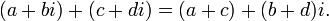
· Вычитание
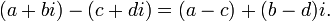
· Умножение
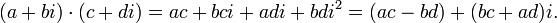
· Деление
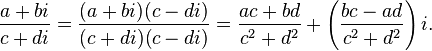
· В частности,
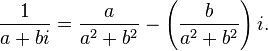
Определение комплексного числа. Действия с комплексными числами, записанными в тригонометрической форме. Умножение и деление комплексных чисел, записанных в тригонометрической форме.
Тригонометрической формой комплексного числа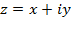 
является
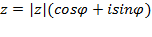, где значение аргумента 
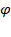, удовлетворяющее условию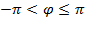 
и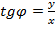 
, 
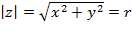–модуль комплексного числа.
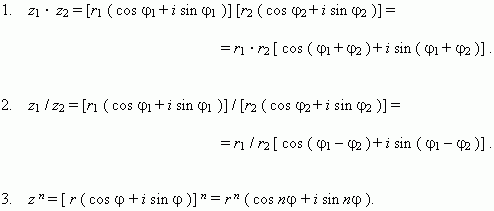
Здесь k - целое. Чтобы получить n различных значений корня n-ой степени из z необходимо задать n последовательных значений для k ( например, k = 0, 1, 2,…, n – 1 ) .
Определение комплексного числа. Действия с комплексными числами, записанными в показательной форме. Умножение и деление комплексных чисел, записанных в показательной форме.
Формула Эйлера (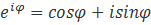 
) позволяет представить комплексное число 
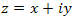в показательной форме: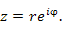 
Такая форма представления позволяет дать наглядную интерпретацию операциям умножения комплексных чисел, их деления и возведения комплексного числа в степень. Например, умножение комплексного числа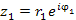 
на комплексное число 
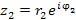сводится к повороту вектора, соответствующего числу 
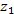, на угол 
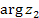и изменению его длины в 
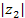раз:
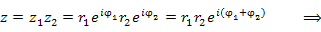
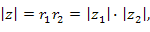
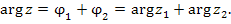Другими словами, чтобы найти произведение комплексных чисел, нужно перемножить их модули и сложить аргументы.
Аналогично интерпретируется частное от деления комплексного числа 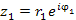на комплексное число :
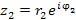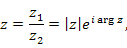где 
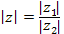и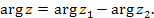 
Для возведения комплексного числа z в целую степень n нужно представить это число в показательной форме, возвести обе части равенства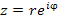 
в степень n и записать результат в тригонометрической форме:
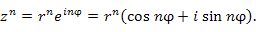
Если число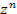 
в левой части этого равенства представить в тригонометрической форме и сократить общий множитель 
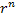, то получится формула Муавра:
.
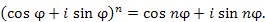Возведение в степень и извлечение корня из комплексного числа.
Формула Муавра для возведения в целую степень комплексного числа:
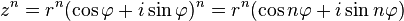
Извлечение корня из комплексного числа:
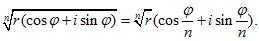
Последовательности комплексных чисел. Критерий Коши.
Определение функции комплексного переменного. Предел и непрерывность функции комплексного переменного.
Необходимые и досттаточные условия для существования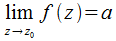 
:
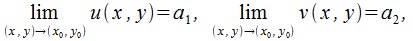
при том, что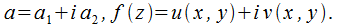 
Непреывнойфункцию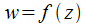 
в т.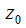 
можно назвать при условии, что:
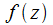определена в т. 
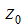и ее окрестности;
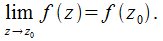
Линейная функция.
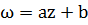
Определение комплексного числа. Действия с комплексными числами, записанными в алгебраической форме. Умножение и деление комплексных чисел, записанных в алгебраической форме.
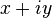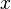Ко́мпле́ксные чи́сла — числа вида , где и 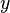— вещественные числа, 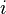— мнимая единица; то есть .
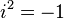Действия над комплексными числами
· Сравнение
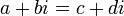означает, что и 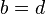(два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
· Сложение
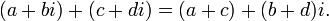
· Вычитание
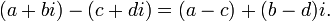
· Умножение
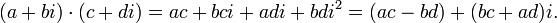
· Деление
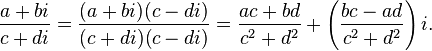
· В частности,