Теорема (основное тригонометрическое тождество).

Для любого угла 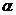справедливо тождество .

Доказательство.

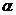Пусть дан некоторый угол . Тогда координаты конца радиуса тригонометрического круга, составляющего угол 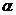с положительным направлением оси 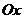, будут равны по определению , (рис.18). Так как квадрат расстояния между любыми двумя точками плоскости, заданными своими координатами, равен сумме квадратов разностей одноимённых координат, то квадрат расстояния от точки до точки (равный единице, поскольку - конец радиуса единичной длины) определяется равенством ,

откуда следует .

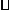
Между основными тригонометрическими функциями произвольного аргумента α имеются следующие соотношения.

1.Основное тригонометрическое тождество

.

Доказательство тождества приведено выше.

2.По определению тангенса и котангенса выполнено

, для , ;

, для , .

3.Перемножая последние два соотношения, получим

для , .

4. Разделив основное тригонометрическое тождество почленно на и и выполнив несложные преобразования, получим соответственно

для , .

Аналогично для , .

23. Тригонометрические функции двойного и половинного аргумента

Формулы сложения позволяют выразить , и через тригонометрические функции угла .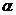

Рассмотрим формулы:

Положим в этих формулах 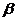равным 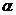. Получим:

Полученные формулы: называют формулами двойного угла.

Замечание. Воспользовавшись основным тригонометрическим тождеством, формулу косинуса двойного угла можно переписать в виде

.

Из формул двойного аргумента легко выводятся формулы половинного аргумента:

,

и

24.

Рассмотрим тригонометрическую окружность. Повернем радиус , равный , около точки на угол 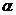и на угол 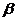. Получим радиусы и .

Найдем скалярное произведение векторов и

Пусть координаты точки равны , координаты точки равны . Эти же координаты имеют соответственно и векторы и .

По определению скалярного произведения векторов:

Выразим скалярное произведение и через тригонометрические функции углов 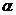и 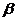. Из определения косинуса и синуса следует, что

Подставив значения в правую часть равенства , получим

С другой стороны, по теореме о скалярном произведении векторов, имеем:

.

Угол BOC между векторами и может быть равен или , либо может отличаться от этих значений на целое число оборотов.

В любом из этих случаев, так как

Поэтому

Из равенств и следует:

,

Поделив обе части равенства на , получаем

С помощью формулы легко получить следующую формулу

Так как

Поделим числитель и знаменатель на , получим

Поделим числитель и знаменатель на , получим

Аналогично для (проведите доказательство самостоятельно)

25. Преобразование суммы (разности) в произведение

Сумму и разность синусов или косинусов можно представить в виде произведения тригонометрических функций.

Чтобы представить в виде произведения сумму , положим и и воспользуемся формулами синуса суммы и синуса разности. Получим:

Решая систему , получаем, что и , таким образом.

Аналогично, можно вывести формулы разности синусов, суммы и разности косинусов.

26. Преобразование произведения в сумму.

Произведение ; ; можно представить в виде суммы тригонометрических функций.

Положим и ,

отсюда, решив систему: , получаем, и

Воспользуемся формулами преобразования суммы в произведение:

27. Обратные тригонометрические функции. (Теорема о корне и теорема об обратной функции)

Теорема о корне:

Пусть функция возрастает (убывает) на промежутке , число 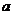– любое из значений, принимаемых функцией на этом промежутке. Тогда уравнение имеет единственный корень в промежутке .

Теорема об обратной функции:

Если функция возрастает (убывает) на промежутке , то она обратима и обратная к ней функция , определённая на множестве значений функции , так же является возрастающей (убывающей).

Арксинус

О. Функция 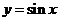возрастает на и принимает все значения от до , значит по теореме о корне в промежутке уравнение имеет единственный корень.

Это число называется арксинусом числа 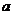и обозначается .

Т.е. арксинусом числа 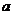называется такое число из промежутка , синус которого равен : .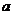

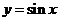Так как функция на промежутке строго возрастает, значит, по теореме об обратной функции, она имеет обратную функцию: , переобозначив переменные, получаем

Рассмотрим свойства этой функции:

1. Область определения функции: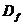

.

2. Множество значений функции: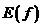

3. Периодичность:

Функция не периодическая, так как она строго возрастает на всей области определения (по теореме об обратной функции)

Чётность/нечётность

Из рисунка 19 видно, что , т.е. функция нечетная