Промежутки монотонности (Интервалы возрастания/убывания функции)
Теорема.
Если 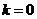 , то функция
, то функция 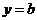 - постоянное число (b=const),
- постоянное число (b=const),
Если 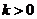 то функция возрастает,
то функция возрастает,
Если 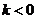 , то функция убывает.
, то функция убывает.
Доказательство:
Возьмем произвольные 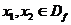 такие, что
такие, что 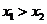 и рассмотрим разность:
и рассмотрим разность: 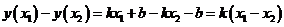
· если 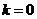 , то
, то 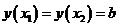 - функция постоянна
- функция постоянна
· если 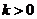 , то
, то 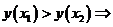 функция возрастает
функция возрастает
· если 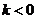 , то
, то 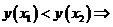 функция убывает
функция убывает
Наибольшее/наименьшее значение функции
Функция 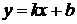 не имеет наименьшего и наибольшего значения, т.к. её множеством значений является всё множество
не имеет наименьшего и наибольшего значения, т.к. её множеством значений является всё множество  .
.
График функции
Графиком линейной функции является прямая (рис 1).
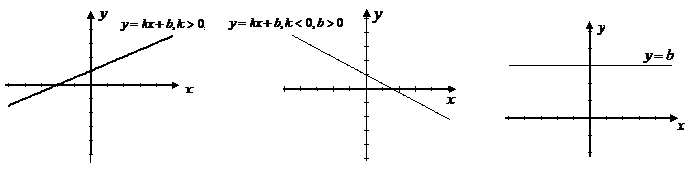
3. Свойства функции 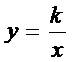 и её график
и её график
О. Функция вида 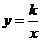 , где
, где 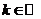 ,
, 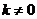 называется обратной пропорциональностью.
называется обратной пропорциональностью.
Свойства:
1. Область определения функции 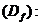
Выражение 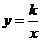 однозначно вычисляется
однозначно вычисляется 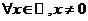 , при
, при 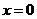 это выражение не определено (почему?), значит
это выражение не определено (почему?), значит 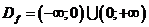
2. Множество значений функции 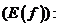
Уравнение 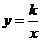 при всех значениях
при всех значениях 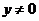 имеет единственный корень, равный
имеет единственный корень, равный 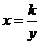
Если 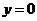 , то уравнение корней не имеет, значит
, то уравнение корней не имеет, значит 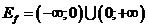
Периодичность.
Теорема.
Функция 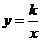 не является периодической.
не является периодической.
Доказательство:
Пусть функция 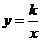 является периодической с периодом
является периодической с периодом 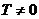 . Это значит, что
. Это значит, что 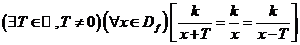 .
.
Рассмотрим разность:
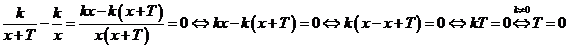 ,
, 
значит предположение о том, что функция обратная пропорциональность имеет период 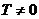 не верно, и функция обратная пропорциональность не является периодической.
не верно, и функция обратная пропорциональность не является периодической.
Чётность/нечётность.
Функция 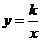 нечётная, т.к. область определения является симметричной относительно нуля и
нечётная, т.к. область определения является симметричной относительно нуля и 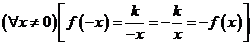
Точки пересечения графика с осями координат.
Т.к. уравнение 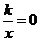 не имеет корней, то график функции
не имеет корней, то график функции 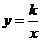 не имеет точек пересечения с осью абсцисс.
не имеет точек пересечения с осью абсцисс.
Так как 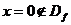 , то график функции точек пересечения с осью ординат не имеет.
, то график функции точек пересечения с осью ординат не имеет.
Промежутки знакопостоянства функции.
· При 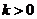 :
: 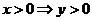 и
и 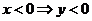
· При 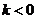 :
: 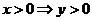 и
и 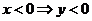
Интервалы возрастания/убывания функции.
Теорема.
Если 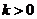 то функция убывает при
то функция убывает при 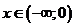 и при
и при 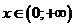
Если 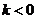 , то функция возрастает при
, то функция возрастает при 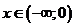 и при
и при 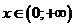
Доказательство:
Пусть 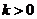 , тогда возьмем произвольные
, тогда возьмем произвольные 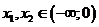 , пусть для определенности
, пусть для определенности 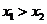 , тогда
, тогда 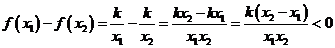 , то есть
, то есть 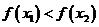 , значит функция убывает при
, значит функция убывает при 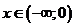 .
.
Теперь возьмем произвольные 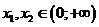 , и так же для определенности пусть
, и так же для определенности пусть 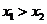 ,
,
тогда рассмотрим разность 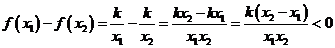 (почему?),
(почему?),
то есть 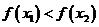 , значит функция убывает при
, значит функция убывает при 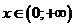 .
.
Аналогично при 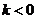 : возьмем произвольные
: возьмем произвольные 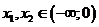 , пусть для определенности
, пусть для определенности 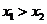 , тогда
, тогда 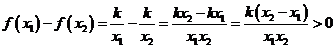 , то есть
, то есть 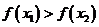 , значит функция возрастает при
, значит функция возрастает при 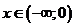 .
.
Теперь возьмем произвольные 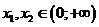 , и так же для определенности пусть
, и так же для определенности пусть 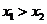 , тогда
, тогда 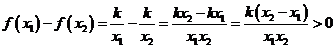 ,то есть
,то есть 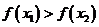 , значит функция возрастает при
, значит функция возрастает при  .
.
Замечание: Функция 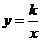 не является монотонной на всей своей области определения !!!!!!!
не является монотонной на всей своей области определения !!!!!!!
Действительно, например, 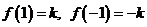 , если
, если 
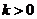 , то
, то 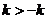 ,что не верно, т.к. при
,что не верно, т.к. при 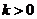 функция является убывающей и по определению большему значению аргумента соответствует меньшее значение функции.
функция является убывающей и по определению большему значению аргумента соответствует меньшее значение функции.
Наибольшее/наименьшее значение функции.
Функция не имеет наибольшего и наименьшего значения, т.к. её 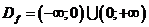
График функции.
График функции имеет две асимптоты – вертикальную 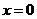 и горизонтальную
и горизонтальную 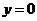 .
.
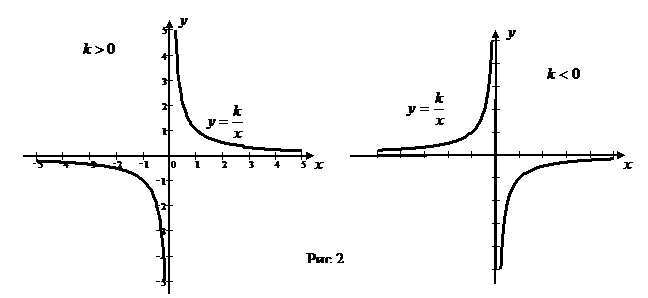 О. График функции называется гиперболой и расположен в первой и третьей координатных четвертях, если
О. График функции называется гиперболой и расположен в первой и третьей координатных четвертях, если 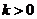 ; и во второй и четвертой, если
; и во второй и четвертой, если 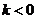 . (рис.2).
. (рис.2).
4. Свойства функции 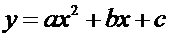 и её график. Взаимное расположение графика квадратичной функции и оси абсцисс.
и её график. Взаимное расположение графика квадратичной функции и оси абсцисс.
О. Функция, задаваемая формулой 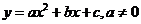 называется квадратичной функцией.
называется квадратичной функцией.
Свойства:
1. Область определения функции: 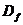 .
.
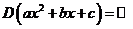 , т.к. значение квадратного трехчлена однозначно определено для любого действительного числа (почему?).
, т.к. значение квадратного трехчлена однозначно определено для любого действительного числа (почему?).
2. Множество значений функции: 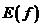
Преобразуем квадратный трехчлен, задающий квадратичную функцию, выделив полный квадрат:
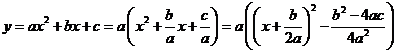
Введем обозначения: 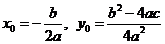 тогда
тогда 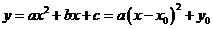 .
.
Выражение 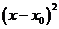 может принимать любыенеотрицательные значения в зависимости от x. Поэтому, при
может принимать любыенеотрицательные значения в зависимости от x. Поэтому, при 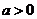
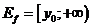 , а при
, а при 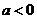
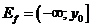
3. Периодичность:
Квадратичная функция не может быть периодической, т. к., например, свое значение 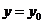 она
она
принимает только в одной точке 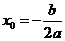 .
.
Чётность/нечётность
Если 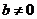 , то функция является функцией общего вида (не является ни четной, ни нечетной), т.к.
, то функция является функцией общего вида (не является ни четной, ни нечетной), т.к. 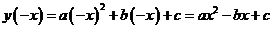 , то есть
, то есть 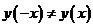 и
и 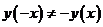
Если 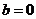 , то функция имеет вид
, то функция имеет вид 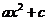 и
и 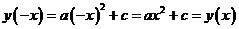 , значитфункция четная.
, значитфункция четная.
