Признаки возрастания и убывания функции
Следующая теорема выражает важный для практических целей признак строгого возрастания и строгого убывания функции и указывает правило для определения интервалов, на которых функция возрастает и убывает (интервалов монотонности функции).
| Теорема. | (достаточный признак возрастания и убывания функции на интервале) Если во всех точках некоторого интервала первая производная 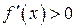 , то функция , то функция 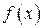 на этом интервале возрастает. Если же во всех точках некоторого интервала первая производная на этом интервале возрастает. Если же во всех точках некоторого интервала первая производная 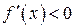 , то функция на этом интервале убывает. , то функция на этом интервале убывает. |
Правило. Для определения интервалов строгого возрастания и строгого убывания функции следует решить неравенства:
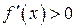 и
и 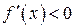 .
.
Пример. Найти интервалы монотонности функции
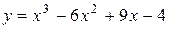 .
.
Решение. Областью определения данной функции является вся ось  . Находим производную
. Находим производную 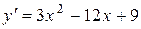 . Чтобы найти интервалы возрастания функции, решим неравенство
. Чтобы найти интервалы возрастания функции, решим неравенство 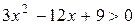 или
или 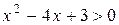 ; чтобы найти интервалы убывания функции, решим неравенство
; чтобы найти интервалы убывания функции, решим неравенство 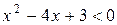 . Корни квадратного трёхчлена
. Корни квадратного трёхчлена 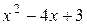 равны 1 и 3, поэтому распределение знаков квадратного трехчлена имеет вид
равны 1 и 3, поэтому распределение знаков квадратного трехчлена имеет вид
+ – +
 |
1 3 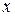
Следовательно, на интервалах 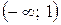 и
и 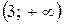 функция возрастает, а на интервале
функция возрастает, а на интервале 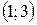 функция убывает.
функция убывает.
Экстремум функции
Если для всех значений 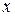 из некоторой окрестности точки
из некоторой окрестности точки 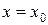 выполняется неравенство
выполняется неравенство 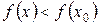 , то
, то 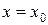 называют точкой локального максимума функции
называют точкой локального максимума функции 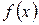 , а
, а 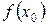 – локальным максимумом функции. Если для всех значений
– локальным максимумом функции. Если для всех значений 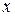 из некоторой окрестности точки
из некоторой окрестности точки 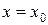 выполняется неравенство
выполняется неравенство 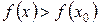 , то
, то 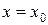 называют точкой локального минимума функции
называют точкой локального минимума функции 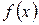 , а
, а 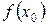 – локальным минимумом функции. Минимумы и максимумы функции называют ее экстремумами.
– локальным минимумом функции. Минимумы и максимумы функции называют ее экстремумами.
Необходимый и достаточный признаки экстремума функции дают следующие две теоремы
| ТЕОРЕМА 1 | (необходимый признак экстремума) Если точка 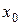 является точкой экстремума, то в этой точке производная является точкой экстремума, то в этой точке производная 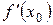 равна нулю или не существует. равна нулю или не существует. |
Эта теорема имеет простую геометрическую интерпретацию.
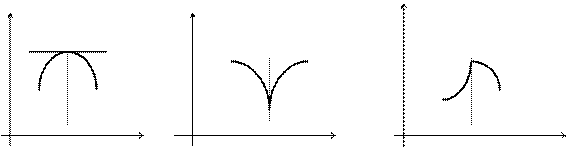
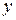
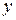
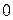

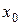
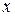
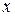
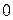
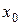
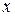
Рис. 4 Рис. 5 Рис. 6
На рис. 4 касательная к графику функции 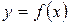 в точке
в точке 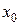 – точка экстремума – параллельна оси
– точка экстремума – параллельна оси 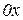 , т.е. угловой коэффициент (а это и есть производная) равен нулю.
, т.е. угловой коэффициент (а это и есть производная) равен нулю.
На рис. 5 касательная в точке экстремума перпендикулярна оси 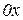 , на рис. 6 касательная в точке с абсциссой
, на рис. 6 касательная в точке с абсциссой 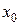 не существует. В обоих случаях производная в точке не существует.
не существует. В обоих случаях производная в точке не существует.
Точки, в которых первая производная равна нулю, а также, в которых она не существует, но функция сохраняет непрерывность, называются критическими.
Следует уяснить, что указанный признак экстремума является только необходимым, но отнюдь не достаточным: производная функции может быть равна нулю или не существовать не только в тех точках, в которых функция достигает экстремума. Например, производная функции 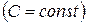 равна нулю в любой точке, но экстремума у этой функции нет (рис. 7). Поэтому, определив критические точки, в которых функция может достигать экстремума, надо каждую из точек в отдельности исследовать на основании достаточных условий существования экстремума.
равна нулю в любой точке, но экстремума у этой функции нет (рис. 7). Поэтому, определив критические точки, в которых функция может достигать экстремума, надо каждую из точек в отдельности исследовать на основании достаточных условий существования экстремума.

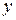
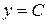
0 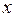
Рис. 7
| ТЕОРЕМА 2 | (достаточный признак экстремума) Если при переходе через критическую точку производная меняет знак, то критическая точка является точкой экстремума. Это точка максимума, если производная меняет знак с плюса на минус, и точка минимума, если производная меняет знак с минуса на плюс. |
Пример. Исследовать на экстремум функцию 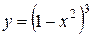 .
.
Решение.
1. Область определения 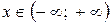 .
.
2. Находим критические точки, для чего найдем производную 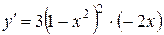 и приравняем ее к нулю
и приравняем ее к нулю 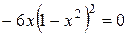 . Отсюда
. Отсюда 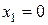 ,
, 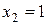 ,
, 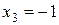 . Точек, где
. Точек, где 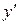 не существует, нет.
не существует, нет.
3. Исследуем критические точки по достаточному признаку экстремума. Это удобно делать в таблице, куда заносятся критические точки и точки разрыва функции (в данном примере точек разрыва нет).
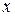 | 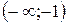 | 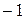 | 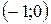 | 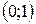 | 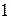 | 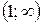 | |
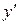 | 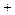 | 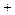 | - | - | |||
 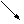   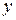 | нет экстремума | 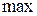 | нет экстремума |
Для нахождения знака производной достаточно подставить в нее любое значение из рассматриваемого интервала. Так, исследуя интервал 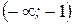 , можно взять, например, точку
, можно взять, например, точку 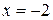 и подставить это значение в производную:
и подставить это значение в производную: 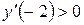 . Исследовав, указанным образом знаки производной в интервалах
. Исследовав, указанным образом знаки производной в интервалах 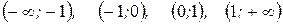 , замечаем, что производная меняет знак при переходе через точку 0 (с “+” на “-”). Значит,
, замечаем, что производная меняет знак при переходе через точку 0 (с “+” на “-”). Значит, 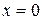 – точка максимума. Значение функции в этой точке
– точка максимума. Значение функции в этой точке 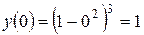 .
.
Точки перегиба
График функции 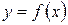 называется выпуклым на интервале
называется выпуклым на интервале 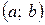 , если он расположен ниже касательной, проведенной к графику функции в любой точке этого интервала (рис. 8 а).
, если он расположен ниже касательной, проведенной к графику функции в любой точке этого интервала (рис. 8 а).
График функции 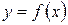 называется вогнутым на интервале
называется вогнутым на интервале 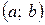 , если он расположен выше касательной, проведенной к графику функции в любой точке этого интервала (рис. 8 б).
, если он расположен выше касательной, проведенной к графику функции в любой точке этого интервала (рис. 8 б).
 | |||
 | |||
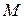
Рис. 8 а Рис. 8 б
| ТЕОРЕМА | (достаточный признак выпуклости (вогнутости) графика функции) Если 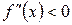 на интервале на интервале 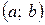 , то график функции является выпуклым на этом интервале; если же , то график функции является выпуклым на этом интервале; если же 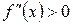 , то на интервале , то на интервале 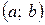 график функции – вогнутый. график функции – вогнутый. |
Точка кривой, отделяющая ее выпуклую дугу от вогнутой, называется точкой перегиба.
Точки кривой, в которых вторая производная 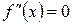 или не существует, называются критическими точками второго рода. Точки перегиба следует искать среди критических точек второго рода.
или не существует, называются критическими точками второго рода. Точки перегиба следует искать среди критических точек второго рода.
В критической точке второго рода 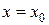 перегиб будет только в том случае, когда при переходе через эту точку
перегиб будет только в том случае, когда при переходе через эту точку 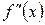 меняет знак.
меняет знак.
Правило. Для определения точек перегиба кривой надо определить все критические точки второго рода и рассмотреть знаки 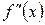 в каждых двух соседних интервалах, на которые эти точки делят область определения функции. В случае, если знаки
в каждых двух соседних интервалах, на которые эти точки делят область определения функции. В случае, если знаки 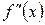 в двух соседних интервалах различны, критическая точка второго рода является точкой перегиба. Если же в двух соседних интервалах
в двух соседних интервалах различны, критическая точка второго рода является точкой перегиба. Если же в двух соседних интервалах 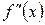 имеет один и тот же знак, то в рассматриваемой критической точке второго рода перегиба нет. В точке перегиба кривая пересекает касательную.
имеет один и тот же знак, то в рассматриваемой критической точке второго рода перегиба нет. В точке перегиба кривая пересекает касательную.
Пример. Определить интервалы выпуклости и вогнутости, точки перегиба графика функции 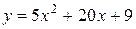 .
.
Решение. Область определения функции – интервал 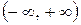 .
.
Найдем первую и вторую производные функции
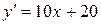 ,
,
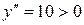 .
.
Так как 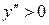 при любом значении
при любом значении 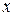 , то кривая вогнута на всем интервале
, то кривая вогнута на всем интервале 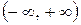 . Точек перегиба нет.
. Точек перегиба нет.
Пример. Определить интервалы выпуклости и вогнутости и точки перегиба графика функции 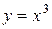 .
.
Решение. Область определения функции – интервал 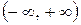 .
.
Найдем первую и вторую производные функции
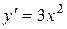 ,
, 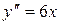 .
.
Решаем уравнение 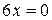 и находим, что
и находим, что 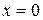 . Это единственная критическая точка. Она делит область определения функции на два интервала
. Это единственная критическая точка. Она делит область определения функции на два интервала 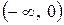 и
и 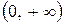 .
.
 |
– +
На интервале 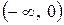 кривая выпукла
кривая выпукла 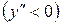 , а на интервале
, а на интервале 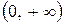 – вогнута
– вогнута 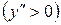 . Таким образом, при переходе через точку
. Таким образом, при переходе через точку 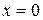 вторая производная меняет знак. Эта точка является точкой перегиба. Ее координаты
вторая производная меняет знак. Эта точка является точкой перегиба. Ее координаты 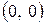 .
.
Асимптоты
| Определение. | Если расстояние от кривой 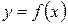 , имеющей бесконечную ветвь, до некоторой определенной прямой по мере удаления точки по этой кривой от начала координат в бесконечность, стремится к нулю, то прямая называется асимптотой данной кривой. , имеющей бесконечную ветвь, до некоторой определенной прямой по мере удаления точки по этой кривой от начала координат в бесконечность, стремится к нулю, то прямая называется асимптотой данной кривой. |
Различают асимптоты: вертикальные и наклонные.
1. Кривая 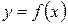 имеет вертикальную асимптоту
имеет вертикальную асимптоту 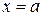 , если при
, если при 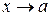 ,
, 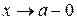 или при
или при 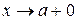
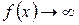 . Для определения вертикальных асимптот надо отыскать те значения аргумента, вблизи которых
. Для определения вертикальных асимптот надо отыскать те значения аргумента, вблизи которых 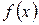 неограниченно возрастает по абсолютной величине. Если такими значениями аргумента являются
неограниченно возрастает по абсолютной величине. Если такими значениями аргумента являются 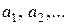 , то уравнения вертикальных асимптот будут
, то уравнения вертикальных асимптот будут
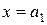 ;
; 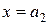 ; …
; …
Вертикальные асимптоты – это нули знаменателя функции. Например, 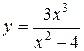 . Здесь две вертикальные асимптоты:
. Здесь две вертикальные асимптоты: 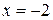 ,
, 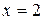
2. Для определения наклонной асимптоты 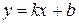 кривой
кривой 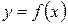 надо найти числа
надо найти числа 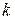 и
и 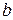 по формулам
по формулам
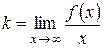 ,
, 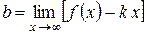
(иногда следует отдельно рассматривать случаи 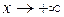 и
и 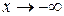 ).
).
