Касательное и нормальное ускорения точки.
При естественном способе задания движения вектор ускорения определяют по его проекции на оси 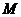 tnb, имеющие начало в точке
tnb, имеющие начало в точке 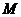 и движущиеся вместе с нею. Эти оси, называем осями естественного трехгранника, направлены следующим образом: ось
и движущиеся вместе с нею. Эти оси, называем осями естественного трехгранника, направлены следующим образом: ось 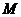 t - вдоль касательной к траектории в сторону положительного отсчета расстояния s;
t - вдоль касательной к траектории в сторону положительного отсчета расстояния s; 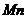 ось по нормали, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории; ось
ось по нормали, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории; ось 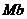 - перпендикулярно к первым двум так, чтобы она образовала с ними правую тройку. Нормаль
- перпендикулярно к первым двум так, чтобы она образовала с ними правую тройку. Нормаль 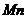 , лежащая в соприкасающейся плоскости (в плоскости самой кривой, если кривая плоская), называется главной нормалью, а перпендикулярная к ней нормаль
, лежащая в соприкасающейся плоскости (в плоскости самой кривой, если кривая плоская), называется главной нормалью, а перпендикулярная к ней нормаль 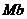 - бинормалью.
- бинормалью.
Проекции ускорения на оси 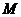 t и Мn
t и Мn
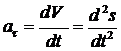 ,
, 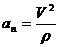 ,
,
где r - радиус кривизны траектории.
Проекция ускорения точки на касательную равна первой производной от численной величины скорости или второй производной от расстояния (криволинейной координаты) 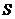 по времени, а проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинормаль равна нулю(
по времени, а проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинормаль равна нулю( 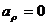 ).
).
Если заданы проекции скорости 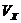 и
и 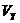 , а так же проекции ускорения
, а так же проекции ускорения 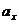 и
и 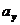 в данный момент времени, то величину касательного ускорения точки можно определить по формуле:
в данный момент времени, то величину касательного ускорения точки можно определить по формуле:
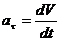 =
= 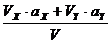 .
.
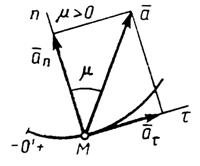 Вектор ускорения точки
Вектор ускорения точки 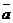 изображается диагональю параллелограмма, построенного на составляющих
изображается диагональю параллелограмма, построенного на составляющих 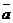 t и
t и 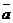 n (
n ( 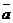 =
= 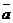 t+
t+ 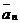 n).Так как эти составляющие взаимно перпендикулярны, то модуль вектора а и угол его отклонения от нормали
n).Так как эти составляющие взаимно перпендикулярны, то модуль вектора а и угол его отклонения от нормали 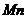 определяется формулами:
определяется формулами:
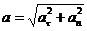 =
= 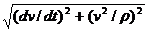 ,
, 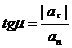 .
.
43 кинемотика твердого тела .виды движения твердых тел.поступательное движения твердого тела. во многих случаях деформации твердых тел столь незначительны, что ими можно пренебречь при исследовании движения и равновесия твердых тел и рассматривать эти тела как недеформируемые (или абсолютно твердые)Абсолютно твердым телом называют такое твердое тело, расстояние между двумя любыми точками которого остается неизменным. Теоретическая механика изучает движение и равновесие только абсолютно твердых тел, и для краткости их называют просто твердыми телами .Задачи кинематики твердого тела разделяются на 2 части:1. Задачи движения и изучения кинематических характеристик движения всего тела в целом.2. Изучение движения каждой из точек тела в отдельности.Твердое тело может совершать пять видов движения: поступательное, вращение вокруг неподвижной оси, плоскопараллельное, вращение вокруг неподвижной точки и свободное.Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли (рисунок 1.1) и т.д.
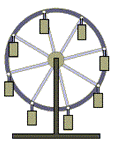 Рис. 1.1
Рис. 1.1
Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.Доказательство. Если выбрать две точки твердого тела А и В (рисунок 1.2), то радиусы-векторы этих точек связаны соотношением
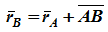
Траектория точки А – это кривая, которая задается функцией rA(t), а траектория точкиB – это кривая, которая задается функцией rB(t). Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы.Продифференцируем по времени выражение
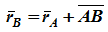
Получаем
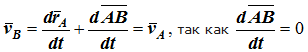
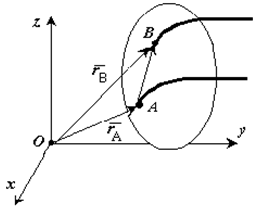 Рис. 1.2
Рис. 1.2
Продифференцируем по времени скорость и получим выражение aB = aA. Следовательно, скорости и ускорения всех точек твердого тела одинаковы.
Для задания поступательного движения твердого тела достаточно задать движение одной из его точек:

44 Вращательное движение ТВЕРДОГО ТЕЛА угловая скорость угловое ускорения Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки,называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П0 и П , одна из которых неподвижна, а другая жестко связана с телом. φ=φ(t) – уравнение вращательного движения твердого тела.
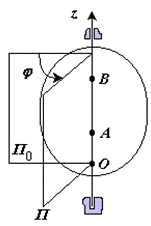 Рис. 1.3 За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:
Рис. 1.3 За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:
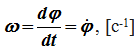 В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим
В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим
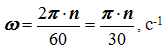 Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости
Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости
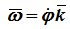 где k – единичный вектор оси вращения.
где k – единичный вектор оси вращения.
Угловое ускорение – мера изменения угловой скорости:
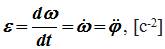 Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)
Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)
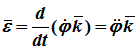
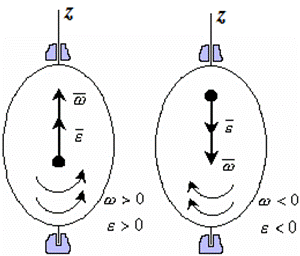
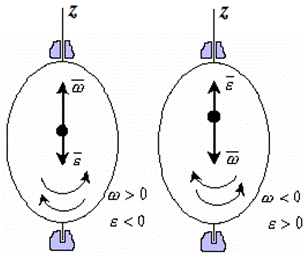 Рис. 1.4
Рис. 1.4
Если ε >0 и ω >0 (рисунок 1.4), то угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов ω и ε совпадают, оба они направлены в положительную сторону оси вращения Oz.При ε <0 и ω <0 – тело вращается ускоренно в отрицательную сторону. Направление векторов ω и ε совпадают, оба они направлены в отрицательную сторону оси вращения Oz .Если ε <0 и ω >0, то имеем замедленное вращение в положительную сторону. Векторыω и ε направлены в противоположные стороны.Если ε >0 при ω <0, то имеем замедленное вращение в отрицательную сторону. Векторыω и ε направлены в противоположные стороны.
Если угловая скорость ω=const, то вращательное движение называется равномерным.Уравнение равномерного вращения
φ=φ0+ωt
Если угловое ускорение ε=const, то вращательное движение называется равнопеременным.
Уравнение равнопеременного вращения
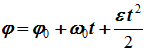 и уравнение, выражающее угловую скорость в любой момент времени
и уравнение, выражающее угловую скорость в любой момент времени
ω=ω0+εt
представляют совокупность основных формул вращательного равнопеременного движения тела.
45.Равномерное и равнопеременное вращение.Если угловая скорость тела остается во все время движения постоянной ( 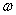 =const), то вращение тела называетсяравномерным. Найдем закон равномерного вращения. Из формулы
=const), то вращение тела называетсяравномерным. Найдем закон равномерного вращения. Из формулы 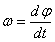 имеем
имеем 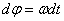 .Отсюда, считая, что в начальный момент времени t=0 угол
.Отсюда, считая, что в начальный момент времени t=0 угол 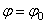 , и беря интегралы слева от
, и беря интегралы слева от 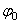 до
до  , а справа от 0 до t, получим окончательно
, а справа от 0 до t, получим окончательно
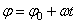 .Из равенства следует, что при равномерном вращении, когда
.Из равенства следует, что при равномерном вращении, когда 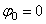
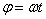 и
и 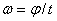 .В технике скорость равномерного вращения часто определяют числом оборотов в минуту, обозначая эту величину через n об/мин. Найдем зависимость между n об/мин и
.В технике скорость равномерного вращения часто определяют числом оборотов в минуту, обозначая эту величину через n об/мин. Найдем зависимость между n об/мин и 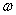 1/с. При одном обороте тело повернется на угол
1/с. При одном обороте тело повернется на угол 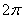 , а при n оборотах на
, а при n оборотах на 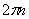 ; этот поворот делается за время t = 1 мин = 60 сек. Из равенства следует тогда, что
; этот поворот делается за время t = 1 мин = 60 сек. Из равенства следует тогда, что
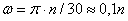 .Если угловое ускорение тела во все время движения остается постоянным
.Если угловое ускорение тела во все время движения остается постоянным 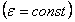 , то вращение называется равнопеременным. Найдем закон равнопеременного вращения, считая, что в начальный момент времениt=0 угол
, то вращение называется равнопеременным. Найдем закон равнопеременного вращения, считая, что в начальный момент времениt=0 угол 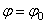 , а угловая скорость
, а угловая скорость 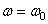 (
( 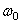 - начальная угловая скорость).Из формулы
- начальная угловая скорость).Из формулы 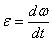 имеем
имеем 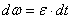 . Интегрируя левую часть в пределах от
. Интегрируя левую часть в пределах от 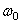 до
до 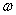 , а правую - в пределах от 0 до t, найдем
, а правую - в пределах от 0 до t, найдем 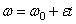 ,
,
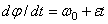 или
или 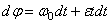 .Вторично интегрируя, найдем отсюда закон равнопеременного вращения
.Вторично интегрируя, найдем отсюда закон равнопеременного вращения
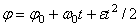 .Если величины
.Если величины 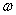 и
и 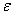 имеют одинаковые знаки, то вращение будет равноускоренным, а если разные - равнозамедленным.
имеют одинаковые знаки, то вращение будет равноускоренным, а если разные - равнозамедленным.
