Касательное и нормальное ускорения точки
В § 39 было установлено, что ускорение а точки лежит в соприкасающейся плоскости, т. е. в плоскости  Следовательно, проекция вектора а на бинормаль
Следовательно, проекция вектора а на бинормаль  равна нулю
равна нулю  Найдем проекции а на две другие оси. Проектируя обе части равенства (10) на оси
Найдем проекции а на две другие оси. Проектируя обе части равенства (10) на оси  и обозначая символами
и обозначая символами  проекции вектора
проекции вектора  на эти оси, получим:
на эти оси, получим:
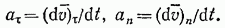
Вектор  представляет собой разность между скоростями в двух соседних точках
представляет собой разность между скоростями в двух соседних точках  (рис. 123, а), т. е.
(рис. 123, а), т. е.  .
.
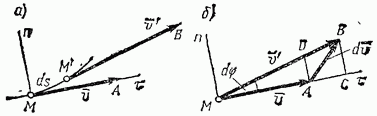
Рис. 123
Отложим векторы  от общего начала (рис. 123, б); тогда
от общего начала (рис. 123, б); тогда  а фигуру ACBD при бесконечно малом угле
а фигуру ACBD при бесконечно малом угле  можно рассматривать как прямоугольник. Отсюда
можно рассматривать как прямоугольник. Отсюда  где
где  — элементарное приращение числового значения скорости. Далее, поскольку предел отношения дуги к хорде равен единице, можно AD рассматривать как элементарную дугу радиуса МА, размер которой определяется произведением радиуса на центральный угол. Тогда
— элементарное приращение числового значения скорости. Далее, поскольку предел отношения дуги к хорде равен единице, можно AD рассматривать как элементарную дугу радиуса МА, размер которой определяется произведением радиуса на центральный угол. Тогда  Подставляя найденные значения
Подставляя найденные значения  в равенства (18), получим:
в равенства (18), получим:
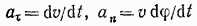
Угол между касательными к кривой в двух ее точках называется углом смежности; тогда  — элементарный угол смежности. Напомним, что отношение
— элементарный угол смежности. Напомним, что отношение  определяет кривизну кривой в точке М, а кривизна k является величиной, обратной радиусу кривизны
определяет кривизну кривой в точке М, а кривизна k является величиной, обратной радиусу кривизны  в этой точке, т. е.
в этой точке, т. е.
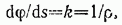
Введем эту величину во второе из равенств (19) и преобразуем его, учтя еще равенство (17), к виду
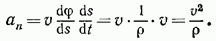
В результате окончательно получим:
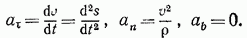
Таким образом, мы доказали, что проекция ускорения точки на касательную равна первой производной от числового значения скорости или второй производной от расстояния (криволинейной координаты) s по времени, а проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинормаль равна нулю. Это одна из важных теорем кинематики. Величины  называют касательным и нормальным ускорениями точки.
называют касательным и нормальным ускорениями точки.
При движении точки М в одной плоскости касательная  поворачивается вокруг бинормали
поворачивается вокруг бинормали  с угловой скоростью
с угловой скоростью  Тогда второе из равенств (19) дает еще одну, часто используемую в инженерной практике формулу для вычисления
Тогда второе из равенств (19) дает еще одну, часто используемую в инженерной практике формулу для вычисления 
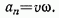
Из нее следует, что нормальное ускорение равно произведению скорости точки на угловую скорость поворота касательной к траектории.
Отложим вдоль касательной  и главной нормали
и главной нормали  векторы
векторы  т. е. касательную и нормальную составляющие ускорения (рис. 124). При этом составляющая
т. е. касательную и нормальную составляющие ускорения (рис. 124). При этом составляющая  будет всегда направлена в сторону вогнутости кривой, так как всегда
будет всегда направлена в сторону вогнутости кривой, так как всегда  а составляющая
а составляющая  может быть направлена или в положительном, или в отрицательном направлении оси
может быть направлена или в положительном, или в отрицательном направлении оси  в зависимости от знака проекции
в зависимости от знака проекции  (см. рис. 124, а, б).
(см. рис. 124, а, б).
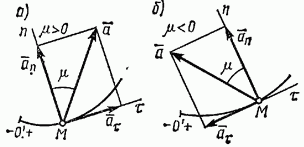
Рис. 124
Вектор ускорения точки а изображается диагональю параллелограмма, построенного на составляющих 
Так как эти составляющие взаимно перпендикулярны, то модуль вектора а и угол  , его отклонения от нормали
, его отклонения от нормали  определятся формулами:
определятся формулами:
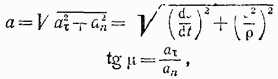
где —  при
при  вектор а отклонен от нормали
вектор а отклонен от нормали  в сторону
в сторону  (рис. 124, а), а при
(рис. 124, а), а при  — в противоположную сторону (рис. 124, б).
— в противоположную сторону (рис. 124, б).
Таким образом, если движение точки зсдако естественным спосо-Сом, то, зная траекторию (а следовательно, и ее радиус кривизны  в любой точке) и закон движения, т. е. зависимость
в любой точке) и закон движения, т. е. зависимость  можно по формулам (17) и (21), (22) определить модуль и направление векторов скорости и ускорения точки в любой момент времени.
можно по формулам (17) и (21), (22) определить модуль и направление векторов скорости и ускорения точки в любой момент времени.
ОПОРЫ И ОПОРНЫЕ РЕАКЦИИ
Рассмотренный в § 2.7 свободный брус был нагружен заданными нагрузками (силами и моментами), находящимися в равновесии (см. рис. 3.7). Обычно заданные нагрузки не бывают взаимно уравновешенными; неподвижность конструкции под действием этих нагрузок обеспечивается благодаря наличию опор, соединяющих ее с основанием. В опорах возникают реакции, которые вместе с заданными нагрузками представляют уравновешенную систему внешних сил, действующих на конструкцию.
Как известно из курса теоретической механики, любое тело обладает в плоскости тремя степенями свободы. Поэтому для обеспечения геометрической неизменяемости системы (бруса) необходимо наложить на нее (в плоскости) три связи.
Рассмотрим различные типы опор плоских систем.
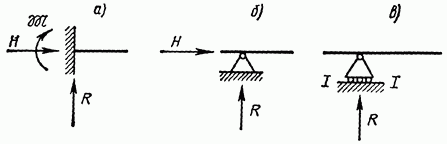
Рис. 4.7
1. Защемление, или заделка (рис. 4.7, а). Защемленный (или заделанный) конец бруса не может ни смещаться поступательно, ни поворачиваться. Следовательно, число степеней свободы бруса с защемленным концом равно нулю. В опоре могут возникать: вертикальная реакция (сила R — рис. 4.7, а), препятствующая вертикальному смещению конца бруса; горизонтальная реакция (сила Н), исключающая возможность его горизонтального смещения  и реактивный момент препятствующий повороту. Таким образом, закрепление бруса с помощью заделки накладывает на него три связи и обеспечивает его неподвижность.
и реактивный момент препятствующий повороту. Таким образом, закрепление бруса с помощью заделки накладывает на него три связи и обеспечивает его неподвижность.
2. Шарнирно неподвижная опора (рис. 4.7, б). Поперечное сечение бруса, проходящее через шарнирно неподвижную опору, не может смещаться поступательно. В опоре возникает реактивная сила, проходящая через центр шарнира. Ее составляющими являются вертикальная сила R, препятствующая вертикальному смещению, и горизонтальная сила Н, исключающая горизонтальное смещение закрепленного сечения бруса. Опора не препятствует повороту бруса относительно центра шарнира, и, следовательно, брус, закрепленный при помощи одной такой опоры, имеет одну степень свободы. Закрепление бруса с помощью шарнирно неподвижной опоры, накладывает на него две связи.
3. Шарнирно подвижная опора (рис. 4.7, в). Поперечное сечение бруса, проходящее через шарнирно подвижную опору, может смещаться параллельно опорной плоскости  и поворачиваться, но оно не может смещаться перпендикулярно к опорной плоскости. В опоре возникает только одна реакция в виде силы R, перпендикулярной к опорной плоскости. Закрепление бруса с помощью такой опоры накладывает на него одну связь.
и поворачиваться, но оно не может смещаться перпендикулярно к опорной плоскости. В опоре возникает только одна реакция в виде силы R, перпендикулярной к опорной плоскости. Закрепление бруса с помощью такой опоры накладывает на него одну связь.
Рассмотренные типы опор принято также изображать с помощью стерженьков.
Шарнирно подвижную опору изображают в виде стерженька, имеющего по концам шарниры (рис. 5.7, а). Нижний шарнир неподвижен, а верхний может смещаться лишь по прямой линии, перпендикулярной к оси стерженька.
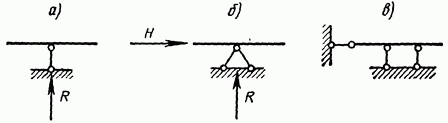
Рис. 5.7
Это соответствует тем условиям закрепления, которые обеспечивает шарнирно подвижная опора (см. рис. 4.7, в). Опорная реакция действует только вдоль оси стерженька. Собственные деформации его при расчетах не учитываются, т. е. стерженек считается бесконечно жестким.
Шарнирно неподвижную опору изображают с помощью двух стерженьков с шарнирами по концам (рис. 5.7, б). Верхний шарнир является общим для обоих стерженьков. Направления стерженьков могут быть произвольными. Они, однако, не должны быть расположены на одной прямой.
Заделку (защемление) можно изображать с помощью трех стерженьков с шарнирами по концам, как показано на рис. 5.7, в.
Число стерженьков в схематическом изображении опоры равно числу составляющих опорной реакции и числу связей, накладываемых этой опорой на конструкцию.
Для того чтобы брус не перемещался под нагрузкой, он должен быть геометрически неизменяемо (неподвижно) соединен с основанием, что в случае плоского действия сил, как уже отмечалось, достигается путем наложения на него трех внешних связей.

Рис. 6.7
Это можно сделать с помощью одной заделки (рис. 6.7, а) или одной шарнирно неподвижной и одной шарнирно подвижной опоры (рис. 6.7, б), или с помощью трех шарнирно подвижных опор, направления реакций которых не пересекаются в одной точке (рис. 6.7, в).
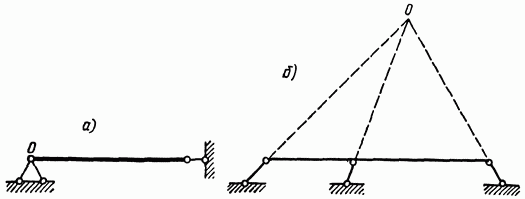
Рис. 7.7
Если направления трех опорных стерженьков пересекаются в одной точке О (рис. 7.7, а,б), то система является мгновенно изменяемой, так как в этом случае ни один опорный стерженек не препятствует весьма малому повороту бруса вокруг точки О; такое расположение опорных стерженьков недопустимо.
Рассмотрим геометрически неизменяемые системы, состоящие из нескольких брусьев.
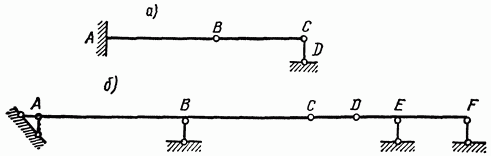
Рис. 8.7
На рис. 8.7, а, например, показана система из двух брусьев (АВ и ВС), на каждый из которых наложено три связи. На брус ВС одну связь накладывает опорный стерженек CD, препятствующий вертикальному смещению точки С бруса, и две связи — шарнир В, препятствующий вертикальному и горизонтальному смещению точки В бруса.
На брус АВ все три связи налагает заделка А; шарнир же В не может препятствовать ни поступательным смещениям, ни поворотам бруса АВ и, следовательно, не налагает на него связей.
На рис. 8.7, б показана геометрически неизменяемая система, состоящая из трех брусьев (АС, CD и DF). На каждый из них наложено три связи. Так, например, шарнир С налагает на брус CD две связи (так как препятствует горизонтальному и вертикальному смещениям точки С), а шарнир  - одну связь (так как препятствует только вертикальному смещению точки
- одну связь (так как препятствует только вертикальному смещению точки  ).
).
Системы, изображенные на рис. 8.7, называются многопролетными шарнирными балками.
Общее число неизвестных опорных реакций при вариантах закрепления бруса, показанных на рис. 6.7, а, б, в, равно трем. Следовательно, эти реакции можно найти при помощи трех уравнений равновесия, которые составляются для плоской системы сил. По значениям же опорных реакций и внешних нагрузок можно определить [по формулам (2.7) — (4.7)] внутренние усилия в любом поперечном сечении бруса. Поэтому брус, закрепленный путем наложения на него трех связей, является не только геометрически неизменяемым, но и статически определимым. Наложение на него большего числа связей делает брус статически неопределимым, так как в этом случае все опорные реакции нельзя определить из одних лишь уравнений равновесия.
Уравнения равновесия, составляемые для определения опорных реакций, можно представить в трех различных вариантах:
1) в виде сумм проекций сил на две произвольные не параллельные друг другу оси и суммы моментов сил относительно любой точки плоскости  МО);
МО);
2) в виде суммы проекций сил на произвольную ось и двух сумм моментов относительно любых точек плоскости, не лежащих на одном перпендикуляре к указанной оси проекций 
3) в виде трех сумм моментов относительно любых точек плоскости, не лежащих на одной прямой 
Выбор того или иного варианта составления уравнений равновесия, а также выбор точек и направлений осей, используемых при составлении этих уравнений, производится в каждом конкретном случае с таким расчетом, чтобы по возможности не проводить совместное решение уравнений. Для проверки правильности определения опорных реакций полученные их значения рекомендуется подставить в какое-либо уравнение равновесия, не использованное ранее.
На многопролетную шарнирную балку, изображенную на рис. 8.7, а, наложено четыре внешние связи (три в сечении А и одна в сечении С), а на балку, изображенную на рис. 8.7, б, - пять внешних связей (две в сечении А и по одной в сечениях В, Е и F).
Однако если на каждый брус, составляющий многопролетную шарнирную балку, наложено по три связи, то эта балка статически определима и опорные реакции можно найти из уравнений статики.
Кроме трех уравнений равновесия всех сил, действующих на многопролетную шарнирную балку, составляются уравнения, выражающие равенство нулю моментов сил, приложенных по одну сторону от каждого шарнира (соединяющего отдельные части балки), относительно центра этого шарнира. Например, для балки, изображенной на рис. 8.7, а, кроме трех уравнений равновесия всех действующих на нее сил, составляется уравнение моментов левых (или правых) сил относительно шарнира  , а для балки, изображенной на рис. 8.7,б, - относительно шарниров С и D.
, а для балки, изображенной на рис. 8.7,б, - относительно шарниров С и D.
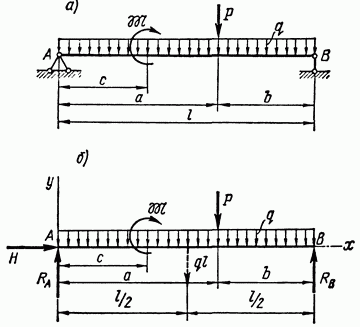
Рис. 9.7
Рассмотрим пример определения опорных реакций простой однопролетной балки, расчетная схема которой изображена на рис. 9.7, а. Отбросим опоры и заменим их влияние на балку опорными реакциями RA, Н и RB (рис. 9.7, б). Обычно балка с отброшенными опорами отдельно не изображается, а обозначения и направления опорных реакций указываются на расчетной схеме балки. Реакции  представляют собой вертикальную и горизонтальную составляющие полной реакции шарнирно неподвижной опоры А; сила же
представляют собой вертикальную и горизонтальную составляющие полной реакции шарнирно неподвижной опоры А; сила же  является полной реакцией опоры В. Направления опорных реакций выбираются произвольно; если в результате расчета значение какой-либо реакции получается отрицательным, то, значит, в действительности ее направление противоположно предварительно принятому.
является полной реакцией опоры В. Направления опорных реакций выбираются произвольно; если в результате расчета значение какой-либо реакции получается отрицательным, то, значит, в действительности ее направление противоположно предварительно принятому.
Найдем сначала опорную реакцию Н, составив для этого сумму проекций всех сил на горизонтальную ось х:
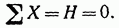
Очевидно, что не только в рассматриваемом случае, а всегда при действии на горизонтальную балку только вертикальной нагрузки горизонтальная опорная реакция равна нулю.
Для определения опорной реакции RA составим сумму моментов всех сил относительно точки В. Опорные реакции Н и RB проходят через эту точку, а потому их моменты относительно нее равны нулю:
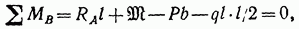
где  равнодействующая равномерной нагрузки интенсивностью
равнодействующая равномерной нагрузки интенсивностью  распределенной по всей длине балки
распределенной по всей длине балки  - плечо этой равнодействующей относительно точки В.
- плечо этой равнодействующей относительно точки В.
Следовательно,
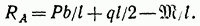
Аналогично составим сумму моментов всех сил относительно точки А:
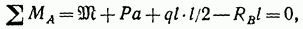
откуда
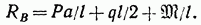
Для проверки найденных значений опорных реакций составим сумму проекций всех сил на ось у.
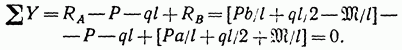
Составленное уравнение удовлетворяется, что указывает на правильность определения опорных реакций.
Экзаменационный билет № 24
