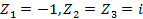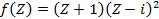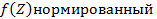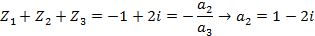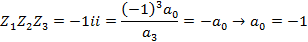Многочлены над полем комплексных чисел

В предыдущих темах мы изучили многочлены с коэффициентами из произвольного абстрактного поля P. Большое значение имеет рассмотрение многочленов над числовыми полями. Остановимся на С. Среди всех числовых полей поле С состоит в том, что всякий многочлен f(x) степени большей или либо равной 2 является приводимым над полем С то есть разлагается на произведение линейных многочленов по этому его называют замкнутым. Задача разложения над С в произведение линейных членов решается на основании:

Т1(Основная теорема алгебры):

Всякий многочлен положительной степени с числовыми коэффициентами из поля С имеет корень в поле комплексных чисел С.

(Доказана Гауссом в 1799 г. )

Т2: Любой многочлен 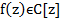степени не меньше 2 является приводимым над полем С.

Доказательство:

По Т1 существует 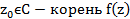,тогда по теореме Безу: 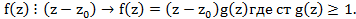Следовательно даны многочлен раскладывается.

■

Следствие: Чтобы многочлен из С был не приводим над С необходимо и достаточно, что бы степень его была равной 1.

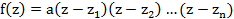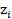Т3: Многочлен n степени из кольца C[z] раскладывается в произведение линейных множителей, то есть представляется в виде: , где корни.

Доказательство:

На основании теоремы о разложении многочленов в произведение не приводимых множителей запишем, что 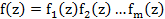где 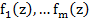не приадимы над C а, каждый не приводимый над С является многочленом 1 степени. Где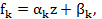

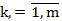
ng w:val="EN-US"/></w:rPr><m:t>k</m:t></m:r></m:sub></m:sSub></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000" wsp:rsidRPr="00770B1F"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">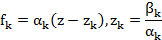

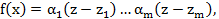
Обозначим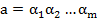

таким образом мы доказали что наше разложение существует, причем .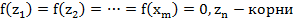

■

Т4: Многочлен n степени в поле С имеет ровно n корней с учетом их кратности.

Пример 1:

Разложить в произведение линейных множителей:

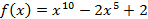
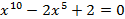
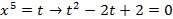
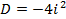
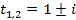
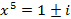
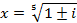
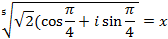
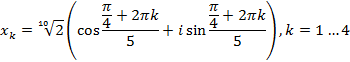
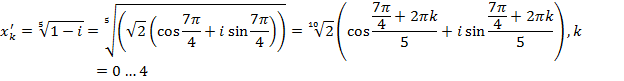
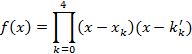
Зависимость между корнями. Теорема Виета.

Т: Если числа 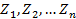являются корнями многочлена 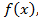n степени

То справедливы следующие формулы называемые формулами Виета:

…

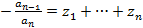
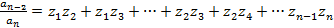
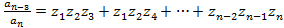
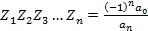
Доказательство:

По условию числа 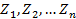являются корнями многочлена 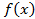n степени из кольца С[Z] этот многочлен можно представить в виде произведения линейных множителей: 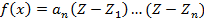. Раскроим скобки в правой части (рассмотрим эту процедуру для многочлена 3 степени)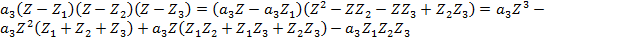

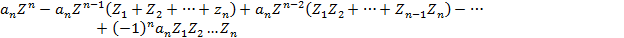
На основании определения равенства 2 многочленов приравниваем коэффициенты при одинаковых степенях:

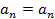
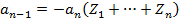
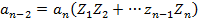
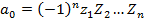
Из последних равенств следует формулы Виета.

■

Замечание: Рассмотренные формулы Виета обобщают известные из школьного курса математики формулы Виета

Пример 1:

Составить нормированный многочлен наименьшей степени имеющий простой корень -1 и двукратный корень i.