Теорема о единственности решения задачи Дирихле

(Это тоже следствие принципа максимума).

Теорема. Если две функции, гармонические внутри замкнутой ограниченной связной области V и непрерывные на её границе, равны друг другу всюду на границе области V, то они равны друг другу и всюду внутри V.

Иными словами, гармоническая внутри области V функция однозначно определяется своими значениями на границе области.

Доказательство. Пусть q₁(M) и q₂(M) – две гармонические функции, принимающие одинаковые значения на границе области V, обозначим через q(M) разность этих функций:

q(M)=q₁(M)– q₂(M).

Тогда q(M) – гармоническая внутри V функция, равная нулю всюду на границе области V. Докажем, что она равна нулю также всюду внутри V. Допустим, что внутри V найдутся точки, в которых функция отлична от нуля, например положительна. Тогда и наибольшее значение функции должно быть положительным. Но на границе функция q=0. Значит наибольшее значение достигается во внутренней точке области V. А это невозможно, т.к. q(M) – гармоническая функция.

Аналогичное противоречие мы получили бы, если бы внутри области оказалась бы точка, где функция отрицательна.

Итак, во всех точках области V функция q(M) должна равняться нулю: q(M)º0, откуда q₁(M) - q₂(M)º0 т.е. q₁(M) º q₂(M), что и требовалось доказать.

Теорема о непрерывной зависимости решения задачи Дирихле для уравнения Лапласа от входных данных

(Это тоже следствие принципа максимума).

Напомним, что задача называется физически определённой, если малому изменению условий, определяющих решение задачи, в данном случае граничных условий, соответствует малое изменение самого решения.

Теорема. Пусть u₁ и u₂ – непрерывные в V+S гармонические внутри V функции, для которых |u₁–u₂|£e на S. Тогда это же неравенство выполняется внутри V.

Это утверждение непосредственно вытекает из следствия 2 теоремы о наибольшем и наименьшем значениях, где доказывалось, что если |u|£U|_S, то это неравенство выполняется всюду в V+S. Действительно, обозначим 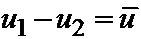. По условию теоремы |u₁–u₂|£e на S, это значит, что 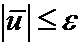на S, но e – это гармоническая функция. Возьмём три функции –e, 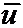и e. Имеем на границе 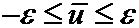. Значит 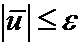. Что и требовалось доказать.

Задачи

1. Решить задачу Коши , , .

Решение. Это неоднородное уравнение. Его решение является суммой двух решений - общего решения однородного уравнения и частного решения неоднородного уравнения. Решение однородного уравнения – это решение, получающееся по формуле Даламбера

Частным решением неоднородного уравнения в данной задаче является функция

.

Ответ.

2. Решить методом Фурье

Решение. Это первая краевая задача для уравнения колебаний струны с ненулевыми граничными условиями. Собственные числа и собственные функции первой краевой задачи для уравнения колебаний струны нам известны. (Кому неизвестны пожалуйста, повторите).

Но здесь неоднородные граничные условия

Делаем замену переменных: , где должна удовлетворять условиям: ; Тогда . Получили , тогда граничные условия для функции будут: ; то есть они становятся однородными (нулевыми).

Начальные условия для функции :

Уравнение для функции у нас остаётся однородным: .

Решение этого уравнения при нулевых граничных условиях имеет вид:

,

где и - это коэффициенты Фурье начальных данных.

Ввиду ортогональности системы синусов, этот интеграл не равен нулю только при

= интегрируем по частям:

Отсюда

Ответ:

3. Решить методом Фурье

Решение. Это неоднородное уравнение. Решения неоднородных уравнений ищутся в виде суммы двух функций , где - решение однородной задачи для уравнения со всеми поставленными в задаче начальными и граничными условиями, а - решение неоднородной задачи для уравнения с нулевыми начальными и граничными условиями.

Очевидно, что в этом случае функция будет представлять искомое решение неоднородного уравнения. В нашем случае функция будет равна нулю, ввиду нулевых начальных и граничных условий. Но нам для решения неоднородной задачи потребуются собственные числа и собственные функции однородной задачи. В нашем случае однородная задача является первой краевой задачей, её собственные числа и собственные функции нам известны: , . Решение неоднородной задачи ищется в виде ряда по собственным функциям однородной задачи: , где необходимо будет найти, а для этого неоднородность также необходимо разложить в ряд Фурье по собственным функциям однородной задачи. Видно, что выбранная в таком виде функция удовлетворяет нулевым граничным условиям за счёт присутствующего в ней сомножителя , а для получения нулевых начальных условий, надо потребовать, чтобы и .

Итак, разложим функцию в ряд Фурье по собственной системе функций . Найдём коэффициенты Фурье :

Итак, для отыскания функций имеем уравнение:

.

Решение этого обыкновенного неоднородного дифференциального уравнения ищется в виде суммы частного решения и общего решения однородного уравнения: При нашей правой части частное решение ищется в виде Подставляем в уравнение получаем: Отсюда

Значит

Подставляя начальные данные найдём коэффициенты и :

Отсюда

Итак, функции - найдены.

Поскольку , получаем ответ.

Ответ.