Выражение тройного интеграла через цилиндрические координаты

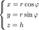Аналогично в некоторых случаях тройной интеграл проще считать не в прямоугольных, а в цилиндрических координатах. Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:

Модуль якобиана отображения равен 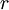. Таким образом получаем, что

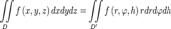
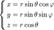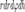Здесь является элементом объема в цилиндрических координатах. Выражение тройного интеграла через сферические координаты Объем в сферических координатах Кроме цилиндрических можно также переходить и в сферические координаты. Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:

Модуль якобиана отображения равен 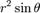. Таким образом получаем, что

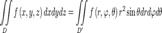
Здесь 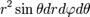является элементом объема в цилиндрических координатах.

26 Экстремум функции двух переменных. Необходимые и достаточные условия экстремума Необходимый признак экстремума: Если в точке 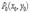дифференцируемая функция 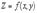имеет экстремум, то ее частные производные в этой точке равны нулю:

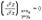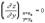, .Доказательство: Допустим, что функция 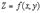имеет в точке 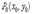экстремум. Согласно определению экстремума функция 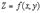при постоянном 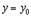,как функция одного достигает экстремума при 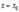. Как известно, необходимым условием для этого является обращение в нуль производной от функци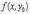и при 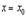,т. е.

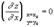.Аналогично функция 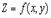при постоянном 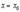,как функция одного , достигает экстремума при 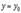.Значит, 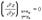Что и требовалось доказать.Точка 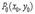,координаты которой обращают в нуль обе частные производные функции 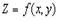,называется стационарной точкой функции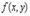. Уравнение касательной плоскости к поверхности 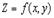: 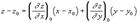для стационарной точки 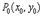принимает вид 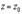.Следовательно, необходимое условие достижения дифференцируемой функцией 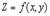экстремума в точке 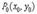геометрически выражается в том, что касательная плоскость к поверхности - графику функции в соответствующей ее точке параллельна плоскости независимых переменных.Для отыскания стационарных точек функции 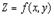нужно приравнять нулю обе ее частные производные 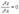, 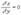. (*) и решить полученную систему двух уравнений с двумя неизвестными. Достаточные условия экстремума для функции нескольких переменных носят значительно более сложный характер, чем для функции одной переменной. Мы рассмотрим эти условия без доказательства только для функции двух переменных.Пусть точка 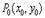является стационарной точкой функции 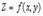, т. е. 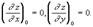Вычислим в точкезначение вторых частных производных функции 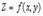и обозначим их для краткости буквами A, B и C: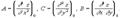Если 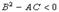,то функция 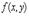имеет в точке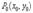экстремум: при A<0 и C<0 и минимум при A>0 и C>0 (Из условия 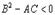следует, что A и C обязательно имеют одинаковые знаки).Если 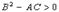,то точка 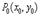не является точкой экстремума.Если 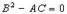,то неясно, является ли точка 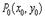точкой экстремума и требуется дополнительное исследование.