Собственный шум цифровой цепи. Объяснить происхождение этого шума т описать аналитически для звена 1-ого порядка
Собственный шум цифровой системы — это выходной шум квантования, обусловленный округлением результатов операций умножения. При анализе собственных шумов необходимо знать: - точки системы, в которых выполняется операция квантования; - оценки (математическое ожидание, дисперсию, абсолютную границу) шумовых сигналов, генерируемых соответствующими источниками; - структуру системы (путь, который проходит каждый шумовой сигнал от своего источника шума до выхода системы); - архитектуру и параметры цифрового устройства.
Источниками шума квантования сигналов в цифровой системе являются умножители.
Умножение значений с by числовыми разрядами последовательности x(n) на коэффициент а дает произведение ax(n), содержащее точные значения с 2 by числовыми разрядами. Однако вычисленное произведение должно быть представлено последовательностью значений с by числовыми разрядами (без учета знакового разряда). При формировании данного результата появляется ошибка квантования, вызванная сокращением числа разрядов (переходом от 2 by к by числовым разрядам).
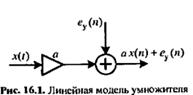
Рассмотрим аналитически собст-ый шум для звена 1-ого порядка.
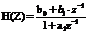
Как видно из рисунка шумовые сигналы eу(n) с математическим ожиданием 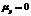 и дисперсией
и дисперсией 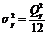 описывают эффекты квантования на выходах умножителей. Используя свойство линейности системы три источника шума можно заменить одним эквивалентным с дисперсией
описывают эффекты квантования на выходах умножителей. Используя свойство линейности системы три источника шума можно заменить одним эквивалентным с дисперсией 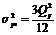 . Оценка дисперсии собственного шума фильтра определяется как
. Оценка дисперсии собственного шума фильтра определяется как
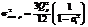
где 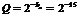 - шаг квантования, определяемый весом младшего числового разряда элементов памяти;
- шаг квантования, определяемый весом младшего числового разряда элементов памяти; 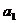 - коэффициент знаменателя заданной передаточной функции.
- коэффициент знаменателя заданной передаточной функции.
Дать характеристику Гарвардской архитектуры и сравнить ее с архитектурой Фон Неймана
Гарвардская архитектура позволяет поднять быстродействие и гибкость использования. В классическом варианте она предполагает хранение программ и данных в разных запоминающих устройствах, что позволяет совмещать во времени выборку и исполнение команд. Модифицированная гарвардская архитектура допускает обмен между памятью программ и памятью данных, что расширяет возможности процессора, при этом отпадает необходимость в отдельном постоянном запоминающем устройстве (ПЗУ) для хранения коэффициентов. Наличие шины данных (ШД) и шины команд (ШК) увеличивает общую производительность.
Персональные ЭВМ и традиционные микропроцессоры имеют неймановскую архитектуру, при которой происходит пошаговое, потактно-последовательное выполнение команд, при этом данные и команды передаются по одной шине.
Примеры гарвардской и неймановской архитектур представлены на рисунках 1 и 2.
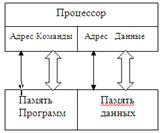
Рис.1 Гарворд-ая архитектура
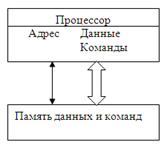
Рис.2 Архитектура Фон Неймана
