Определение (последовательность Коши).
Последовательность 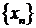 называется фундаментальной или последовательностью Коши, или последовательностью, сходящейся в себе,если
называется фундаментальной или последовательностью Коши, или последовательностью, сходящейся в себе,если 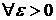
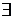 N:
N: 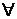 n>N,
n>N, 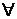 p-натурального следует, что
p-натурального следует, что 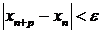
(или 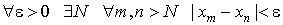 )
)
Теорема (Критерий Коши).Числовая последовательность сходится тогда и только тогда, когда она является фундаментальной.
Пример . Используя критерий Коши можно доказать, что последовательность (-1)n не имеет предела . Очевидно, что 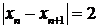 , поэтому если выбрать
, поэтому если выбрать 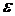 = 1, то получим отрицание утверждения, что последовательность фундаментальна. А именно:
= 1, то получим отрицание утверждения, что последовательность фундаментальна. А именно:
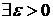 (
( 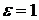 ),
), 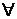 n>N,
n>N, 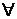 m>N (
m>N ( 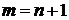 ) ,
) , 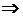 |xn-xm|
|xn-xm| 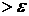 .
.
| Критерий Коши |
Определение. Говорят, что последовательность { 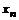 } удовлетворяет условию } удовлетворяет условию  Коши, если для любого числа Коши, если для любого числа 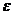 >0 существует такой номер N, зависящий от >0 существует такой номер N, зависящий от 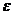 , что для всех номеров m и n таких, что n≥N, m≥N, справедливо неравенство , что для всех номеров m и n таких, что n≥N, m≥N, справедливо неравенство 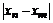 < < 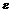 (*). Последовательность, удовлетворяющая условию Коши, называется фундаментальной. Условие (*) можно сформулировать иначе: для любого числа (*). Последовательность, удовлетворяющая условию Коши, называется фундаментальной. Условие (*) можно сформулировать иначе: для любого числа 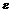 >0 существует такой номер N, зависящий от >0 существует такой номер N, зависящий от 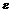 , что для всех номеров n , что для всех номеров n 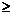 N и всех натуральных p выполняется условие: N и всех натуральных p выполняется условие: 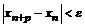 . Теорема (критерий Коши).Для того чтобы последовательность сходилась, необходимо и достаточно, чтобы она удовлетворяла условию Коши. Доказательство. Необходимость. Пусть последовательность { . Теорема (критерий Коши).Для того чтобы последовательность сходилась, необходимо и достаточно, чтобы она удовлетворяла условию Коши. Доказательство. Необходимость. Пусть последовательность { 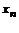 } сходится и } сходится и 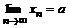 . Зададим . Зададим 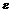 >0, тогда существует такой номер N, что для всех номеров n >0, тогда существует такой номер N, что для всех номеров n 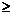 N выполняется неравенство N выполняется неравенство 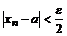 . Пусть n . Пусть n 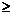 N и m N и m 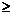 N, тогда N, тогда 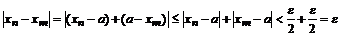 , то есть выполняется условие Коши. Достаточность. Пусть { , то есть выполняется условие Коши. Достаточность. Пусть {  } удовлетворяет условию Коши, то есть для любого } удовлетворяет условию Коши, то есть для любого  >0 существует номер N, что для n >0 существует номер N, что для n  N и m N и m 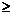 N выполняется неравенство N выполняется неравенство 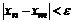 . Пусть . Пусть 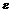 =1, тогда существует номер N =1, тогда существует номер N 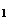 такой, что при n такой, что при n 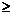 N N 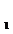 и m и m 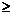 N N 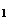 выполняется выполняется 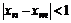 . В частности, если n . В частности, если n 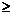 N N 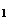 и m=N и m=N 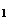 , то , то 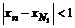 , то есть , то есть 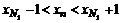 при n при n 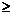 N N 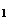 . Это значит, что последовательность {x . Это значит, что последовательность {x  }, n=N }, n=N 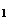 , N , N 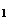 +1,…ограничена. Поэтому в силу теоремы Больцано-Вейерштрасса существует ее сходящаяся подпоследовательность { +1,…ограничена. Поэтому в силу теоремы Больцано-Вейерштрасса существует ее сходящаяся подпоследовательность { 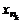 }. Пусть }. Пусть 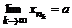 . Зададим . Зададим 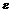 >0. Тогда существует такой номер K >0. Тогда существует такой номер K 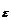 ,что для всех номеров K ,что для всех номеров K 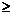 K K 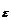 или, что то же самое, для всех n или, что то же самое, для всех n 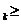 n n 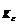 выполняется неравенство выполняется неравенство 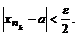 Обозначим через Обозначим через 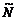 =max{N,n =max{N,n 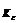 } и зафиксируем некоторое n } и зафиксируем некоторое n 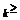 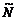 . Тогда для всех n . Тогда для всех n 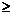 N имеем N имеем 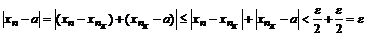 , что и означает, что , что и означает, что 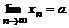 |
Пример. Рассмотрим последовательность 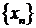 : xn = 1+1/2+1/3+....+1/n
: xn = 1+1/2+1/3+....+1/n
Для исследования на сходимость воспользуемся определением фундаментальности Так как |xn+p - xn| = 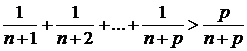 , то при p=n |xn+p - xn|>
, то при p=n |xn+p - xn|> 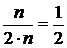 . Очевидно, что определение фундаментальной последовательности не выполняется. В силу критерия Коши эта последовательность не имеет предела. 3.8 Монотонные последовательности
. Очевидно, что определение фундаментальной последовательности не выполняется. В силу критерия Коши эта последовательность не имеет предела. 3.8 Монотонные последовательности
Определение.
1. Последовательность 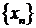 возрастает, если
возрастает, если 

xn<  : каждый член последовательности меньше последующего;
: каждый член последовательности меньше последующего;
2. Последовательность 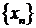 убывает, если
убывает, если 

(  ) : каждый член последовательности больше последующего ;
) : каждый член последовательности больше последующего ;
3. Последовательность 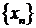 не возрастает, если
не возрастает, если 

 : каждый член последовательности не меньше последующего;
: каждый член последовательности не меньше последующего;
4. Последовательность 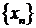 не убывает, если
не убывает, если 

(  ): каждый член последовательности не больше последующего;
): каждый член последовательности не больше последующего;
5. Последовательность 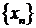 называется монотонной, если она является или возрастающей, или убывающей, или не возрастающей, или не убывающей.
называется монотонной, если она является или возрастающей, или убывающей, или не возрастающей, или не убывающей.
6. У возрастающей ограниченной сверху последовательности есть предел. То же верно для убывающей ограниченной снизу последовательности.
7. Предел последовательности, все члены которой равны числу  , равен
, равен  .
.
8. Теорема 13.Если монотонная последовательность  ограничена, то она сходится.
ограничена, то она сходится.
Доказательство. Так как последовательность  ограничена, то множество ее элементов имеет точные верхнюю
ограничена, то множество ее элементов имеет точные верхнюю  и нижнюю
и нижнюю  грани. Пусть
грани. Пусть  – неубывающая последовательность и
– неубывающая последовательность и  – точная верхняя грань множества ее элементов. Это означает, что для любого числа
– точная верхняя грань множества ее элементов. Это означает, что для любого числа  можно указать такой элемент
можно указать такой элемент  , что
, что  и
и  . Эти два неравенства равносильны неравенству
. Эти два неравенства равносильны неравенству  или
или  . Так как
. Так как  – неубывающая последовательность, то при
– неубывающая последовательность, то при  выполняется
выполняется  или
или  . Это означает, что при
. Это означает, что при  выполняется
выполняется  или
или  . Таким образом,
. Таким образом,  . Аналогично доказывается случай, когда
. Аналогично доказывается случай, когда  – невозрастающая последовательность.
– невозрастающая последовательность.
Замечание 1. Условие ограниченности монотонной последовательности представляет собой необходимое и достаточное условие ее сходимости. Действительно, по теореме 8 сходящаяся монотонная последовательность ограничена.
Замечание 2. Сходящаяся последовательность может и не быть монотонной. Например, последовательность  сходится к числу ноль, но не является монотонной.
сходится к числу ноль, но не является монотонной.
Замечание 3. Если последовательность  неубывающая сходящаяся и
неубывающая сходящаяся и  - ее предел, то для всех номеров n выполняется неравенство
- ее предел, то для всех номеров n выполняется неравенство  . Аналогично, если
. Аналогично, если  невозрастающая сходящаяся последовательность и
невозрастающая сходящаяся последовательность и  – ее предел, то для всех номеров n справедливо
– ее предел, то для всех номеров n справедливо  .
.
Теорема 13 (теорема Больцано-Вейерштрасса).Из всякой ограниченной последовательности действительных чисел, можно выделить сходящуюся подпоследовательность.
.
Теорема (Вейерштрасс). Любая монотонная ограниченная последовательность имеет предел.
Доказательство.Докажем теорему для монотонной возрастающей последовательности  . Докажем, что точная верхняя граница для последовательности
. Докажем, что точная верхняя граница для последовательности  и будет ее пределом.
и будет ее пределом.
Действительно, по определению точной верхней границы

Кроме того, какое бы ни взять число  , найдется такой номер
, найдется такой номер  , что
, что

Так как последовательность монотонна, то при  будет
будет  , а значит, и
, а значит, и  и выполняются неравенства
и выполняются неравенства

откуда и следует, что  .
.
Эта замечательная теорема дает достаточные условия существования предела. Из нее, например, следует, что последовательность площадей правильных  -угольников, вписанных в окружность единичного радиуса, имеет предел, так как является монотонно возрастающей и ограниченной сверху. Предел этой последовательности обозначается
-угольников, вписанных в окружность единичного радиуса, имеет предел, так как является монотонно возрастающей и ограниченной сверху. Предел этой последовательности обозначается  .
.
С помощью предела монотонной ограниченной последовательности определяется играющее большую роль в математическом анализе число  - основание натуральных логарифмов:
- основание натуральных логарифмов:
 . Некоторые замечательные пределы.
. Некоторые замечательные пределы. 
