Ограниченные и неограниченные последовательности

1. Последовательность 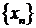называется ограниченной сверху, если 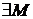такое, что для любого 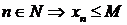. При этом число М называется верхней границей последовательности

2. Последовательность 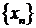называется ограниченной снизу, если 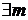такое, что для любого 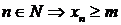. Число m называется нижней границей последовательности.

3. Последовательность 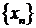называется ограниченной, если она ограничена и сверху и снизу, то есть 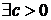такое, что 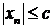для любого 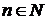. Заметим, что в данном определении c=max{|m|,|M|}.

Последовательность 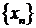называется неограниченной, если 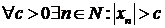Неограниченная последовательность может быть односторонне ограниченной, то есть ограниченной или сверху, или снизу. Пример неограниченной сверху последовательности: x_n = n.

Пример .

1. 1,2,...,n,... — ограничена снизу, но неограничена сверху;

2. {1/n} – ограничена, так как ;

{(-1)ⁿ} – ограничена

Теорема 1. Любая ограниченная сверху последовательность имеет наименьшую верхнюю границу U.
Теорема 2. Любая ограниченная снизу последовательность имеет наибольшую нижнюю границу L.

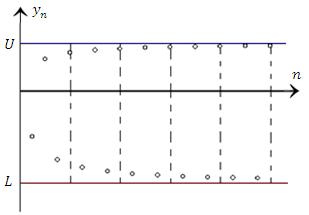
Рис. 3. 2.Наименьшая верхняя U и наибольшая нижняя границы L последовательности показаны горизонтальными линиями, расположенными вверху и внизу соответственно.

Свойства ограниченных последовательностей

Ограниченная сверху числовая последовательность имеет бесконечно много верхних граней.

Ограниченная снизу числовая последовательность имеет бесконечно много нижних граней.

Ограниченная последовательность имеет по крайней мере одну предельную точку.

У ограниченной последовательности существуют верхний и нижний пределы.

Для любого наперёд взятого положительного числа ε все элементы ограниченной числовой последовательности 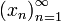, начиная с некоторого номера, зависящего от ε, лежат внутри интервала .

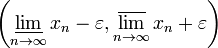Если за пределами интервала лежит лишь конечное число элементов ограниченной числовой последовательности 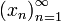, то интервал 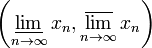содержится в интервале .

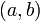Справедлива теорема Больцано — Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность

3.6. определение подпоследовательности

Как мы уже знаем последовательность это функция, заданная на множестве натуральных чисел. Если вместо множества всех натуральных чисел взять некоторое его бесконечное подмножество n_k, k = 1,2,..., n_k<n_k+1, то получим подпоследовательность 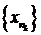. Иными словами, подпоследовательность получается из последовательности удалением конечного или счётного числа элементов. Таких подпоследовательностей можно выделить из данной последовательности бесконечное множество.

Пример.

x_n = {n}=1,2,3,...,n,… – последовательность натуральных чисел,.

x_nk = {1,3,...,2n-1,...} подпоследовательность нечетных чисел

Теорема.

Если последовательность {x_n} сходится и ее предел равен a, то любая ее подпоследовательность также сходится и имеет тот же самый предел.

Если {x_n} – бесконечно большая последовательность, то любая ее подпоследовательность есть также бесконечно большая.