Ограниченные и неограниченные множества. Конечные и бесконечные множества

Множества по количеству элементов могут быть конечными и бесконечными

Рассмотрим произвольное бесконечное множество вещественных чисел, оно може быть задано любым образом. Такими

Множествами являются, например, множество натуральных чисел, множество правильных дробей, множество вещественных чисел между 0 и 1, множество корней уравнения sin x = ½ и т.п.

Любое из чисел множества мы обозначим через х , Само множество обозначим через Х.

Определения 7.3.

Если для множества Х существует такое число М, что для всех х≤М, то множество Х называется ограниченным сверху (числом М), а само М называется верхней границей Х. Например, множество натуральных дробей ограничено сверху числом 1 (и вообще любым числом, больше или равным 1), натуральный ряд сверху неограничен

Аналогично определяется ограниченное снизу множество и нижняя граница

Ограниченное сверху (снизу) множество может быть при этом как ограничено, так и неограниченно снизу (сверху). Так, множество правильных дробей ограничено и сверху и снизу, а натуральный ряд ограничен снизу, но не сверху.

Если множество сверху (снизу) неограниченно, то за его верхнюю (нижнюю) границу принимают «несобственное» число 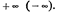Относительно этих «несобственных» или «бесконечных» чисел мы считаем, что 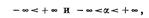каково бы ни было вещественное число α.

Множество , ограниченное и сверху и снизу, называется (просто) ограниченным.

Если множество ограничено сверху, т.е. имеет конечную верхнюю границу М, то одновременно оно имеет бесконечное множество верхних границ (так как, например, любое число >М, очевидно, также будет верхней границей). Из всех верхних границ наибольший интерес представляет наименьшая (она же точная верхняя граница, верхняя грань, супремум множества Х, supX (от латинского supremum - наибольший))

Аналогично определяется точня нижняя граница (нижняя грань, инфинум множества Х, inf X (от infinum – наименьший))

Определение ‘

Число β называется верхней гранью числового множества X, если:

2’ ) для любого ε>0 существует такой 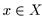, что x > β - ε

Рис. 7.3(1)

Для α=inf X определение ‘ сформулируйте сами рис. 7.3(2).

Рис. 7.3(2)

Пример.

Пусть 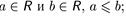; тогда

sup [a, b] = sup (а, b) = b, inf [а, b] = inf (а, b) = а.

Эти примеры показывают, в частности, что нижняя и верхняя грани могут как принадлежать, так и не принадлежать самому множеству.

В силу самого своего определения верхняя и нижняя грани множества единственны. В самом деле, если в некотором множестве, принадлежащем даже расширенной числовой прямой 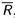, существует наименьший (наибольший) элемент, то он единственен, так как из двух разных элементов множества больший из них не может быть наименьшим элементом, а меньший — наибольшим.

Всегда ли ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) границу? Действительно, так как верхних (нижних) границ бесконечно много, а среди бесконечного множества чисел не всегда найдется наибольшее (наименьшее, то существование супремума (инфинума) требует специального доказательства.

Теорема 7.3(1)

Всякое ограниченное сверху непустое множество имеет верхнюю грань, а всякое ограниченное снизу непустое – нижнюю.

Доказательство

Пусть непустое числовое множество А ограничено сверху, В - множество всех чисел, ограничивающих сверху множество А. Если 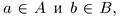то из определения числа, ограничивающего сверху

множество, следует, что a≤b. Следовательно, по свойству непрерывности действительных чисел существует такое число β, что для всех 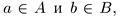будет выполняться неравенство a≤β≤b. Неравенство 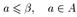, означает, что число β ограничивает сверху множество А, а неравенство 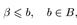— что число β является наименьшим среди всех чисел, ограничивающих сверху множество А. Следовательно, β= sup A.

Аналогично доказывается, что ограниченное снизу числовое множество имеет нижнюю грань.

Замечание 7.3.

Если числовое множество X неограничено сверху, то у него не существует верхней грани. В этом случае по определению полагаем, что верхней гранью множества X является :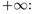

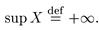
Аналогично для инфинума.

Натуральные числа

Определение 4.4.

Числа вида

2 = 1+1

3 = 2+1

и т.д.

называются натуральными и их множество обозначается N

Множество натуральных чисел обладает следующим характеристическим свойством:

Если:

Теорема 7.4.

Множество натуральных чисел неограниченно сверху

Доказательство

Докажите методом от противного, используя определение верхней грани