Извлечение корня из комплексного числа
Корень n-ой степени из комплексного числа 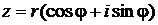 извлекается по формуле
извлекается по формуле
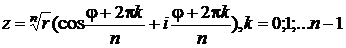 .
.
Значения 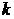 , отличные от указанных в этой формуле, дадут те же значения
, отличные от указанных в этой формуле, дадут те же значения 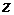 , которые можно получить при
, которые можно получить при 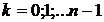 .
.
Пример. Найдите корни уравнения  .
.
Решение. Запишем число 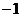 в тригонометрической форме:
в тригонометрической форме:
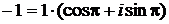 ,
,
то есть 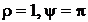 . Тогда
. Тогда
 .
.
При 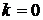 получим:
получим:
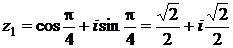 .
.
При 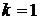 получим:
получим:
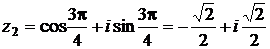 .
.
При 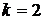 получим:
получим:
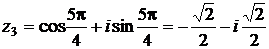 .
.
При 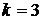 получим:
получим:
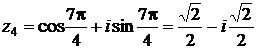 .
.
Ответ: 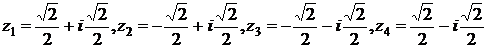 .
.
Образец выполнения контрольной работы
1. Даны матрицы 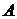 и
и 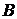 . Вычислить матрицу
. Вычислить матрицу 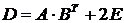 .
.
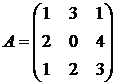 ,
, 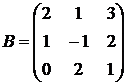 .
.
Решение. Транспонируем матрицу 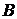 :
:
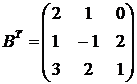 .
.
Найдем произведение матриц 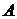 и
и 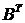 :
:
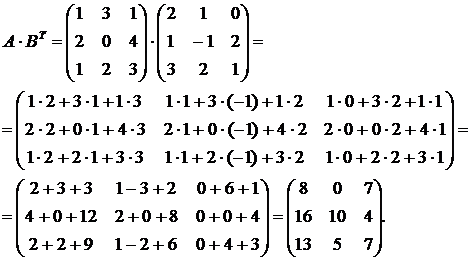
Следовательно, искомая матрица 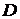 будет равна:
будет равна:
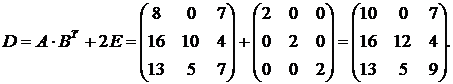
Ответ: 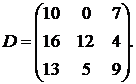
2. Вычислить определитель четвертого порядка:
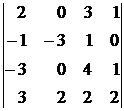 .
.
Решение. Разложим данный определитель по элементам второго столбца (т. к. второй столбец содержит наибольшее количество нулей):
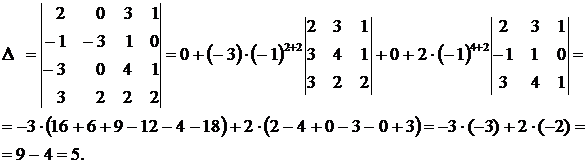
Ответ: 5.
3. Найти матрицу, обратную данной:
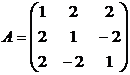 .
.
Решение.
1) Вычислим определитель матрицы 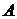 :
:
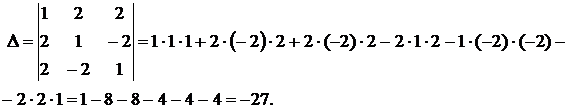
Поскольку определитель данной матрицы отличен от нуля, следовательно, обратная матрица существует.
2) Найдем матрицу, транспонированную к 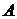 :
:
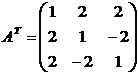 .
.
3) Вычислим алгебраические дополнения к транспонированной матрице:
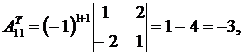
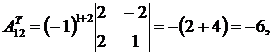
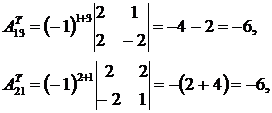
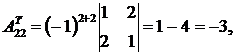
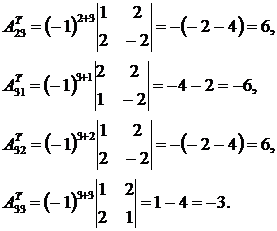
4) Найдем обратную матрицу:
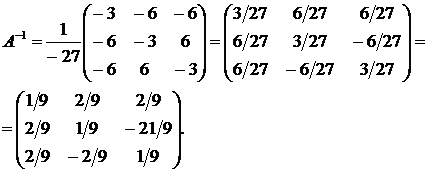
Ответ: 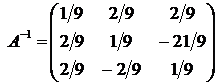 .
.
4. Решить систему линейных уравнений а) методом Крамера,
б) методом Гаусса:
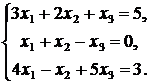
Решение.
а) Решим систему методом Крамера:
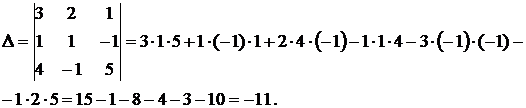
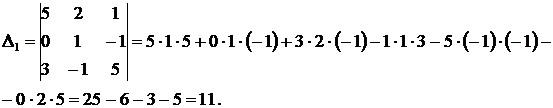
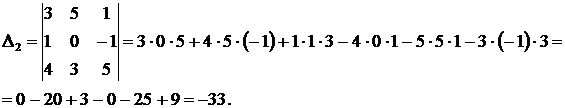
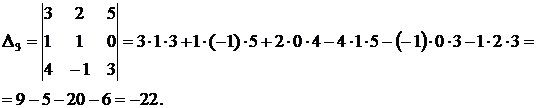
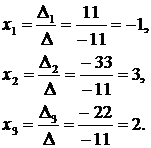
Ответ: 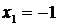 ,
, 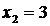 ,
, 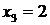 .
.
б) Решим систему методом Гаусса:
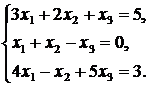
Составим расширенную матрицу данной системы и приведем ее к ступенчатому виду:



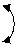
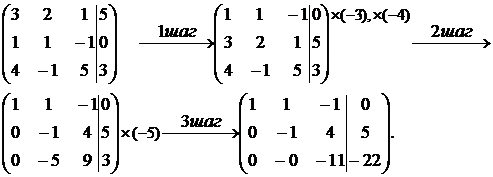
Вернемся к системе уравнений, соответствующей последней матрице:
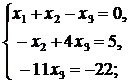
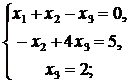
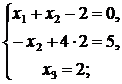
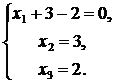
Ответ: 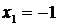 ,
, 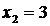 ,
, 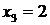 .
.
5. Вычислить 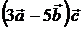 , если
, если 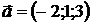 ,
, 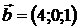 ,
, 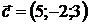 .
.
Решение.
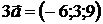 ,
,
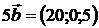 ,
,
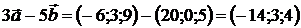 .
.
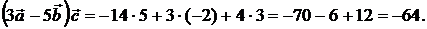
Ответ: 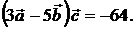
6. Даны вектора 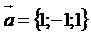 ,
, 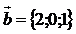 ,
, 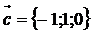 . Вычислить векторное произведение
. Вычислить векторное произведение 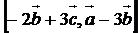 .
.
Решение.
Сначала определим координаты векторов 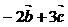 и
и 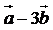 :
:
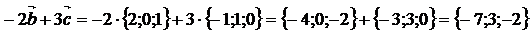 .
.
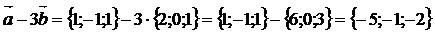 .
.
Тогда векторное произведение полученных векторов:
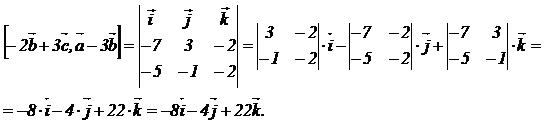
Ответ. 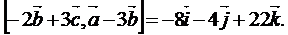
7. Даны вектора 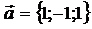 ,
, 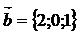 ,
, 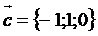 ,
, 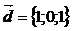 . Вычислить смешанное произведение векторов
. Вычислить смешанное произведение векторов 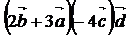 .
.
Решение.
Сначала определим координаты векторов 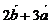 и
и 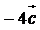 :
:
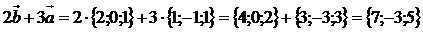 ,
,
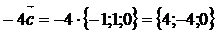 .
.
Тогда смешанное произведение векторов 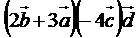 :
:
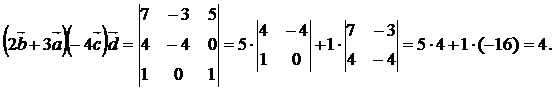
Ответ. 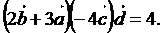
8. Для треугольника с вершинами 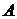 ,
, 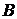 ,
, 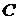 найти:
найти:
а) уравнение стороны 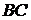 ;
;
б) длину высоты 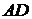 ;
;
в) уравнение высоты 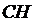 .
.
Решение.
а) Уравнение стороны 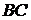 найдем по формуле уравнения прямой, проходящей через две точки:
найдем по формуле уравнения прямой, проходящей через две точки:
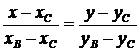
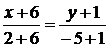
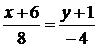
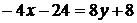
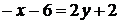
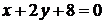 .
.
б) Высота 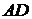 – это перпендикуляр к стороне
– это перпендикуляр к стороне 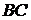 .
.
Тогда длина высоты 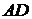 это расстояние от точки
это расстояние от точки 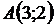 до прямой
до прямой 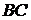 :
: 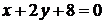 , которое можно вычислить по формуле:
, которое можно вычислить по формуле:
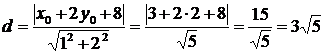 .
.
в) Высота 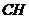 – это прямая, перпендикулярная прямой
– это прямая, перпендикулярная прямой 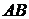 , проходящая через точку
, проходящая через точку 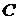 . Для этого найдем уравнение прямой
. Для этого найдем уравнение прямой 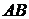 по формуле:
по формуле:
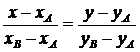 ,
,
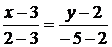 ,
,
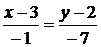 ,
,
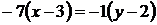 ,
,
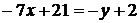 ,
,
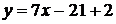 ,
,
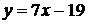 .
.
Угловой коэффициент прямой 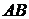 равен
равен 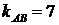 , поэтому угловой коэффициент перпендикуляра
, поэтому угловой коэффициент перпендикуляра 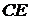 будет равен
будет равен 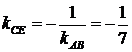 .
.
Уравнение перпендикуляра найдем по формуле: 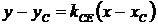 ,
,
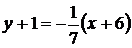 ,
,
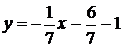 ,
,
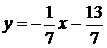 ,
,
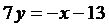 ,
,
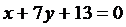 .
.
Ответ: а) 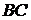 :
: 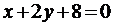 , б)
, б) 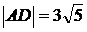 ; в)
; в) 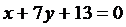 .
.
9. Даны комплексные числа 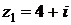 и
и 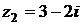 .
.
а) Вычислить 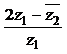 .
.
Решение. 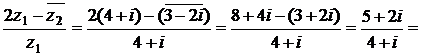
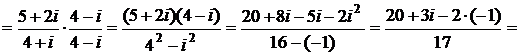
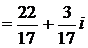 .
.
Ответ: 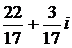 .
.
б) Вычислить корень 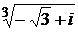 .
.
Решение. Запишем число 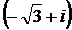 в тригонометрической форме:
в тригонометрической форме:
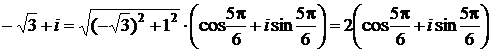 ,
,
то есть 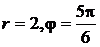 . Тогда
. Тогда 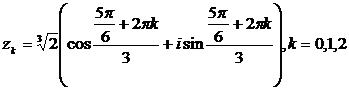 .
.
При 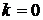 получим:
получим:
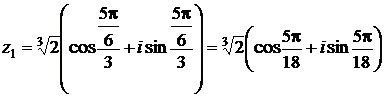 .
.
При 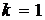 получим:
получим:
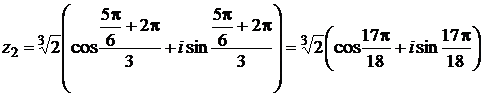 .
.
При 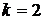 получим:
получим:
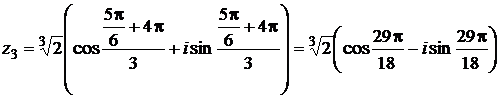 .
.
Ответ:
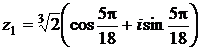 ,
, 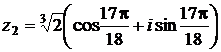 ,
, 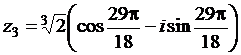 .
.
Задания контрольной работы
1. Даны матрицы 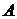 и
и 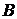 . Вычислить матрицу
. Вычислить матрицу 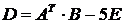
| Номер варианта | А | В |
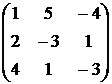 | 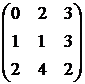 | |
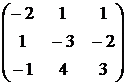 | 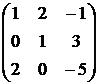 | |
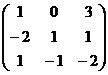 | 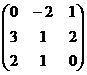 | |
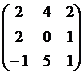 | 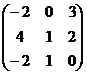 | |
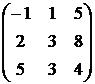 | 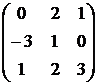 | |
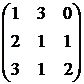 | 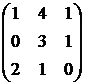 | |
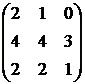 | 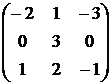 | |
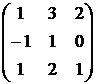 | 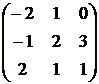 | |
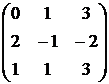 | 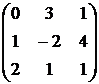 | |
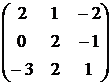 | 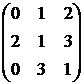 |
2*. Вычислить определитель четвертого порядка:
1) 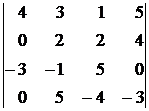 , 2)
, 2) 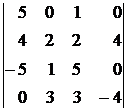 , 3)
, 3) 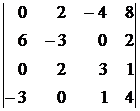 ,
,
4) 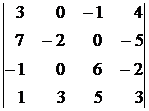 , 5)
, 5) 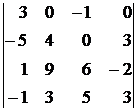 , 6)
, 6) 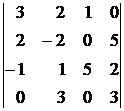 ,
,
7) 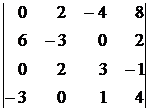 , 8)
, 8) 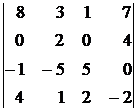 , 9)
, 9) 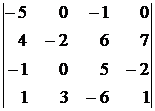 ,
,
10) 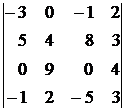 .
.
3. Найти обратную матрицу:
1) 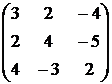 , 2)
, 2) 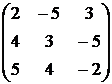 , 3)
, 3) 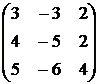 ,
,
4) 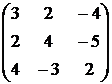 , 5)
, 5) 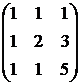 , 6)
, 6) 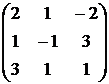 ,
,
7) 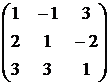 , 8)
, 8) 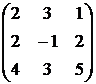 , 9)
, 9) 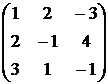 ,
,
10) 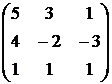 .
.
4. Решить систему линейных уравнений а) методом Крамера,
б)* методом Гаусса:
1) 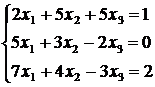 , 2)
, 2) 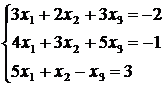 ,
,
3) 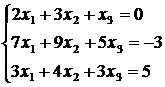
 , 4)
, 4) 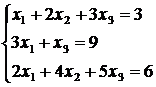 ,
,
5) 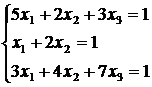 , 6)
, 6) 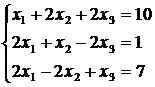 ,
,
7) 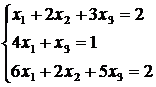 8)
8) 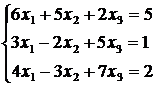 ,
,
9) 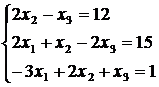 10)
10) 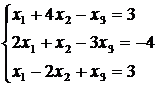 .
.
5. Вычислить скалярное произведение, если 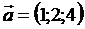 ,
, 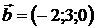 ,
, 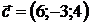 .
.
1) 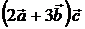 , 2)
, 2) 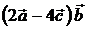 , 3)
, 3) 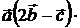 ,
,
4) 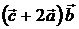 , 5)
, 5) 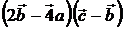 , 6)
, 6) 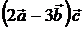 ,
,
7) 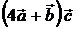 , 8)
, 8) 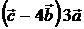 , 9)
, 9) 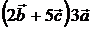 ,
,
10) 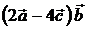 .
.
6.Даны вектора 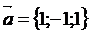 ,
, 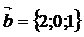 ,
, 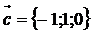 . Вычислить векторное произведение.
. Вычислить векторное произведение.
1) 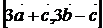 ;2)
;2) 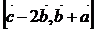 ;3)
;3) 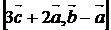 ;
;
4) 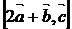 ; 5)
; 5) 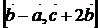 ; 6)
; 6) 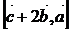 ;
;
7) 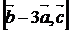 ; 8)
; 8) 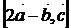 ; 9)
; 9) 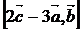 ;
;
10) 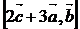 .
.
7.Даны вектора 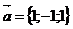 ,
, 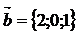 ,
, 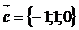 ,
, 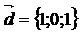 . Вычислить смешанное произведение векторов:
. Вычислить смешанное произведение векторов:
1) 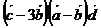 ; 2)
; 2) 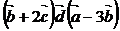 ; 3)
; 3) 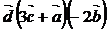 ;
;
4) 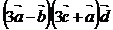 ; 5)
; 5) 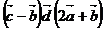 ; 6)
; 6) 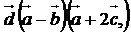 ;
;
7) 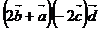 ; 8)
; 8) 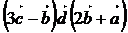 ; 9)
; 9) 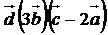 ;
;
10) 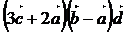 .
.
8. Для треугольника с вершинами 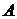 ,
, 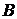 ,
, 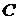 найти:
найти:
а) уравнение стороны 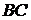 ;
;
б) длину высоты 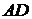 ;
;
в) уравнение высоты 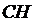 .
.
| Номер варианта | 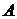 | 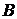 | 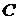 | Номер варианта | 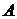 | 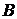 | 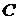 |
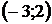 | 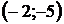 | 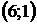 | 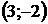 | 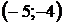 | 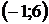 | ||
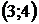 | 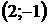 | 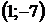 | 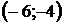 | 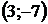 | 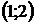 | ||
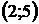 | 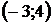 | 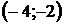 | 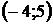 | 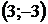 | 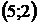 | ||
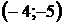 | 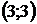 | 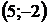 | 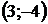 | 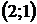 | 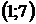 | ||
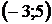 | 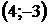 | 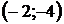 | 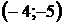 | 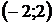 | 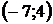 |
9. а)
1) Даны комплексные числа 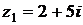 ,
, 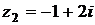 . Вычислить
. Вычислить 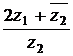 .
.
2) Даны комплексные числа 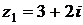 и
и 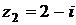 . Вычислить
. Вычислить 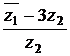 .
.
3) Даны комплексные числа 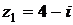 и
и 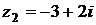 . Вычислить
. Вычислить 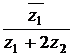 .
.
4) Даны комплексные числа 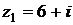 и
и 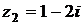 . Вычислить
. Вычислить 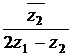 .
.
5) Даны комплексные числа 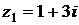 и
и 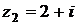 . Вычислить
. Вычислить 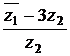 .
.
6) Даны комплексные числа 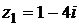 и
и 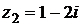 . Вычислить
. Вычислить 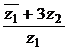 .
.
7) Даны комплексные числа 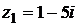 и
и 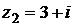 . Вычислить
. Вычислить 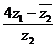 .
.
8) Даны комплексные числа 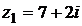 и
и 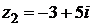 . Вычислить
. Вычислить 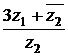 .
.
9) Даны комплексные числа 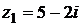 и
и 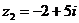 . Вычислить
. Вычислить 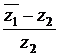 .
.
10) Даны комплексные числа 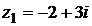 и
и 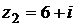 . Вычислить
. Вычислить 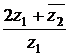 .
.
б) * Извлечь корень из комплексного числа:
1) 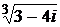 ; 2)
; 2) 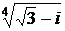 ; 3)
; 3) 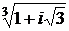 ;
;
4) 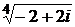 ; 5)
; 5) 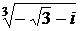 ; 6)
; 6) 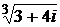 ;
;
7) 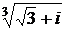 ; 8)
; 8) 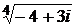 ; 9)
; 9) 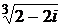 ;
;
10) 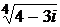 .
.
Учебно-методическое обеспечение
Основная литература:
1. Высшая математика для экономистов : учебник / под ред. Н. Ш. Кремера. – 3-е изд. – М. : ЮНИТИ-ДАНА, 2014. – 479 с.
2. Шипачев, В. С. Высшая математика. Полный курс : учебник / В. С. Шипачев ; под ред. А. Н. Тихонова. – 4-е изд., испр. и доп. – М. : Юрайт, 2014. – 607 с.
3. Ячменев, Л. Т. Высшая математика [Электронный ресурс] : учебник / Л. Т. Ячменев. – М. : РИОР : Инфра-М, 2013. – 752 с. – Режим доступа : http://znanium.сom.
Дополнительная литература:
4. Виленкин, И. В. Высшая математика : [учеб. пособие] / И. В. Виленкин, В. М. Гробер, О. В. Гробер. – Ростов н/Д. : Феникс, 2011. – 302 с.
5. Журбенко, Л. Н. Математика в примерах и задачах : учеб. пособие / Л. Н. Журбенко. – М. : ИНФРА-М, 2009. – 373 с.
6. Лурье, И. Г. Высшая математика [Электронный ресурс] : практикум / И. Г. Лурье, Т. П. Фунтикова. – М. : Вузовский учебник : ИНФРА-М, 2013. – 160 с. – Режим доступа : http://znanium.сom.
7. Математика : учеб. пособие / Ю. М. Данилов, Л. Н. Журбенко, Г. А. Никонова [и др.]. – М. : ИНФРА-М, 2009. – 496 с.
8. Туганбаев, А. А. Задачи по высшей математике для психологов [Электронный ресурс] / А. А. Туганбаев. – 3-e изд., исправ. и доп. – М. : Флинта, 2011. – 320 с. – Режим доступа : http://znanium.сom.
9. Турецкий, В. Я. Математика и информатика : учебник / В. Я. Турецкий. – 3-е изд., перераб. и доп. – М. : ИНФРА-М, 2012. – 558 с.
10. Шипачев, В. С. Задачник по высшей математике : учеб. пособие / В. С. Шипачев. – 7-е изд., стер. – М. : Высшая школа, 2007. – 304 с.
