Действия с векторами в координатах
В первой части урока мы рассматривали правила сложения векторов и умножения вектора на число. Но рассматривали их с принципиально-графической точки зрения. Посмотрим, как данные правила работают аналитически – когда заданы координаты векторов:
1) Правило сложения векторов. Рассмотрим два вектора плоскости 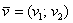 и
и 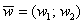 . Для того, чтобы сложить векторы, необходимо сложить их соответствующие координаты:
. Для того, чтобы сложить векторы, необходимо сложить их соответствующие координаты: 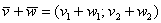 . Как просто. На всякий случай запишу частный случай – формулу разности векторов:
. Как просто. На всякий случай запишу частный случай – формулу разности векторов: 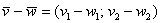 . Аналогичное правило справедливо для суммы любого количества векторов, добавим например, вектор
. Аналогичное правило справедливо для суммы любого количества векторов, добавим например, вектор 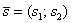 и найдём сумму трёх векторов:
и найдём сумму трёх векторов: 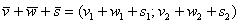
Если речь идёт о векторах в пространстве, то всё точно так же, только добавится дополнительная координата. Если даны векторы 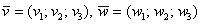 , то их суммой является вектор
, то их суммой является вектор 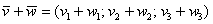 .
.
2) Правило умножения вектора на число. Ещё проще! Для того чтобы вектор 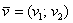 умножить на число
умножить на число 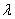 , необходимо каждую координату данного вектора умножить на число
, необходимо каждую координату данного вектора умножить на число 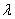 :
:
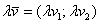 .
.
Для пространственного вектора 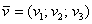 правило такое же:
правило такое же:
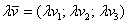
Приведённые факты строго доказываются в курсе аналитической геометрии.
Примечание: Данные правила справедливы не только для ортонормированных базисов 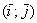 ,
, 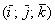 но и для произвольного аффинного базиса плоскости или пространства. Более подробно о базисах читайте в статье Линейная (не) зависимость векторов. Базис векторов.
но и для произвольного аффинного базиса плоскости или пространства. Более подробно о базисах читайте в статье Линейная (не) зависимость векторов. Базис векторов.
Пример 7
Даны векторы 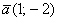 и
и 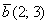 . Найти
. Найти 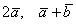 и
и 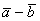
Решение чисто аналитическое:
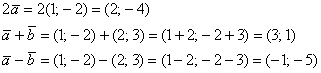
Ответ: 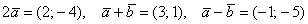
Чертеж в подобных задачах строить не надо, тем не менее, геометрическая демонстрация будет весьма полезной. Если считать, что векторы заданы в ортонормированном базисе 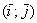 , то графическое решение задачи будет таким:
, то графическое решение задачи будет таким:
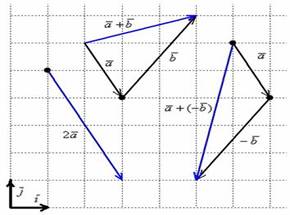
Коль скоро речь идет только о векторах в ортонормированном базисе, то оси рисовать не обязательно. Достаточно начертить базисные векторы, причём, где угодно. Ну, и координатную сетку для удобства. Строго говоря, ранее я допустил небольшой огрех – в некоторых чертежах урока тоже можно было не чертить декартову прямоугольную систему координат. Векторам она не нужна, им нужен базис. Впрочем, лучше всегда рисуйте, а то напугаете всех своими знаниями =)
Как видите, графический способ решения привёл к тем же результатам, что и аналитический способ решения. Ещё раз заметьте свободу векторов: любую из трёх «конструкций» можно переместить в любую точку плоскости.
Для векторов в пространстве можно провести аналогичные выкладки. Но там чертежи строить значительно сложнее, поэтому ограничусь аналитическим решением (на практике, собственно, бОльшего и не надо):
Пример 8
Даны векторы 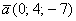 и
и 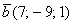 . Найти
. Найти 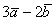 и
и 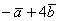
Решение:Для действий с векторами справедлив обычный алгебраический приоритет: сначала умножаем, потом складываем:
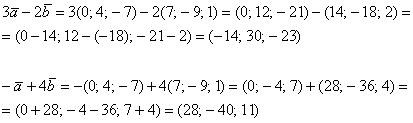
Ответ: 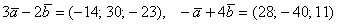
И в заключение занятный пример с векторами на плоскости:
Пример 9
Даны векторы 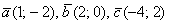 . Найти
. Найти 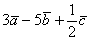 и
и 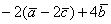
Это задача для самостоятельного решения.
Какой вывод? Многие задачи аналитической геометрии прозрачны и просты, главное, не допустить вычислительных ошибок. Следующие рекомендуемые к изучению уроки:
!!! Скалярное произведение векторов
Линейная (не) зависимость векторов. Базис векторов
Векторное и смешанное произведение векторов
Это, так скажем, вектор-минимум студента =)
Любите векторы, и векторы полюбят вас!
Решения и ответы:
Задание: 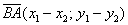 ,
, 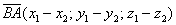
Пример 2: Решение:
а)
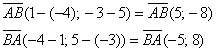
б)
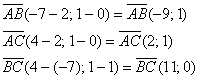
в)
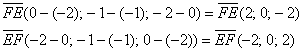
г)
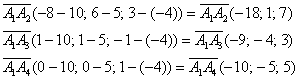
Пример 4: Решение:
По соответствующей формуле: 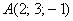 и
и 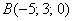
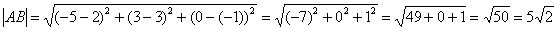
Ответ: