Операции над векторами в координатах.

Пусть два вектора заданы своими разложениями по ортам в декартовой системе координат

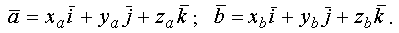
Тогда скалярное произведение

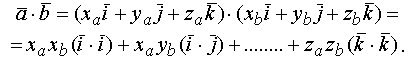
Помня, что от перестановки сомножителей скалярного произведения результат не меняется, получим

Учитывая эти результаты, найдем

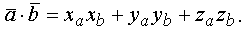
Скалярное произведение векторов, заданных проекциями в декартовой системе координат, равно сумме произведений одноименных координат.

Подчеркнем еще раз, что эта формула справедлива только в ортонормированном базисе.

Косинус угла между векторами определится выражением

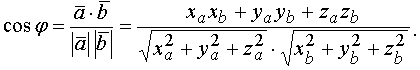
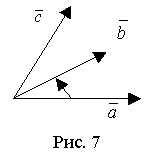
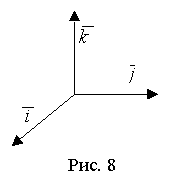
Упорядоченная тройка векторов 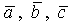называется правой, если наблюдателю, находящемуся на конце вектора , кратчайший поворот от 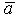к к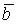ажется происходящим против часовой стрелки (рис. 7). В противном случае тройка векторов левая.

Например,

Тройки компланарных векторов не относятся ни к правым, ни к левым.

Векторным произведением вектора 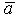на вектор 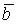называется третий вектор 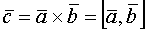определяемый следующим образом:
1) длина его равна площади параллелограмма, построенного на векторах 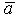и 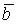, т.е.

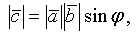
где φ - угол между векторам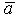и и ;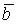
2) вектор 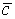перпендикулярен векторам 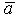и ;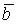
3) векторы 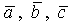после приведения к общему началу образуют правую тройку векторов.

Свойства векторного произведения:

Векторное произведение:

Пусть два вектора заданы своими разложениями по ортам в декартовой системе координат

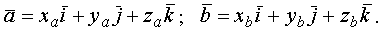
Найдем векторное произведение

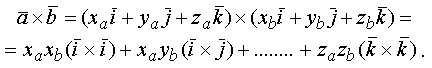
Помня, что от перестановки сомножителей векторного произведения результат меняет знак, получим

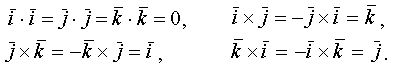
Учитывая эти результаты, найдем

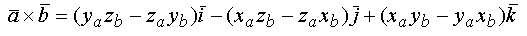
или

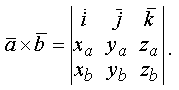
Т.о., вектор, получаемый в результате векторного произведения векторов, заданных своими координатами, получается из определителя, первой строкой которого являются координатные орты, вторая и третья строки состоят, соответственно, из координат первого и второго сомножителей.

Смешанным произведением трех векторов 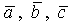называется число

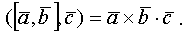
Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на этих векторах.

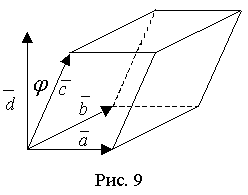Пусть 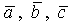правая тройка векторов (рис. 9). Действительно, объем параллелепипеда, построенного на векторах 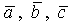, равен площади основания 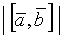на высоту 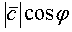. Здесь φ - угол между векторам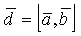и и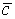

Знак смешанного произведения совпадает со знаком cos φ, и поэтому смешанное произведение положительно, когда тройка векторов правая, и отрицательно, если тройка векторов левая.

Если перемножаемые векторы лежат в одной плоскости (cos φ = 0), то 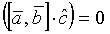- необходимое и достаточное условие компланарности векторов.

Пусть векторы заданы своими разложениями по ортам в декартовой системе координат

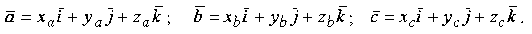
Из 3.6.2 известно, что

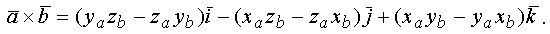
Скалярно умножим этот вектор на вектор 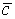и, учитывая свойства скалярного произведения, получим

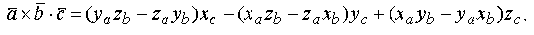
Это выражение может быть получено при вычислении определителя

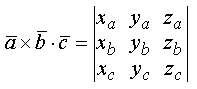
по элементам третьей строки, исходя из правила вычисления определителя.

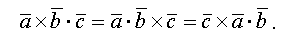
Поэтому смешанное произведение трех векторов обозначают как , не подчеркивая при этом, какая пара векторов умножается векторно.