Формула полной вероятности. Формула Бейеса
Если событие A может произойти только с одним из несовместных событий H1, H2,…, Hn, образующих полную группу, т.е.  , то вероятность события A может быть найдена по формуле полной вероятности:
, то вероятность события A может быть найдена по формуле полной вероятности:
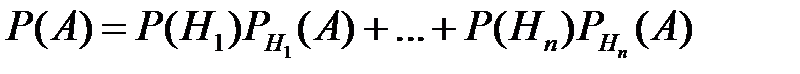 . (9)
. (9)
Так как заранее неизвестно, какое из событий H1, H2,…, Hn наступит, то их называют гипотезами.
Пример 11. В первой урне находится 5 белых и 3 черных шара. Во второй – 4 белых и 5 черных шара. Из первой урны во вторую наугад перекладывают два шара. После этого из второй урны вынимают сразу 4 шара. Какова вероятность того, что шары будут одного цвета?
Решение. По условиям данной задачи, результат второго испытания (т.е. вынимание шаров из второй урны) зависит от того, какие шары были переложены из первой урны. Здесь возможны три случая:
H1 = {оба шара белые},
H2 = {оба шара черные},
H3 = {один белый, один черный шар}.
Очевидно, что события H1, H2 и H3 несовместны и образуют полную группу. Их вероятности определим с помощью комбинаторики. Они равны
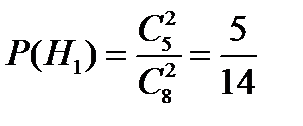 ,
, 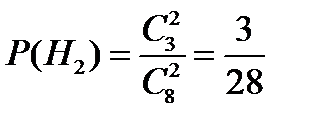 ,
, 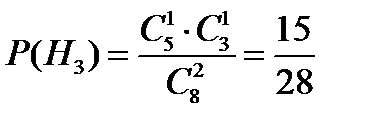 .
.
Условные вероятности события А = {шары одного цвета}, равны
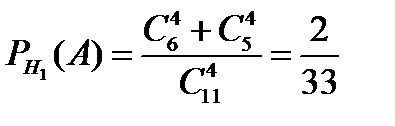 ,
, 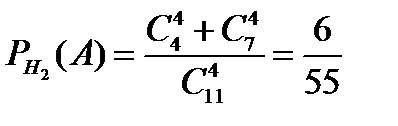 ,
, 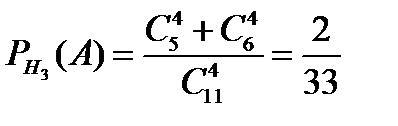 .
.
Применяя формулу полной вероятности, получим
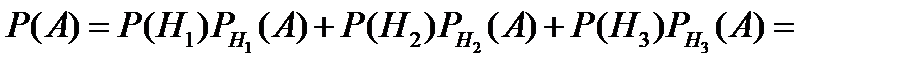
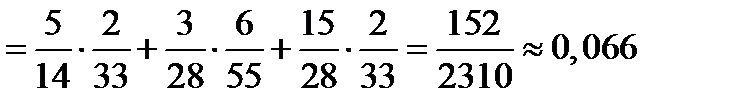
Пример 12. Вероятность того, что новый товар будет пользоваться спросом на рынке, если конкурент не выпустит в продажу аналогичный продукт, равна 0,67. Вероятность того, что товар будет пользоваться спросом при наличии на рынке конкурирующего товара, равна 0,42. Вероятность того, что конкурирующая фирма выпустит аналогичный товар на рынок в течение интересующего нас периода, равна 0,35. Чему равна вероятность того, что товар будет иметь успех?
Решение. Введем события: A = {товар будет иметь успех на рынке}, H1 = {конкурент выпустит в продажу аналогичный продукт}, H2 = {конкурент не выпустит в продажу аналогичный продукт}. Поскольку эти события несовместные и образуют полную группу, то 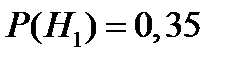 и
и 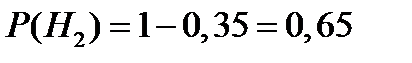 . По условию задачи
. По условию задачи 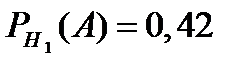 и
и 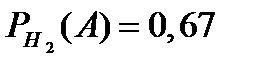 . В результате по формуле полной вероятности (1.14) находим
. В результате по формуле полной вероятности (1.14) находим
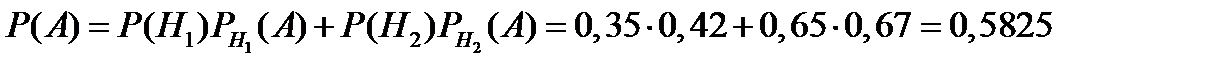 .
.
Пусть существует несколько предположений (несовместных гипотез) для объяснения некоторого события. Эти предположения проверяются при помощи опыта. Для проведения опыта бывает сложно определить вероятность этих предположений, поэтому им часто приписывают некоторые вероятности, которые называют априорными (до - опытными). Затем проводят опыт и получают информацию, на основании которой корректируют априорные вероятности. После проведения эксперимента вероятности гипотез могут измениться. В результате до - опытные вероятности заменяются после - опытными (апостериорными).
Переоценку первоначальных гипотез производят по формуле Бейеса:
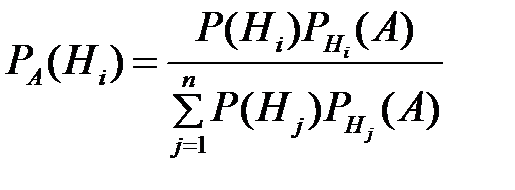 . (10)
. (10)
Пример 13.Два автомата производят детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго автомата. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84% деталей отличного качества. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь изготовлена первым автоматом.
Решение. Пусть A = {деталь изготовлена первым автоматом}. Определим гипотезы: H1 = {деталь изготовлена первым автоматом}, H2 = {деталь изготовлена вторым автоматом}. Поскольку производительность первого автомата вдвое больше производительности второго, то 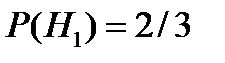 и
и 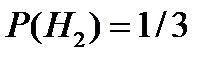 . По условию задачи
. По условию задачи 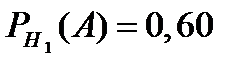 и
и 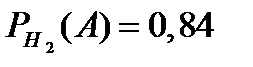 . По формуле полной вероятности (9) находим
. По формуле полной вероятности (9) находим
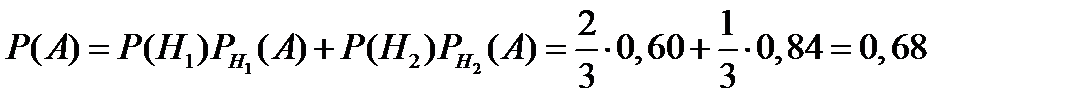
По формуле Бейеса находим: 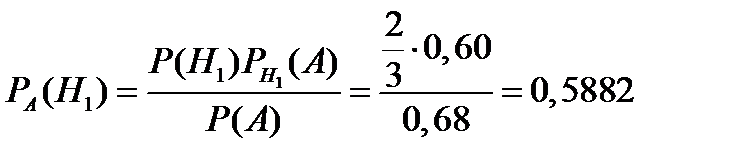 .
.
Т.е. с вероятностью 58,82% наудачу взятая деталь высшего сорта изготовлена первым автоматом.
Пример 14. Экономист-аналитик условно подразделяет экономическую ситуацию в стране на «хорошую», «посредственную» и «плохую» и оценивает вероятности для данного момента времени в 0,15, 0,70 и 0,15 соответственно. Некоторый индекс экономического состояния возрастает с вероятностью 0,7, когда ситуация в стране «хорошая», с вероятностью 0,4, когда ситуация «посредственная», и с вероятностью 0,1 когда ситуация «плохая». Пусть в настоящий момент времени индекс изменился. Какова вероятность того, что экономика страны на подъёме?
Решение. Пусть A = {индекс экономического состояния возрастает}. Определим гипотезы: H1 = {экономическая ситуация в стране «хорошая»}, H2 = {экономическая ситуация в стране «посредственная»}, H3 = {экономическая ситуация в стране «плохая»}. По условию задачи 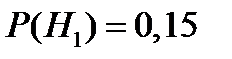 ,
, 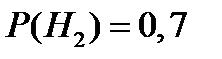 и
и 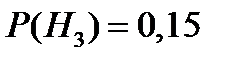 , а также
, а также 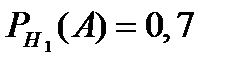 ,
, 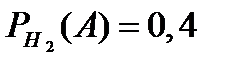 ,
, 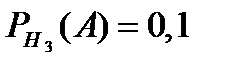 .
.
По формуле полной вероятности (9) находим
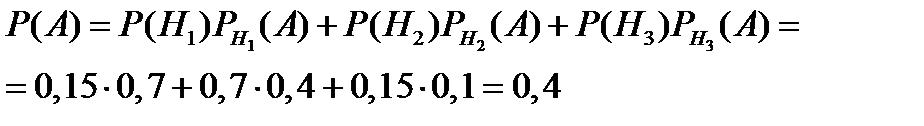

В результате по формуле Бейеса (10) получаем:
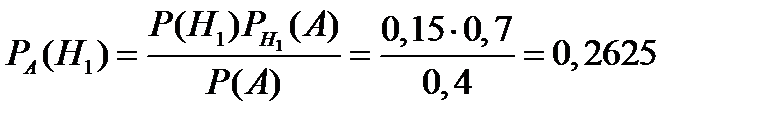 ,
,
т.е. вероятность того, что экономика страны на подъёме равна 26%.
Вопросы для самоконтроля
1.Из колоды вынимаются 4 карты с возвратом. Тогда вероятность того, что в руках окажутся 4 туза, равна…
1) 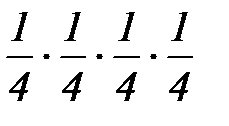 2)
2) 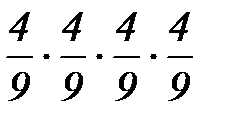 3)
3) 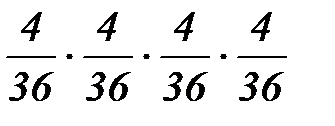 4)
4) 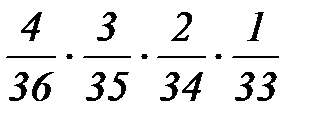
2.Вероятность рождения мальчика равна 0,52. Тогда вероятность того, что в семье из 3 детей будет 2 мальчика равна…
1) 0,389 2) 0, 567 3) 0, 73 4) 0,270
3. Собрание, на котором присутствуют 20 человек, в том числе 8 женщин, выбирают делегацию из 5 человек. Тогда вероятность того, что в делегацию войдут 3 женщины, равна…
1) 0, 238 2) 3/8 3) 2/12 4) 5/20
4.Брошены два игральных кубика. Тогда вероятность, что сумма выпавших очков будет равна 7, определится как…
1) 1/6 2) 5/6 3) 5/36 4) 8/36
5.Вероятность попадания в цель при отдельном выстреле равна 0,8, причем в 2% случаях бывают осечки. Тогда вероятность поражения цели равна…
1) 0, 016 2) 0, 784 3) 0, 86 4) 0,82
Ответы. 1) 3 вариант, 2) 1 , 3) 1 , 4) 1, 5) 2,
Задания для аудиторных занятий
1. В первой урне 8 белых и 2 черных шара. Во второй урне 7 белых и 3 черных шара. В третьей урне 5 белых и 5 черных шаров. Из наудачу взятой урны вынули один шар. Какова вероятность того, что этот шар черный?
2.Вероятность изготовления на станке-автомате нестандартной детали равна 0,02. Какова вероятность того, что среди шести наудачу взятых деталей окажется более четырех стандартных?
3..10 вариантов контрольных работ распределено среди 8 студентов. Тогда вероятность того, что варианты с номерами 1 и 2 не будут использованы равна….
4 .Прибор, установленный на борту самолета, может работать в двух режимах: в условиях нормального крейсерского полета и в условиях перегрузки при взлете и посадке. Крейсерский режим осуществляется в 80% всего полета, условия перегрузки – в 20%. Вероятность выхода прибора из строя за время полета в нормальном режиме равна 0,1, в условиях перегрузки – 0,4. Чему равна надежность прибора во время полета?
5. Вероятность сдать экзамен студентом равна 0,8. Тогда вероятность того, что студент его сдаст по крайней мере с третьей попытки равна…
6. Вероятность попадания в мишень при одном выстреле для данного стрелка равна 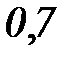 . Для вычисления вероятности того, что при 200 выстрелах мишень будет поражена 160 раз, следует использовать …
. Для вычисления вероятности того, что при 200 выстрелах мишень будет поражена 160 раз, следует использовать …
1 формулу полной вероятности 2 формулу Пуассона
3 локальную формулу Муавра-Лапласа 4 формулу Байеса
7.Вероятность попадания в цель при одном выстреле из орудия р=0,85. Найти вероятность того, что в цель попадет не менее двух снарядов, если будет сделано 3 выстрела
8 .Найти вероятность того, что при 4 испытаниях событие наступит ровно 2 раза, если вероятность его появления в каждом испытании равна 0,2
9 Торговый агент в среднем контактирует с восемью потенциальными покупателями в день. Из опыта ему известно, что вероятность того, что потенциальный покупатель совершить покупку, равна 0,15. Чему равна вероятность того, что у агента будут хотя бы две продажи в течение дня?
10. В установленном технологическом процессе фабрика выпускает в среднем 75% процентов изделий 1-го типа. Найти вероятность того, что в партии из 500 изделий окажется изделий 1-го типа: а) ровно 390; б) больше 370, но меньше 400.
11. Всхожесть семян определенного сорта растений равна 0,95. Найти вероятность того, что из 500 посаженых семян число проросших будет: 1) ровно 485; 2) не менее 470, но не более 480.
12. На склад поступает продукция трех фабрик. Продукция первой составляет 20%, второй – 46% и третьей – 34%. Процент брака для первой фабрики равен 3%, для второй – 1%, для третьей – 2%. Наудачу взятое изделие оказалось бракованным. Найти вероятность того, что оно произведено на первой фабрике.
13.Три группы студентов одновременно сдают письменно зачет, причем в первой группе находится 15 человек, во второй – 19 человек, в третьей – 25. Известно, что в среднем с первой попытки сдают зачет в первой группе 70% студентов, во второй и третьей – 60% и 40%, соответственно. Наудачу взятая работа оказалась зачтенной. Какова вероятность того, что эта работа из третьей группы?
Контрольное задание № 8
1. Для проверки собранной схемы последовательно послано три одиночных импульса. Вероятности прохождения каждого из них не зависят от того, прошли остальные или нет, и соответственно равны 0,8, 0,4 и 0,7. Определить вероятность того, что пройдут не менее двух посланных импульсов.
2. На начальном участке для мотоциклиста-гонщика имеются 3 препятствия, вероятность остановки на каждом из которых равна 0,1. Вероятность остановки на заключительном участке равна 0,7. Какова вероятность того, что мотоциклист доедет до финиша без единой остановки?
3. Вероятность наступления события в каждом опыте одинакова и равна 0,2. Опыты производятся последовательно до наступления события. Определить вероятность того, что понадобится не менее трех опытов.
4. Вероятность сдать экзамен студентом равна 0,8. Какова вероятность того, что студент сдаст экзамен по крайней мере с третьей попытки?
5. Предположим, что для одной торпеды вероятность попасть в цель равна 0,7. Какова вероятность того, что три торпеды потопят корабль, если для потопления нужно не менее двух попаданий в цель?
6. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,26. Найти вероятность поражения цели первым из орудий, если известно, что вероятность попадания в цель вторым орудием при одном выстреле равна 0,9.
7. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочнике соответственно равны 0,6, 0,8 и 0,9. Найти вероятность того, что формула содержится только в двух справочниках.
8. Разрыв электрической цепи может произойти вследствие выхода из строя элемента А или двух элементов В и С, которые выходят из строя независимо друг от друга соответственно с вероятностями 0,3, 0,2 и 0,1. Определить вероятность разрыва цепи.
9. Вероятность для данного спортсмена улучшить свой предыдущий результат с одной попытки равна 0,6. Определить вероятность того, что на соревнованиях спортсмен улучшит свой результат, если разрешается делать две попытки.
10. Вероятность поражения мишени, если по ней делают по одному выстрелу два стрелка, равна 0,82. Определить вероятность попадания в цель при одном выстреле для первого стрелка, если вероятность попадания для второго стрелка равна 0,7.
11. Бизнесмен забыл последнюю цифру номера телефона своего компаньона и набрал ее наугад. Определить вероятность того, что ему придется набирать номер не более трех раз, если известно, что последняя цифра была четной.
12. Система, состоящая из двух элементов типа А и трех элементов типа В, выходит из строя в случае, если отказывает хотя один элемент типа А или более одного элемента типа В. Найти надежность (вероятность безотказной работы) системы, если элементы независимы и вероятность безотказной работы элемента А равна 0,9, а элемента В равна 0,7.
13. На начальном участке для мотоциклиста-гонщика имеются 4 препятствия, вероятность остановки на каждом из которых равна 0,1. Вероятность остановки на заключительном участке равна 0,6. Какова вероятность того, что мотоциклист доедет до финиша без единой остановки?
14. Два стрелка, независимо друг от друга, делают по два выстрела, каждый по своей мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,6, а для второго – 0,7. Найти вероятность того, что выиграет первый стрелок, если выигравшим считается тот стрелок, в мишени которого будет больше пробоин
15. В ОТК поступают 4 детали. Вероятность того, что деталь бракованная равна 0,9. Проверка производится последовательно до обнаружения бракованной детали. Найти вероятность того, что будут проверены все 4 детали.
16. Одна из наиболее сложных проблем рыночных исследований – отказ потребителей отвечать на вопросы о потребительских предпочтениях, либо, если опрос проводится по месту жительства, – отсутствие их дома на момент опроса. Предположим, что исследователь рынка с вероятностью в 0,85 верит, что респондент согласится отвечать на вопросы анкеты, если окажется дома. Он также полагает, что вероятность того, что этот же человек будет дома, равна 0,7. Имея такие данные, оцените процент заполненных анкет..
17. Предположим, что 30% населения живет в области, охваченной коммерческим TV, рекламирующим две новые модели автомобилей; 45% населения охвачено радиорекламой. Также известно, что 10% населения слушает и радио и телерекламу. Если случайно отобрать человека, живущего в данной области, то чему будет равна вероятность того, что он знаком по крайней мере хотя бы с одной из рекламных передач фирмы?
18. Для рыночного исследования необходимо проведение интервью с людьми, которые добираются на работу общественным транспортом. В районе, где проводится исследование, 75% людей добираются на работу общественным транспортом. Если три человека согласны дать интервью, то чему равна вероятность того, что, по крайней мере, один из них добирается на работу общественным транспортом?
19. Уличный торговец предлагает прохожим иллюстрированную книгу. Из предыдущего опыта ему известно, что в среднем один из 65 прохожих, которым он предлагает книгу, покупает ее. В течение некоторого промежутка времени он предложил книгу 20 прохожим. Чему равна вероятность того, что он продаст им хотя бы одну книгу?
20. Иностранная фирма, производящая автомобили, интересуется российским рынком. Для изучения вкусов потенциальных покупателей проводится опрос, в котором выясняются наиболее желательные характеристики автомобиля. Предположим, что результаты опроса показали: 35% потенциальных покупателей в основном оценивают автомобиль по его техническим характеристикам, 50% – по его дизайну, 25% – считают важным и то, и другое. Основываясь на этой информации, ответьте, являются ли два вида предпочтений потенциальных покупателей независимыми друг от друга? Объясните почему.
15.1 Основные понятия и определения
Понятие случайной величины является одним из центральных понятий теории вероятностей. зависящее от случайных обстоятельств. Случайная величина характеризует все возможные результаты эксперимента с количественной стороны, однако, нельзя достоверно предсказать, какое именно значение при этом она примет.
Случайные величины могут быть дискретными и непрерывными.
Дискретной случайной величиной (ДСВ) называют величину, принимающую отдельные, изолированные значения с определенными вероятностями. Например, число зерен в колосках пшеницы, число студентов в различных группах и т.д.
Непрерывной случайной величиной (НСВ) называют величину, принимающую любое значение из некоторого конечного или бесконечного числового промежутка. Например, место попадания снаряда огнестрельного орудия и т.д.
Для описания дискретной СВ на практике используют ряд распределения вероятностей , когда каждому возможному значению случайной величины из полной группы ставится в соответствие своя вероятность. Егозаписывают в виде таблицы:
| X | x1 | 2 | … | xk |
| P | p1 | p2 | … | pk |
где выполнение равенства 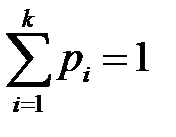 обязательно.
обязательно.
Вероятность попадания ДСВ в отрезок 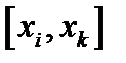 определяется как сумма соответствующих этому отрезку вероятностей:
определяется как сумма соответствующих этому отрезку вероятностей:
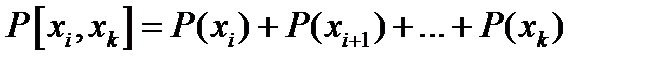 (1)
(1)
Для описания непрерывной СВ на практике используют плотность распределения вероятностей 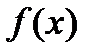 или функцией распределения F(x). Они обладают следующими свойствами:
или функцией распределения F(x). Они обладают следующими свойствами:
1. 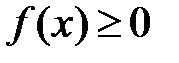 ,
, 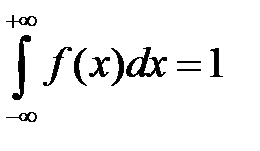 ;
;
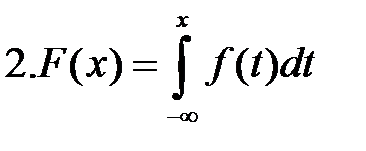
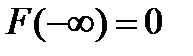
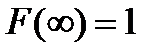
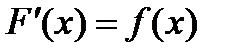
Эти функции не позволяют определить вероятность попадания случайной величины в конкретную точку, только в заданный промежуток (интервал). Её определяют по формуле 2:
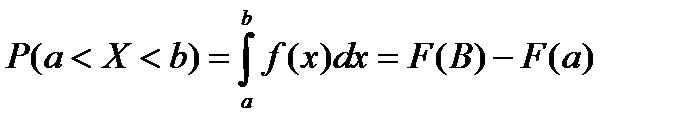 (2)
(2)
Пример 1. Монета брошена 3 раза. Случайная величина X – число появлений "орла". Составить ряд распределения. Найти вероятность того, что орел выпадет не более 2 раз.
Решение. Вероятность появления герба в каждом испытании равна p=1/2, а противоположного события – q=1/2. Возможные значения случайной величины X: x0=0, x1=1, x2=2, x3=3. По формуле Бернулли найдем вероятности этих возможных значений:
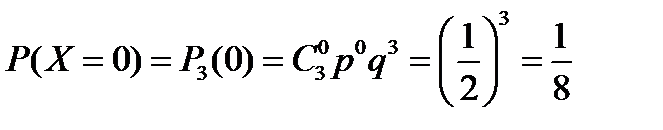 ,
,
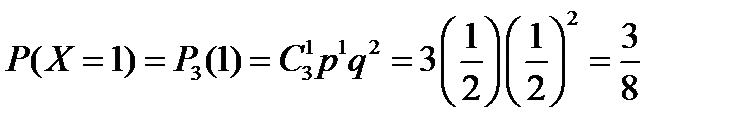 ,
,
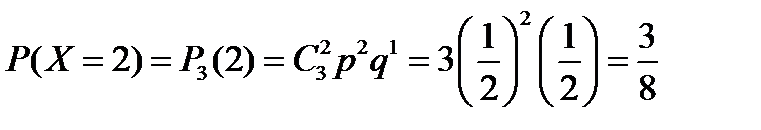 ,
,
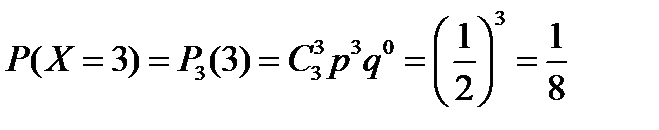 .
.
Таким образом, закон распределения случайной величины X можно записать в виде следующего ряда распределения:
| X | ||||
| P | 1/8 | 3/8 | 3/8 | 1/8 |
Проверка: 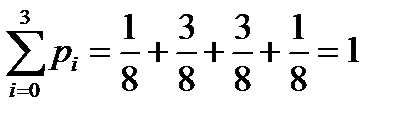
Вероятность того, что орел выпадет не более 2 раз, определим формуле 1: 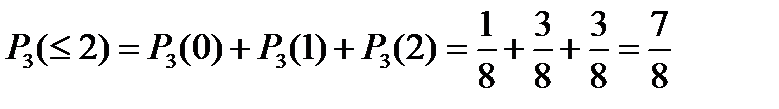
Пример 2. Непрерывная случайная величина задана плотностью распределения 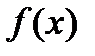
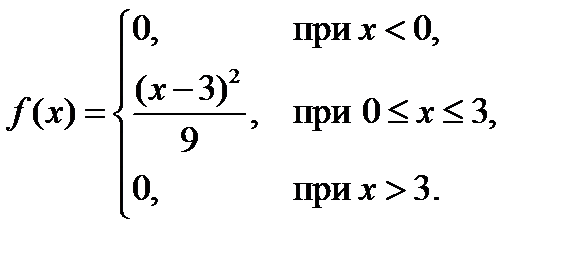
Найти функцию распределения F(x) и вероятность попадания НСВ в интервал (1;2).
Решение. Воспользуемся свойством 2 для F(x):
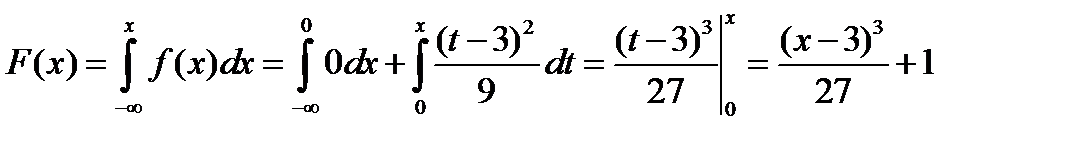 .
.
Таким образом, искомая функция распределения F(x) имеет вид
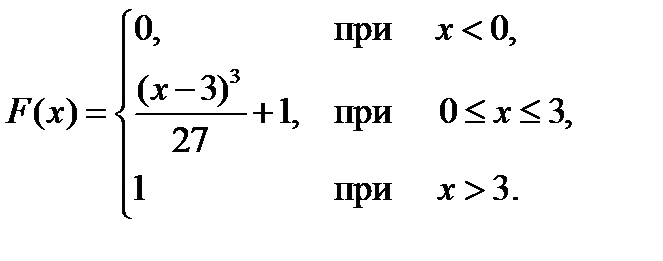
Для нахождения вероятности попадания случайной величины в интервал (1;2) воспользуемся формулой 2.
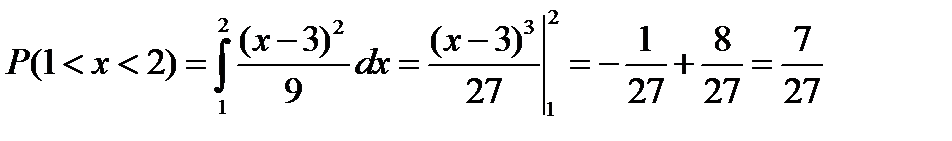 .
.
