Уравнение с разделяющимися переменными
Уравнение с разделенными переменными
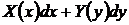 , (22)
, (22)
где функции 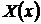 и
и 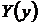 непрерывны, не имеют особых решений. Общий интеграл такого уравнения пишется сразу
непрерывны, не имеют особых решений. Общий интеграл такого уравнения пишется сразу
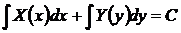 , (23)
, (23)
или в форме Коши
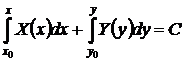 . (24)
. (24)
Если 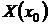 и
и 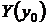 не равны нулю одновременно, то решение задачи Коши можно получить, полагая С = 0 в форме (24). Если же
не равны нулю одновременно, то решение задачи Коши можно получить, полагая С = 0 в форме (24). Если же 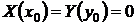 , то требуются дополнительные исследования, поскольку точка
, то требуются дополнительные исследования, поскольку точка 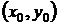 может оказаться особой точкой уравнения (22), а значит, единственное решение с начальными данными x0, y0 может не существовать.
может оказаться особой точкой уравнения (22), а значит, единственное решение с начальными данными x0, y0 может не существовать.
Уравнение с разделяющимися переменными. Дифференциальное уравнение
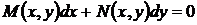 ,
,
в котором непрерывные функции  и
и  могут быть представлены в виде произведения функций, зависящих только от одного аргумента
могут быть представлены в виде произведения функций, зависящих только от одного аргумента
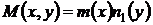 ,
, 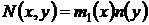 ,
,
то есть дифференциальное уравнение
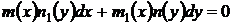 (25)
(25)
называется уравнением с разделяющимися переменными.
Предполагая, что 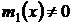 ,
, 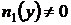 , путем деления на произведение
, путем деления на произведение 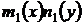 уравнение (25) приводится к уравнению с разделенными переменными
уравнение (25) приводится к уравнению с разделенными переменными
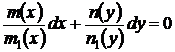 .
.
Общим интегралом этого уравнения, а следовательно, и уравнения (25), будет
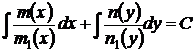 (26)
(26)
или
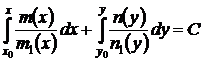 . (27)
. (27)
Предположение 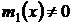 ,
, 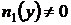 , может привести к потери частных решений. Если уравнения
, может привести к потери частных решений. Если уравнения 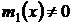 и
и 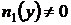 имеют вещественные решения
имеют вещественные решения 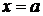 и
и 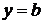 , то
, то 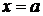 (при
(при 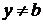 ) и
) и 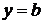 (при
(при 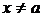 ) будут решениями уравнения (25). Эти решения, и только они, могут оказаться особыми, что проверяется дополнительным исследованием.
) будут решениями уравнения (25). Эти решения, и только они, могут оказаться особыми, что проверяется дополнительным исследованием.
Решение задачи Коши с начальными данными x0, y0 при условии 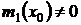 ,
, 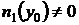 , а
, а 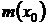 и
и 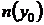 не равны нулю одновременно, можно получить из формулы (27), полагая С = 0. Если
не равны нулю одновременно, можно получить из формулы (27), полагая С = 0. Если 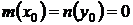 , то не гарантируется ни существование ни единственность решения.
, то не гарантируется ни существование ни единственность решения.
Единственность не нарушается когда начальная точка 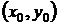 лежит на одном из частных решений вида
лежит на одном из частных решений вида 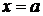 (
( 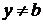 ),
), 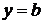 (
( 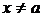 ).
).
Наконец, поле направлений в точке 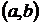 не определено, к этой точке примыкают решения
не определено, к этой точке примыкают решения 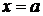 (
( 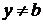 ),
), 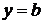 (
( 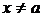 ).
).
Уравнение вида
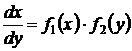 (28)
(28)
есть уравнение с разделяющимися переменными. Общий интеграл получается после разделения переменных квадратурой
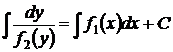 . (29)
. (29)
Если уравнение 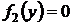 имеет вещественные решения вида
имеет вещественные решения вида 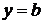 , то прямые
, то прямые 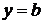 будут решениями уравнения (28). Эти решения могут оказаться особыми, других особых решений быть не может.
будут решениями уравнения (28). Эти решения могут оказаться особыми, других особых решений быть не может.
Уравнение с функцией специального вида
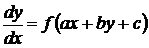 , (30)
, (30)
где a, b, c – постоянные, заменой переменных 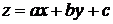 преобразуется в уравнение с разделяющимися переменными.
преобразуется в уравнение с разделяющимися переменными.
Примеры.
18. 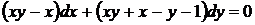 . Разлагая коэффициенты данного уравнения на множители, убеждаемся, что это уравнение с разделяющимися переменными (25)
. Разлагая коэффициенты данного уравнения на множители, убеждаемся, что это уравнение с разделяющимися переменными (25)
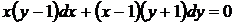 .
.
Разделяя переменные, запишем общий интеграл в форме (26)
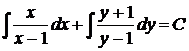
или
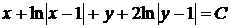 .
.
Подстановкой в исходное уравнение убеждаемся, что х = 1 и у = 1 являются частными решениями. Особых решений нет.
19. 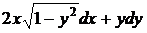 . Уравнение определено в полосе
. Уравнение определено в полосе 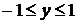 ,
, 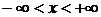 . Общий интеграл получаем после разделения переменных
. Общий интеграл получаем после разделения переменных
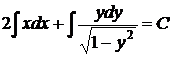 ,
, 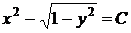 .
.
Подстановкой в исходное уравнение убеждаемся, что линии 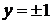 являются решениями этого уравнения, более того, они являются огибающими интегрального семейства кривых и потому особыми решениями.
являются решениями этого уравнения, более того, они являются огибающими интегрального семейства кривых и потому особыми решениями.
20. 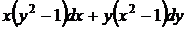 . Путем деления на произведение
. Путем деления на произведение 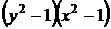 данное уравнение приводится к уравнению с разделенными переменными (22)
данное уравнение приводится к уравнению с разделенными переменными (22) 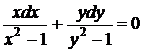 .
.
Используя формулу (23), сразу находим общий интеграл 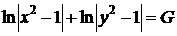
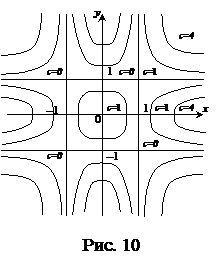 ,
,
который для удобства записи окончательного результата перепишем в виде
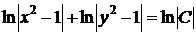 ,
,
или, потенцируя,
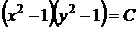 ,
, 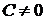 .
.
Общий вид семейства интегральных кривых показан на рис. 10. Прямые 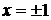 ,
, 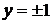 являются частными решениями данного уравнения, формально они не получаются из квадратуры, поскольку
являются частными решениями данного уравнения, формально они не получаются из квадратуры, поскольку 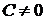 , но могут быть присоединены к общему интегралу уравнения (если положить
, но могут быть присоединены к общему интегралу уравнения (если положить 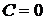 ).
).
Замечание. В геометрических вопросах и при нахождении общих интегралах выгоднее считать х и у равноправными и принимать за независимое переменное то х, то у (как удобнее). Наоборот, в исследованиях теоретико-функционального характера (доказательство существования решения или единственности решения начальной задачи) всегда надо рассматривать у как функцию от х; тогда, конечно, ранее упоминавшиеся (27) прямые 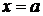 не являются решениями.
не являются решениями.
21. Найти решение 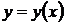 дифференциального уравнения
дифференциального уравнения
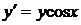 ,
,
удовлетворяющее начальному условию
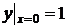 .
.
Нетрудно видеть, что функция 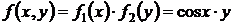 непрерывно по переменным х и у в любой области конечного диаметра, а значит всегда существует и при том единственное решение задачи Коши. Оно может быть найдено квадратурой (29) записанной в форме Коши, если положить
непрерывно по переменным х и у в любой области конечного диаметра, а значит всегда существует и при том единственное решение задачи Коши. Оно может быть найдено квадратурой (29) записанной в форме Коши, если положить 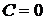
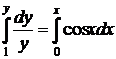 ,
, 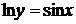 ,
, 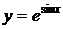 .
.
Если в качестве начального условия взять 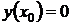 , то получится единственное тривиальное (вырожденное) решение
, то получится единственное тривиальное (вырожденное) решение 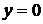 .
.
22. 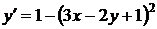 . Это уравнение вида (30).
. Это уравнение вида (30).
Положим 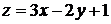 . Тогда
. Тогда 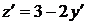 . Используя исходное уравнение, имеем
. Используя исходное уравнение, имеем
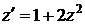 , разделяя переменные
, разделяя переменные 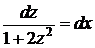 ,
,
квадратурой 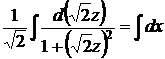 находим общий интеграл
находим общий интеграл
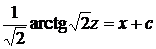 или
или 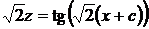 ,
,
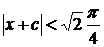 . Возвращаясь к старым переменным и преобразуя, находим общее решение
. Возвращаясь к старым переменным и преобразуя, находим общее решение 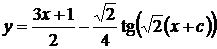 .
.
Однородное уравнение
Функция  однородной степени m относительно х и у, если при любом t справедливо равенство
однородной степени m относительно х и у, если при любом t справедливо равенство
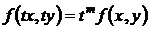 , (31)
, (31)
где t – произвольное число, m – степень однородности (измерение).
Полагая в формуле (31) 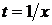 , найдем представление для однородной степени т функции
, найдем представление для однородной степени т функции
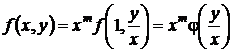 . (32)
. (32)
Дифференциальное уравнение
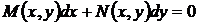 (7)
(7)
называется однородным, если 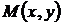 и
и 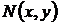 – однородные функции своих аргументов одинаковой степени однородности, непрерывные вместе со своими частными производными первого порядка; его легко записать в виде
– однородные функции своих аргументов одинаковой степени однородности, непрерывные вместе со своими частными производными первого порядка; его легко записать в виде
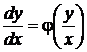 ,
, 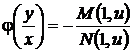 . (33)
. (33)
Однородное уравнение приводится к уравнению с разделяющимися переменными подстановкой
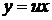 ,
, 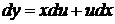 . (34)
. (34)
В самом деле, подставляя (34) в (33), получаем
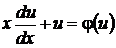 , или
, или 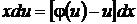 . (35)
. (35)
Это уравнение с разделяющимися переменными (25). Разделяя в нем переменные, квадратурой найдем общий интеграл
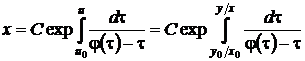 ,
, 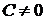 , (36)
, (36)
где 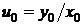 выбрано произвольно, но так, чтобы интеграл существовал, С – произвольная постоянная. Из формулы (36) умножением на и (обеих частей левого равенства) получаем параметрическое представление интегральной кривой с параметром и
выбрано произвольно, но так, чтобы интеграл существовал, С – произвольная постоянная. Из формулы (36) умножением на и (обеих частей левого равенства) получаем параметрическое представление интегральной кривой с параметром и
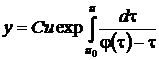 . (37)
. (37)
Из правого равенства (36) видно, что семейство интегральных кривых представляется общим уравнением
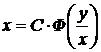 ,
, 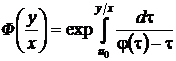 ,
,
где С – произвольная постоянная. Все кривые подобны между собой с центром подобия в начале координат, меняется лишь отношение подобия. В этом можно убедиться заменой 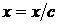 и
и 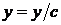 в уравнении
в уравнении
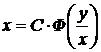 .
.
Обратно, если дано какое-нибудь семейство кривых, подобных относительно начала координат, то соответствующее дифференциальное уравнение будет однородным уравнением первого порядка. Начало координат 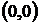 всегда является особой точкой для однородного уравнения (подробно этот вопрос рассмотрен), поэтому изоклинами
всегда является особой точкой для однородного уравнения (подробно этот вопрос рассмотрен), поэтому изоклинами 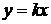
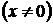 однородного уравнения являются полупрямые, выходящие из начала координат и лежащие в области задания уравнения. Все интегральные кривые, пересекающие такую полупрямую, образуют с ней один и тот же угол. Если k удовлетворяет условию
однородного уравнения являются полупрямые, выходящие из начала координат и лежащие в области задания уравнения. Все интегральные кривые, пересекающие такую полупрямую, образуют с ней один и тот же угол. Если k удовлетворяет условию 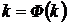 , то изоклина
, то изоклина 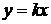
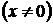 будет интегральной кривой.
будет интегральной кривой.
Дифференцируя по параметру и выражения (36), (37)
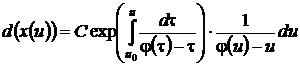 ,
,
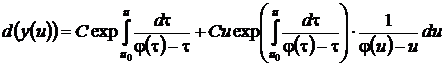 ,
,
непосредственно убеждаемся в том, что при 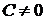 они действительно являются решениями уравнения (33) с однородной функцией
они действительно являются решениями уравнения (33) с однородной функцией 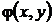 нулевой степени однородности
нулевой степени однородности
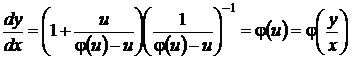 .
.
Заметим, что решение 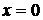 уравнения (35) получается из формулы (36) при
уравнения (35) получается из формулы (36) при 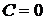 , но оно не всегда является решением уравнения (33). Например, при
, но оно не всегда является решением уравнения (33). Например, при 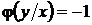 полупрямая
полупрямая 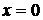 не является решением уравнения (33), поскольку не удовлетворяет перевернутому уравнению
не является решением уравнения (33), поскольку не удовлетворяет перевернутому уравнению 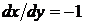 ; если
; если 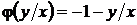 , то
, то 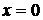 удовлетворяет уравнению
удовлетворяет уравнению
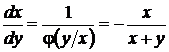
и поэтому является решением уравнения (33). Вообще говоря, для уравнения (33) общий интеграл (36) становится неопределенным при 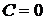 .
.
Если 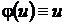 , то с учетом подстановки (34) уравнение (33) принимает вид
, то с учетом подстановки (34) уравнение (33) принимает вид 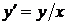 ; его общее решение
; его общее решение  . С другой стороны, в процессе получения формул (36), (37) могли быть потеряны решения, определяемые равенством
. С другой стороны, в процессе получения формул (36), (37) могли быть потеряны решения, определяемые равенством 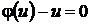 , которое можно записать в виде уравнения
, которое можно записать в виде уравнения
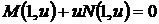 .
.
Пусть 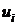
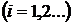 – вещественные корни такого уравнения. Тогда полупрямые
– вещественные корни такого уравнения. Тогда полупрямые 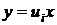
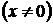 будут решениями однородного уравнения (33) и среди них (включая полуоси ОУ
будут решениями однородного уравнения (33) и среди них (включая полуоси ОУ 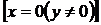 ) могут быть особые решения (полный анализ особых решений уравнения (33) показан). Однородное уравнение (7) заведомо не имеет особых решений, если функции
) могут быть особые решения (полный анализ особых решений уравнения (33) показан). Однородное уравнение (7) заведомо не имеет особых решений, если функции 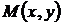 и
и 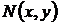 являются однородными полиномами, иначе, формами от х и у. Вообще, для функций
являются однородными полиномами, иначе, формами от х и у. Вообще, для функций 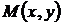 и
и 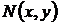 непрерывных вместе со своими частными производными первого порядка в некоторой области G можно не проводить исследования на любые решения уравнения (7) в этой области. Особые решения могут быть лишь на границе
непрерывных вместе со своими частными производными первого порядка в некоторой области G можно не проводить исследования на любые решения уравнения (7) в этой области. Особые решения могут быть лишь на границе 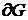 этой области.
этой области.
При фактическом интегрировании однородного дифференциального уравнения необязательно приводить его к виду (33); достаточно убедиться в том, что уравнение принадлежит к рассматриваемому типу, и непосредственно применить подстановку (34); пользоваться готовыми формулами (36), (37) тоже не всегда целесообразно.
Уравнения, приводящиеся к однородному.
А. Рассмотрим уравнение вида
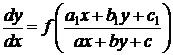 (38)
(38)
Если
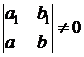 , (39)
, (39)
то это дифференциальное уравнение при помощи подстановки
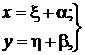 (40)
(40)
где 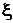 и
и 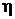 – новые переменные, а
– новые переменные, а 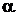 и
и 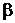 – постоянные числа, определяемые из системы
– постоянные числа, определяемые из системы
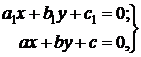
приводится к однородному уравнению
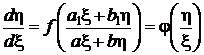 .
.
Если
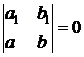 , (41)
, (41)
то уравнение (38) принимает ранее рассмотренный вид
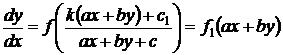 . (30)
. (30)
уравнения с функцией специального вида (30).
В. Рассмотрим еще уравнение
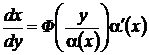 , (42)
, (42)
где 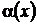 – непрерывная вместе со своей производной функция. Заменой
– непрерывная вместе со своей производной функция. Заменой 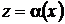 ,
, 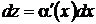 это уравнение приводится к однородному дифференциальному уравнению.
это уравнение приводится к однородному дифференциальному уравнению.
С. Иногда дифференциальное уравнение можно привести к однородному заменой переменного 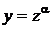 (α – постоянное). Это возможно в том случае, когда в уравнении все члены оказываются одинаковой степени однородности, если переменной х приписать степень однородности 1, переменной у – α и производной
(α – постоянное). Это возможно в том случае, когда в уравнении все члены оказываются одинаковой степени однородности, если переменной х приписать степень однородности 1, переменной у – α и производной 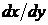 – соответственно α – 1.
– соответственно α – 1.
Примеры.
23. Показать, что дифференциальное уравнение семейства кривых, подобных и подобно расположенных по отношению к началу координат, если уравнение однородное.
Уравнение семейства имеет вид
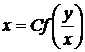 , отсюда
, отсюда 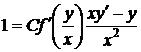 .
.
Исключая С, получим однородное уравнение
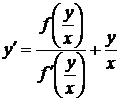 или, переобозначая,
или, переобозначая, 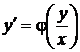 .
.
Оно допускает группу преобразований 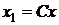 ,
, 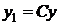 , так как
, так как 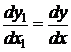 и
и 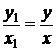 .
.
Это – преобразованная подобия (гомотетия) с центром подобия в начале координат; все направления касательных поля (направлений) одинаковы на каждой полупрямой, проходящей через начало; эти полупрямые являются изоклинами.
24. Проинтегрировать уравнение 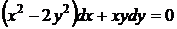 .
.
Здесь коэффициенты уравнения, согласно формуле (31)
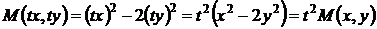 ,
,
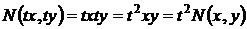 ,
,
являются однородными функциями одной и той же степени т = 2 (квадратичными формами), поэтому уравнение однородное.
Производя замену (34) 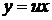 ,
, 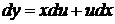 ,
,
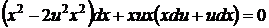 ,
,
сокращая на х2 (х ≠0) и преобразуя, приходим к уравнению
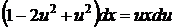 , или
, или 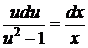 .
.
Квадратурой получаем
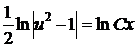 , или
, или 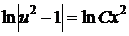 .
.
Отсюда
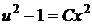 , обратная замена,
, обратная замена, 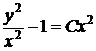 ,
,
окончательно, 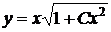 .
.
25. Для уравнения 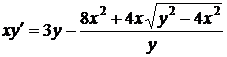 найти интегральные кривые, проходящие через точки: а) (1,3); б) (1,2).
найти интегральные кривые, проходящие через точки: а) (1,3); б) (1,2).
Прежде всего заметим, что данное уравнение однородное
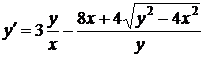 ,
, 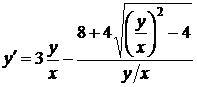 .
.
Оно задано в той части плоскости, где выполняется условие
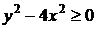 , или
, или 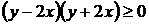
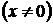 ;
;
показано штриховкой на рис. 11.
Применяя подстановку 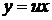 ,
, 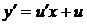 и преобразуя
и преобразуя
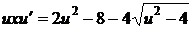 ,
, 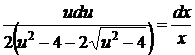 ,
,
 квадратурой
квадратурой
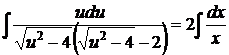 ,
,
находим общий интеграл промежуточного уравнения
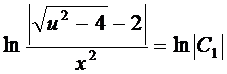 ,
, 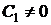 ,
,
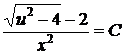
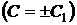 .
.
Обратной заменой, находим общее решение
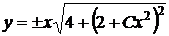 ,
, 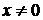
заданного дифференциального уравнения.
При преобразованиях могли быть потеряны решения. Из уравнения
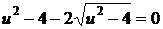
находим 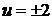 ,
, 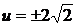 . Это дает решения заданного уравнения
. Это дает решения заданного уравнения 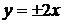 – особые,
– особые, 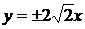 – частные (они могут быть получены из общего, если положить С = 0).
– частные (они могут быть получены из общего, если положить С = 0).
Обратимся теперь к поставленным задачам Коши.
а) Полагая в общем решении х = 1, у = 3, находим 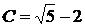 , так что искомым решением будет кривая
, так что искомым решением будет кривая
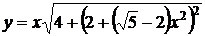
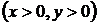 .
.
б) Точка (1,2) особая, поскольку она лежит на особом решении (на границе области задания) 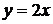 (х > 0). Следовательно, в этой точке нарушается единственность решения задачи Коши. В самом деле, полагая х = 1, у = 2, находим С = –2, значит в точке (1,2) примыкает решение частное
(х > 0). Следовательно, в этой точке нарушается единственность решения задачи Коши. В самом деле, полагая х = 1, у = 2, находим С = –2, значит в точке (1,2) примыкает решение частное
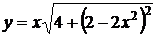 ,
,
а с другой стороны через эту же точку (1,2) проходит особое решение 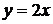
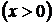 .
.
Точка (0,0) – особая точка данного уравнения, к ней примыкают все интегральные кривые; ось ОУ не является решением (рис. 11).
26. 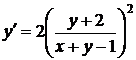 . Это дифференциальное уравнение вида (38) в случае, когда выполняется условие (39). В этом случае уравнения преобразуются в однородные путем переноса начала координат в точку пересечения
. Это дифференциальное уравнение вида (38) в случае, когда выполняется условие (39). В этом случае уравнения преобразуются в однородные путем переноса начала координат в точку пересечения 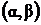 прямых
прямых
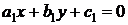 и
и 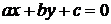 ,
,
так как в новых координатах 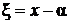 ,
, 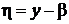 свободный член в уравнениях этих прямых будет равен нулю.
свободный член в уравнениях этих прямых будет равен нулю.
В данном примере α = 3, β = –2, а подстановка (40)
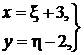 или
или 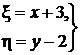
приводит уравнение к однородному, которое далее решается с помощью стандартной замены 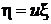 ,
, 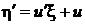 .
.
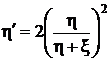 ,
, 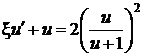 ,
, 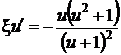 .
.
Разделяя переменные, разделяя на элементарные дроби,
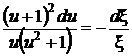 ,
, 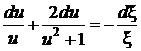 ,
,
квадратурой
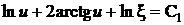 ,
,
возвращаясь к первоначальным переменным, находим общий интеграл заданного уравнения
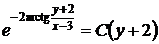 ,
, 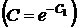 .
.
27. 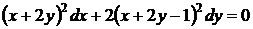 . Это дифференциальное уравнение приводится к виду (38), когда выполняется условие (41). В этом случае замена переменных
. Это дифференциальное уравнение приводится к виду (38), когда выполняется условие (41). В этом случае замена переменных 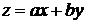 преобразует рассматриваемые уравнения в уравнения с разделяющимися переменными.
преобразует рассматриваемые уравнения в уравнения с разделяющимися переменными.
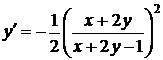 ; замена
; замена 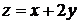 ,
, 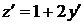
приводит уравнение к виду
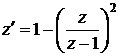 ,
, 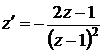 или
или 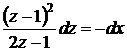 .
.
Элементарно преобразуя
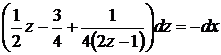
и интегрируя, имеем
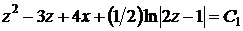 ,
,
или, возвращаясь к старым переменным, общий интеграл исходного уравнения в свободном от ограничений виде
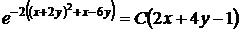 ,
, 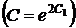 .
.
28. 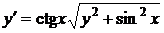 . Это уравнение вида (42), оно станет однородным, если сделать замену независимой переменной
. Это уравнение вида (42), оно станет однородным, если сделать замену независимой переменной 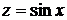 ,
, 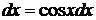
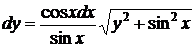 ,
, 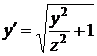 .
.
Стандартной заменой 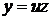 ,
, 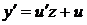 и преобразованием с использованием сопряженного выражения, приводим последнее уравнение к виду, удобному для интегрирования
и преобразованием с использованием сопряженного выражения, приводим последнее уравнение к виду, удобному для интегрирования
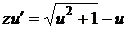 ,
, 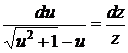 , или
, или 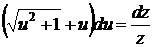 .
.
С использованием формулы
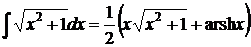 ,
,
квадратурой находим общий интеграл
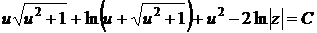
промежуточного уравнения, или, возвращаясь к старым переменным и преобразуя, общий интеграл данного уравнения
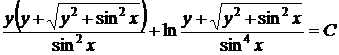 .
.
29. 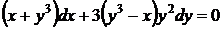 . Это частный случай уравнения (42).
. Это частный случай уравнения (42).
Делаем подстановку 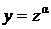 ,
, 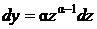 , где α пока произвольное число, которое выберем позже. Подставляя выражения для у и dy в исходное уравнение, получим
, где α пока произвольное число, которое выберем позже. Подставляя выражения для у и dy в исходное уравнение, получим
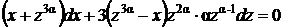 ,
,
или 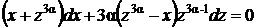 .
.
Отсюда видно, что если положить 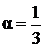 , то уравнение станет однородным, поскольку его коэффициенты станут линейными формами (многочленами первой степени однородности).
, то уравнение станет однородным, поскольку его коэффициенты станут линейными формами (многочленами первой степени однородности).
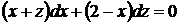 , или
, или 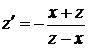 .
.
Далее, стандартной заменой 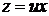 ,
, 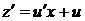 , приводим уравнение к виду
, приводим уравнение к виду
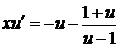 , или
, или 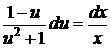 ,
,
выполняя квадратуру, получаем общий интеграл
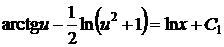 ,
,
который в первоначальных переменных выглядит так
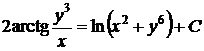 ,
, 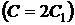 .
.
