Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, существование промежуточных значений.

Определение 8. Функции 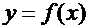называется непрерывной на сегменте (отрезке) 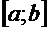, если она непрерывна во всех внутренних точках этого сегмента, непрерывна справа в точке 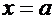и непрерывна слева в точке 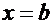.Теорема 4. (Вейерштрасса) Если функция 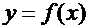непрерывна на сегменте 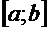, то она ограничена и достигает своего наибольшего и наименьшего значения.Теорема 5. (Больцано-Коши) Если функция 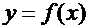непрерывна на сегменте 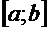и на его концах принимает значения разных знаков, то внутри этого сегмента найдется, по крайней мере, одна точка 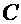, в которой функция равна нулю.Геометрический смысл теоремы заключается в следующем: если точки графика функции 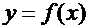, соответствующие концам сегмента 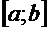, лежат по разные стороны от оси OX, то этот график хотя бы в одной точке сегмента пересекает ось OX.Теорема 6. 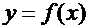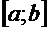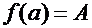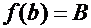(О промежуточном значении функции) Если функция непрерывна на сегменте и , , то для любого 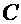, заключенного между 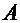и 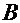, найдется внутри сегмента такая точка 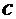, что 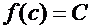. Теорема 7. (О существовании обратной функции) Если функция 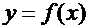непрерывна на сегменте 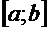и возрастает (убывает) на этом сегменте, то обратная функция 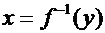на соответствующем сегменте оси OY существует и является также возрастающей (убывающей) функцией.

Производная функции, ее геометрический и физический смысл. Связь между непрерывностью и дифференцируемостью функции.

Определение 1. Число 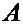называется производной функции 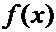в точке 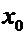, если существует предел 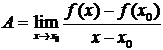(т.е. производной функции 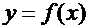в точке называется предел отношения приращения функции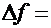 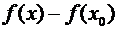в точке 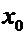к вызвавшему его приращению аргумента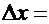 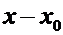при условии, что : ).

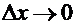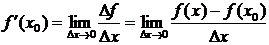Производная обозначается как 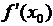или как .

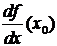Определение 2. Касательной к графику функции 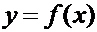в точке 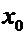называют предельное положение секущей при .

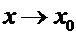Так как 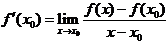,то уравнение касательной имеет вид

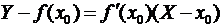Геометрический смысл производной состоит в том, что она является угловым коэффициентом касательной к графику функции 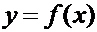в точке 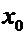.Определение 3. Если функция 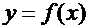имеет производную в некоторой точке, то она называется дифференцируемой в этой точке. Процесс нахождения производной называется дифференцированием функции.Определение 4. Функция 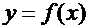называется дифференцируемой в интервале (a;b), если она дифференцируема в каждой точке этого интервала. Теорема 1. Если функция 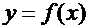дифференцируема в некоторой точке, то она в этой точке непрерывна.

Правила нахождения производной: производная произведения и производная частного.

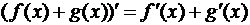
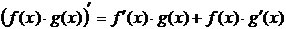
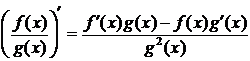
31. Производная сложной и обратной функции.Теорема 6. Если функция 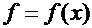имеет производную 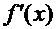в точке 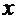, а функция 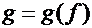имеет производную 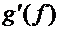в соответствующей точке 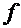, то сложная функция 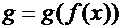в данной точке имеет производную 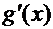, которая находится по формуле 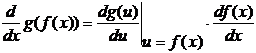или

.

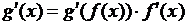Теорема 5. Пусть функция 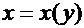монотонна в некотором интервале 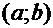и имеет в некоторой точке 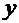этого интервала производную 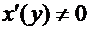. Тогда в соответствующей точке 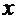обратная функция 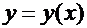имеет производную 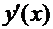, причем

.
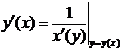