Неполные уравнения плоскости.

Если хотя бы одно из чисел А, В, С, D равно нулю, уравнение (8.2) называют неполным.

Рассмотрим возможные виды неполных уравнений:

1) D = 0 — плоскость Ax + By + Cz = 0 проходит через начало координат.

2) А = 0 — n = {0,B,C}Ox, следовательно, плоскость By + Cz + D = 0 параллельна оси Ох.

3) В = 0 — плоскость Ax + Cz +D = 0 параллельна оси Оу.

4) С = 0 — плоскость Ax + By + D = 0 параллельна оси Оz.

5) А = В = 0 — плоскость Cz + D = 0 параллельна координатной плоскости Оху (так как она параллельна осям Ох иОу).

6) А = С = 0 — плоскость Ву + D = 0 параллельна координатной плоскости Охz.

7) B = C = 0 — плоскость Ax + D = 0 параллельна координатной плоскости Оуz.

8) А = D = 0 — плоскость By + Cz = 0 проходит через ось Ох.

9) B = D = 0 — плоскость Ах + Сz = 0 проходит через ось Оу.

10) C = D = 0 - плоскость Ax + By = 0 проходит через ось Oz.

11) A = B = D = 0 — уравнение Сz = 0 задает координатную плоскость Оху.

12) A = C = D = 0 — получаем Ву = 0 — уравнение координатной плоскости Охz.

13) B = C = D = 0 — плоскость Ах = 0 является координатной плоскостью Оуz.

Если же общее уравнение плоскости является полным ( то есть ни один из коэффициентов не равен нулю), его можно привести к виду: (8.3) называемому уравнением плоскости в отрезках. Способ преобразования показан в лекции 7. Параметры а, b и сравны величинам отрезков, отсекаемых плоскостью на координатных осях.

Всякая плоскость в пространстве, снабженном декартовой системой координат, есть множество вех точек, удовлетворяющих некоторому линейному уравнению вида: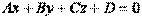

Всякую плоскость в пространстве можно задать, указав какую – ни будь ее точку и два произвольных приложенных к этой точке неколлинеарных вектора: 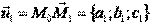и .

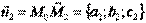-векторноеур-е плоскости.

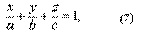
(7)- Уравнение (7) называют уравнением плоскости в отрезках на осях, т.к. числа a, b, c имеют простой геометрический смысл: а - абсцисса точки пересечения плоскости с осью Ох, b - ордината точки пересечения плоскости с осью Оу, с - аппликата точки пересечения плоскости с осью Oz.

-параметрическое уравнение прямой :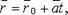

где 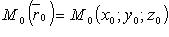- фиксированная точка, лежащая на прямой; 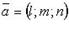-направляющий вектор.

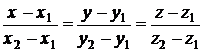- это называют уравнениями прямой, проходящей через две заданные точк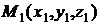и и .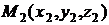

Прямая в пространстве может быть задана:

1) как линия пересечения двух плоскостей,т.е. системой уравнений:

A₁ x + B₁ y + C₁ z + D₁ = 0, A₂ x + B₂ y + C₂ z + D₂ = 0;

2) двумя своими точками M₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂), тогда прямая, через них проходящая, задается уравнениями:

=

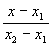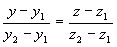
3) точкой M₁(x₁, y₁, z₁), ей принадлежащей, и вектором a(m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:

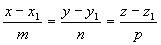
ВИДЫ УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ:

Уравнение прямой с угловым коэффициентом:y= kx + b

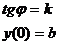
Уравнение прямой в отрезках: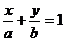

Общее уравнение прямой: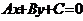

Уравнение с данным направляющим вектором и проходящей через данную точку:

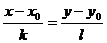
Уравнение прямой с данным вектором нормали

и проходящей через данную точку: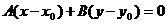

ВОПРОС 23-24. Плоские кривые второго порядка (эллипс, гипербола, парабола). Канонические уравнения кривых второго порядка.

Плоские кривые.
Все множество плоских кривых можно разделить на циркульные и лекальные.
Циркульнойназыв. кривую, кот.можно построить с помощью циркуля. Это окружность, овал, завиток.

Эллипс - кривая второго порядка, сумма расстояний от любой точки которой до двух фиксированных точек, называемых фокусами, есть величина постоянная, равная большой оси эллипса.

Парабола - кривая второго порядка, расстояние от любой точки которой до фокуса равно расстоянию от этой точки до некоторой фиксированной прямой, называемой директрисой.

Гипербола - кривая второго порядка, разность расстояний от любой точки которой до двух фокусов есть величина постоянная, равная действительной оси гиперболы. Вдоль действительной оси расположены ветви гиперболы.

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида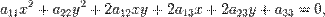

в котором по крайней мере один из коэффициентов 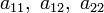отличен от нуля.

Каноническое уравнение любой невырожденной кривой второго порядка при помощи подходящего преобразования начала координат может быть приведено к виду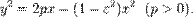

Уравнение выражает тот факт, что невырожденная кривая второго порядка является геометрическим местом точек, отношение расстояний которых 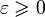от данной точки (фокуса) и от данной прямой (директрисы) постоянно. Кроме того, при 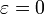кривая является окружностью, при 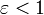— эллипсом, при 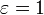— параболой, при 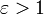— гиперболой.

Уравнение директрисы кривой выражается уравнением 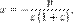а координаты фокуса 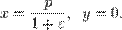Директриса перпендикулярна оси симметрии, проходящей через фокус и вершину кривой (фокальная ось). Расстояние между фокусом и директрисой равно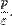

Вопрос 25. Последовательности. Определение, способы задания, действия с последовательностями.

Определение. Если по некоторому закону каждому натуральному числу 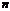поставлено в соответствие вполне определенное число 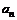, то говорят, что задана числовая последовательность : .

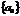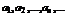Числа 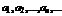называются членами последовательности, а число 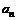- общим или 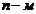членом последовательности.

Примеры числовых последовательностей:

- 2, 4, 6, 8, …, 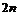, … (монотонная неограниченная),

- 1, 0, 1, 0, … (не монотонная, ограниченная).

Закон образования последовательности дается формулой его общего члена (одной или несколькими). Последовательность может быть сформирована также с помощью рекуррентного соотношения или словесного описания общего члена.

Пример. Дана формула общего элемента последовательности 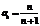. Написать пять первых элементов последовательности.

Полагая последовательно 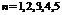в общем элементе 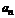получаем , , , , .

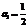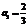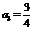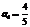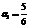Действия с последовательностями:

-сложение –вычитание –умножение -деление