Промежутки знакопостоянства функции.

Аналитический способ.

Аналитический способ - это наиболее часто встречающийся способ задания функции.

Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у.

Графический способ.

При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом .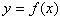

Словесный способ.

Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.

«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».

Табличный способ.

Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.

Типы ф-й

Сложная

Сложная функция - это функция от функции

Неявная

Неявные функции - это функции, заданные уравнением, не разрешенным относительно зависимой переменной.

Обратная

Если уравнение y=f(x) может быть однозначно разрешено относительного переменного x (т.е. сущ. Ф-я x=g(y) такая, что y=f[g(y)]), то ф-я x=g(y) – обратная по отношению к y=f(x).

Основные свойства функций.

1) Область определения функции и область значений функции.

Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.

Область значений функции - это множество всех действительных значений y, которые принимает функция.

Нули функции.

Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

Промежутки знакопостоянства функции.

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

Монотонность функции.

Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Четность (нечетность) функции.

Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.

Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.

Ограниченная и неограниченная функции.

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.

Периодическость функции.

Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

Предел ф-ии

Предел ф-ии (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.

Последовательность an называется бесконечно малой, если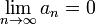

Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Последовательность an называется бесконечно большой, если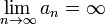

Первый замечательный предел

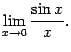
Второй замечательный предел

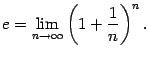
Непрерывность ф-ии

Ф-яf(x) называется непрерывной при x = E, если

1) Эта ф-я определена в точке E, т.е. существует число f(E)

2) Существует конечный предел limf(x)

3) Этот предел равен значению ф-ии в точкеE, т.е. x -> E.

Точки разрыва

Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.

Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

Производная сложной функции

Рассмотрим сложную функцию y = y(u(x))

Теорема 4. Если функции y = y(u), u = u(x) дифференцируемы (т.е. существуют производные y'_u, u'_x), тогда сложная функция y = y(u(x)) дифференцируема и y'_x = y'_u u'_x.

Доказательство

Если аргумент x получит приращение Δx, то функция u получит приращение Δu = u(x + Δx) − u(x), а функция y получит приращение Δy = y(u + Δu) − y(u). Но тогда, воспользовавшись свойствами предела функции, получаем

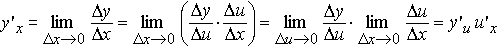
Теорема доказана.

Доказательство

Если аргумент x получит приращение Δx, то функция f получит приращение Δy = f(x + Δx) − f(x). С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом:Δx=g(y + Δy) − g(y).

Тогда получаем

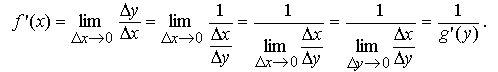
Теорема доказана.

Производные высших порядков

Дифференцируемость функции

Функция y=f(x)называется дифференцируемой в некоторой точке x₀, если она имеет в этой точке определенную производную, т.е. если предел отношения 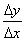существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что онадифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Правило Лопиталя

Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть 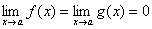или 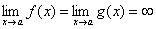. Тогда, если существует предел отношения производных этих функций 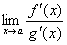, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

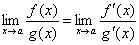(1)

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.

Например, найти 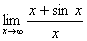. Этот предел существует 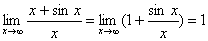. Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.

Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.

Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.

Для раскрытия неопределенностей 1∞, 10, ∞0 нужно прологарифмировать данную функцию и найти предел ее логарифма.

Монотонность ф-ии

Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Экстремумы

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.

Первое достаточное условие.

Пусть xо - критическая точка. Если f ' (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную

f ' (x) в окрестности точки xо и вторую производную f"(xo) в самой точке xо. Если f '(xо) = 0, f"(xo)>0 (f"(xo)<0), то точка xо является точкой локального минимума (максимума) функции f(x). Если же f"(xo)=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

Точки перегиба

Точка графика непрерывной функции, отделяющая его выпуклую часть отвогнутой, называется точкой перегиба.

Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.

Определим достаточные условия того, что данная точка кривой является точкой перегиба.

Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значениеx = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба.

Доказательство. Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0.

Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.

Асимптоты графика функции

Прямая называется асимптотой графика функции y = f(x), если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте.

Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.

Формула Тейлора

Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.

ФОРМУЛА ТЕЙЛОРА

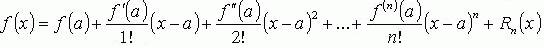
, где R_n(x) - остаточный член формулы Тейлора.

Аналитический способ.

Аналитический способ - это наиболее часто встречающийся способ задания функции.

Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у.

Графический способ.

При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом .

Словесный способ.

Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.

«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».

Табличный способ.

Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.

Типы ф-й

Сложная

Сложная функция - это функция от функции

Неявная

Неявные функции - это функции, заданные уравнением, не разрешенным относительно зависимой переменной.

Обратная

Если уравнение y=f(x) может быть однозначно разрешено относительного переменного x (т.е. сущ. Ф-я x=g(y) такая, что y=f[g(y)]), то ф-я x=g(y) – обратная по отношению к y=f(x).

Основные свойства функций.

1) Область определения функции и область значений функции.

Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.

Область значений функции - это множество всех действительных значений y, которые принимает функция.

Нули функции.

Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

Промежутки знакопостоянства функции.

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

Монотонность функции.

Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.