Глава 12. Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых

В декартовых координатах каждая прямая определяется уравнением первой степени и, обратно, каждое уравнение первой степени определяет прямую.

Уравнение вида

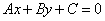(1)

называется общим уравнением прямой.

Угол 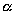, определяемый, как показано на рис., называется углом наклона прямой к оси Ох. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой; его обычно обозначают буквой k:

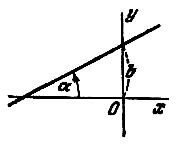
Уравнение 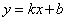называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент, b - величина отрезка, который отсекает прямая на оси Оу, считая от начала координат.

Если прямая задана общим уравнением

,

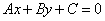то ее угловой коэффициент определяется по формуле

.

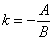Уравнение 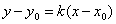является уравнением прямой, которая проходит через точку 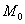( 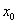, 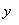) и имеет угловой коэффициент k.

Если прямая проходит через точки 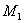( 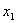, 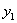), 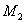( 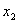, 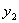), то ее угловой коэффициент определяется по формуле

.

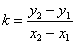Уравнение

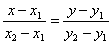
является уравнением прямой, проходящей через две точк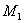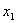и ( , ) и ( , ).

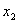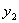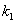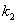Если известны угловые коэффициенты и двух прямых, то один из углов 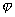между этими прямыми определяется по формуле

.

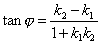Признаком параллельности двух прямых является равенство их угловых коэффициентов:

.

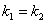Признаком перпендикулярности двух прямых является соотношение

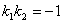, или .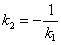

Иначе говоря, угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку.

Признаки параллельности прямых (формулировки и примеры).

I. Две прямые, параллельные третьей* параллельны.

II. Если внутренние накрест лежащие углы равны, то прямые параллельны

III. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны.

IV. Если соответственные углы равны, то прямые параллельны.

Перпендиуклярность

Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.

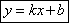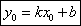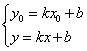
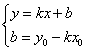
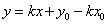
Уравнение прямой, проходящей через точку, в данном направлении.т М (х₀;у₀).Уравнение прямой записывается в виде .Подставим в это уравнение точку М Решим систему: 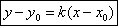Уравнение прямой, проходящей через 2 точки.К (х₁;у₁) М (х₂;у₂)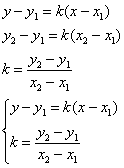 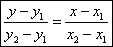Уравнение прямой в отрезках.К (а;0); М (0;b)Подставим точки в уравнение прямой: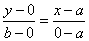 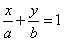Уравнение прямой, проходящей через данную точку, перпендикулярно данномувектору.М₀ (х₀;у₀). 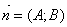Возьмем произвольную точку М (х;у). 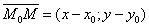Т.к. 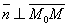, то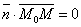

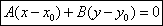
Вопрос №8

Эллипс-множество точек плоскости, сумма расстояния от которых до двух данных точек в плоскости, называемых фокусами есть величина постоянная.

Точки пересечние эллипса с осями координат называются вершинами эллипса. Из симметрии эллипса следует что кроме вершин А(а,0) и Б(0,б) эллипс имеет еще 2 вершины А1(-а,0) и Б1(0,-б) отрезки А А1 и Б Б1 соденяющие противоположные врешины эллипса а также их длины 2 а и 2 б называются называеются соотвественно большой и малой осями эллипса. Числа а и б называет большой и малой полуосями элиипса.

Отношении фокального расстояния к длине большой оси называется экцентриситетом эллипса и обозначает эпсилон.

Гипербола-множество всех точек плоскости, абсолютная величина разности расстояний каждой из которых до двух данных точек этой плоскости, называемых фокусами есть величина постоянная.

Отношение фокального расстояния к длине действительной оси называется экцентриситетом пораболы. Действительной осью называет отрезок 2а, который соеденияет вершины гиперболы. Числа а и б называются действительной и мнимой полуюсями гиперболы.

Парабола-множество всех точек плоскости равноудаленных от данной точки F, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса до директрисы называется параметром параболы.

Эксцентриситет: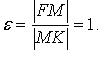

Отношение фокального радиуса к хз чемуJ

Вывод кононического уравнения:

Эллипс x^2/a^2+y^2/b^2=1

Гипербола x^2/a^2-Y^2/b^2=1

Парабола y^2=px p-директриса

Выводы на листке.

Вопрос №9

Пересечение 2ух не компланарных плоскостей образуют прямую в пространстве.

Прямая в пространстве вполне определяется заданием фиксированной точки м и направляющим веткором