Интегралы с бесконечными пределами.

Пусть функция 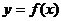непрерывна при любом 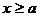. Рассмотрим определённый интеграл с переменным верхним пределом

.

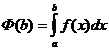Предположим, что при 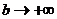функция 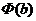имеет конечный предел; этот предел называется сходящимся несобственным интеграломот функции 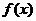по промежутку 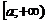и обозначается

.

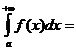
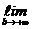
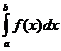Если же этот предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся.

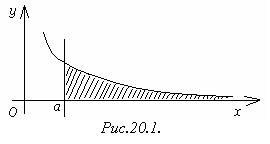
Геометрически несобственный интеграл от неотрицательной функции выражает площадь бесконечной криволинейной трапеции, ограниченной сверху графиком функции 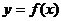, слева - прямой 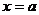, снизу - осью (В случае сходящегося интеграла эта площадь является конечной, в случае расходящегося - бесконечной) (Рис.20.1.).

Если 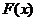- первообразная для 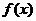, то

= =

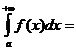
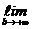
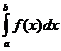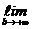
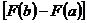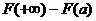= , где = .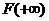

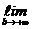
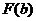и несобственный интеграл с обоими бесконечными пределам

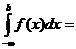
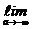
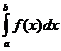и несобственный интеграл с обоими бесконечными пределами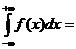 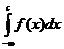+ 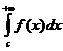, где с - любая точка из интервала .

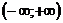С помощью следующих двух теорем можно исследовать вопрос о сходимости некоторых несобственных интегралов.

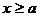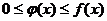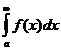Теорема 1.Если при выполнены неравенства и сходится, то сходится и 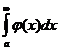, причём

£ ;

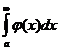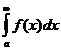если же 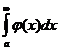расходится, то расходится и интеграл .

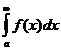Теорема 2. Если в промежутке 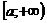функция 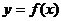меняет знак и 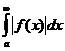сходится, то сходится также .

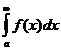Интегралы от неограниченных функций.

Если функция 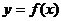не ограничена в окрестности точки с отрезка 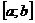и непрерывна пр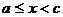и и 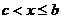, то несобственный интеграл от этой функции определяется формулой

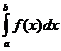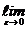
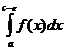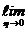
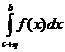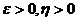= + , где (1)

В случае, когда 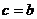или 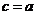, получаем

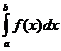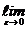
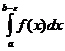= (2)

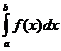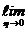
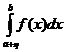= (3)

Несобственный интеграл (2) или (3) называется сходящимся, если существует конечный предел соответствующего определённого интеграла; в противном случае интеграл называется расходящимся. Несобственный интеграл (1) называется сходящимся, если существует и конечны оба предела в правой части.

Для интегралов от неограниченных функций справедливы теоремы, аналогичные теоремам 1 и 2.

Основные понятия.

Определение. Пусть имеется n переменных величин, и каждому набору их значений ( 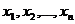) из некоторого множества X соответствует одно вполне определённое значение переменной величины z. Тогда говорят, что задана функция нескольких переменных z = ( ).

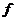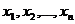Пример.Формула V = 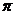R²H задаёт объём цилиндра V как функцию двух переменных V(R;H), где R − радиус основания, H − высота цилиндра.

Переменные 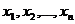называются независимыми переменными или аргументами, z зависимой переменной,а символ 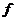означает закон соответствия. Множество X называется область определения функции.

Рассмотрим некоторые примеры функции нескольких переменных:

1. Функция z = 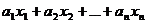, где 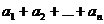, 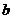− постоянные числа, называется линейной.

2. Функция z = 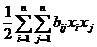, где 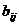− постоянные числа, называется квадратической.

3. Одно из базовых понятий экономической теории − функция полезности.Эта функция z = 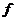( 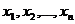), выражающая полезность от n приобретённых товаров 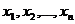. Чаще всего встречаются следующие её виды:

а) z = 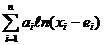, где 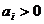, , 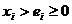− логарифмическая функция;

б) z = 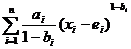, где 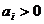, , 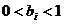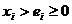− функция

Постоянной эластичности.

4. Также часто в экономике встречается понятие производственной функции, выражающей результат производственной деятельности от обусловивших его факторов. Например, при n = 2 для величины общественного продукта z = 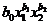, где 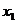− затраты труда, 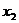− объём производственных фондов, 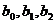− постоянные числа.

В дальнейшем будем вести изложение для функции двух переменных (n= 2). При этом, практически все понятия и теоремы, сформулированные для n =2, легко переносятся и на случай n > 2 кроме того, рассмотрения двух переменных позволяет использовать наглядную иллюстрацию.

Предел и непрерывность.

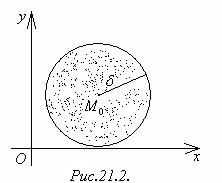Определение.Множество всех точек М(х;у), координаты которых удовлетворяют неравенству 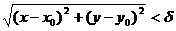, называется −

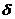окрестностьюточки М₀(х₀;у₀) − это всё внутренние

точки круга с центром М₀ и радиусом 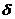(рис.21.2).

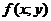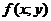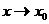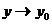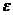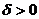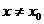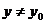Определение.Пусть функция z = определена в некоторой окрестности точки М₀(х₀;у₀), кроме быть может, самой этой точки. Число А называется пределом функцииz = при и (или, что то же самое, при М(х;у) → М₀(х₀;у₀)), если для любого > 0 существует такое, что для всех и из 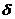−окрестности точки М₀, выполняется неравенство 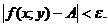Записывают:

А = 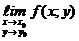или А = .

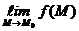Как правило, вычисление пределов функции двух переменных оказывается существенно более трудной задачей 7по сравнению со случаем одной переменной. Причина заключается в том, что на прямой существуют всего 2 направления, по которым аргумент может стремиться к предельной точке − а именно, справа и слева. На плоскости же таких направлений − бесконечное множество, и пределы функции по разным направлениям могут не совпадать.

Определение.Функция z = 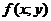называется непрерывной в точке 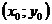, если она:

1) определена в точке ;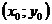

2) имеет конечный предел пр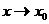и и ;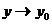

3) этот предел равен значению функции в точке 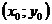, т.е. = .

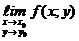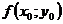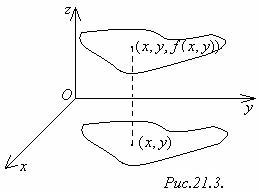Геометрический смысл непрерывности очевиден: график функции z = 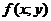в точке 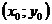представляет собой сплошную, нерасслаивающуюся поверхность. Напомним, что графиком функции z = 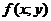называется совокупность точек 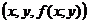трёхмерного пространства (рис.21.3).