Свойства определенного интеграла
1)Определенный интеграл с одинаковыми пределами равен нулю:
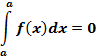
2)При перестановке пределов интегрирования знак интеграла меняется на противоположный:
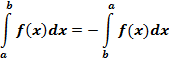
3) Отрезок интегрирования можно разбивать на части:
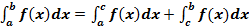 , гдеa<c<b
, гдеa<c<b
4) Постоянный множитель можно выносить за знак интеграла:
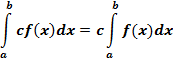
5) Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от всех слагаемых:
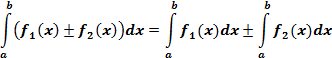
Основные формулы интегрирования
1. 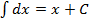
2. 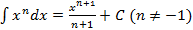
3. 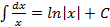
4. 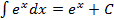
5. 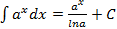
6. 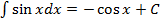
7. 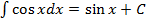
8. 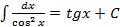
9. 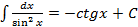
10. 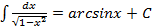
11. 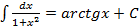
12. 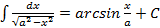
13. 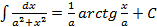
14. 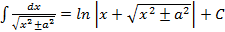
Задания
Вычислить определенные интегралы
Вариант №1.
1. 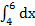
2. 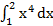
3. 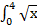 dx
dx
4. 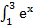 dx
dx
5. 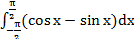
6. 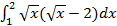
7. 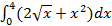
8. 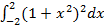
9. 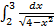
Вариант №2.
1. 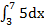
2. 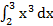
3. 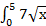 dx
dx
4. 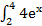 dx
dx
5. 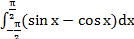
6. 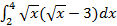
7. 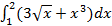
8. 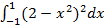
9. 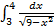
Вариант №3.
1. 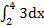
2. 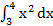
3. 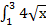 dx
dx
4. 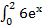 dx
dx
5. 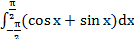
6. 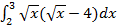
7. 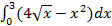
8. 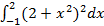
9. 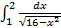
Найти площадь криволинейной трапеции, изображённой на рисунке.
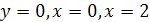 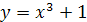 8.1 8.1 | 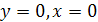 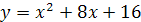 8.6 8.6 | 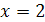 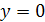 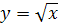 8.11 8.11 |
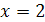 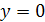 8.2 8.2 | 8.7 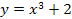 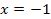 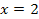 | 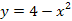 8.12 8.12 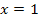 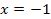 |
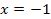 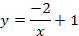 8.3 8.3 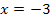 | 8.8 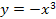 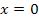 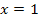 | 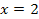 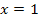 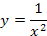 8.13 8.13 |
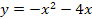 8.4 8.4 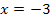 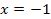 | 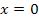 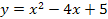 8.9 8.9 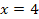 | 8.14 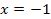 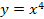 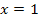 |
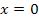 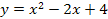 8.5 8.5 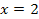 | 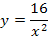 8.10 8.10 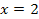 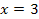 | 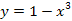 8.15 8.15 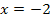 |
Содержание отчета
Отчет должен содержать:
5. Название работы.
6. Цель работы.
7. Задания с решениями.
8. Вывод по работе.
6. Контрольные вопросы:
1)Записать формулу Ньютона- Лейбница.
2)Сформулировать порядок вычисления определенного интеграла.
3)Сформулировать основные свойства определенного интеграла.
Практическая работа № 9.
Нахождение общего и частного решения дифференциальных уравнений.
1. Цель работы: Научиться решать дифференциальные уравнения с разделяющимися переменными и линейные дифференциальные уравнения первого порядка.
2. Оборудование:Таблица неопределенных интегралов, инструкционные карты.
3. Теоретические сведения:
Дифференциальным уравнением называется уравнение, связывающее независимую переменную, искомую функцию, ее производную (или дифференциал аргумента и дифференциал функции).
Дифференциальное уравнение называется обыкновенным, если искомая функция зависит только от одного независимого переменного.
Если дифференциальное уравнение содержит производную или дифференциал не выше первого порядка, то оно называется дифференциальным уравнением первого порядка. Общий вид такого уравнения 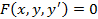 , где y=f(x)- искомая неизвестная функция,
, где y=f(x)- искомая неизвестная функция, 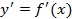 ее производная по x, а F- заданная функция переменных x,y,
ее производная по x, а F- заданная функция переменных x,y, 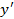 .
.
Общим решением дифференциального уравнения первого порядка называется функция 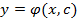 от x и произвольной постоянной С, обращающая это уравнение в тождество по x.
от x и произвольной постоянной С, обращающая это уравнение в тождество по x.
Общее решение, записанное в неявном виде Φ(x,y,C)=0 называется общим интегралом.
Частным решением уравнения 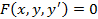 , называется интеграл, полученный из общего интеграла при фиксированном значении С :Φ(x,y,
, называется интеграл, полученный из общего интеграла при фиксированном значении С :Φ(x,y, 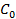 )=0
)=0
Дифференциальные уравнения с разделяющимися переменными
Общий вид такого уравнения: 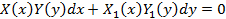 , где
, где 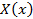 ,
, 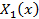 - функции только от x,
- функции только от x, 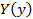 ,
, 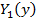 - функции только от y.
- функции только от y.
Поделив обе части уравнения на произведение 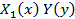 ≠0, получим уравнение с разделяющимися переменными:
≠0, получим уравнение с разделяющимися переменными:
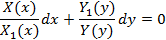
Общий интеграл этого уравнения имеет вид:
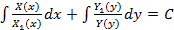 .
.
Линейные дифференциальные уравнения первого порядка имеют вид
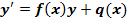 , где f(x) и q(x)- заданные функции от x.
, где f(x) и q(x)- заданные функции от x.
Основные формулы интегрирования
1. 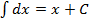
2. 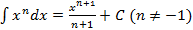
3. 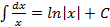
4. 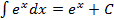
5. 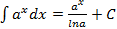
6. 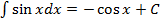
7. 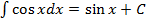
8. 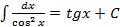
9. 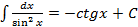
10. 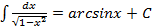
11. 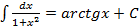
12. 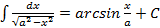
13. 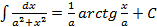
14. 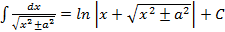
Задания
Найти общее и частное решения дифференциальных уравнений
Вариант №1.
1. 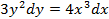
2. 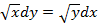
3. 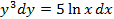
4. 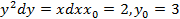
5. 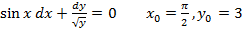
6. 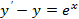
7. 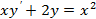
Вариант №2.
1. 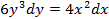
2. 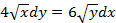
3. 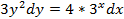
4. 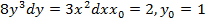
5. 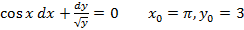
6. 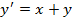
7. 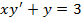
Содержание отчета
Отчет должен содержать:
1.Название работы.
2.Цель работы.
3.Задания с решениями.
4.Вывод по работе.
6. Контрольные вопросы:
1) Какое уравнение называют дифференциальным?
2) Какое уравнение называют дифференциальным уравнением первого порядка?
3) Что называют общим решением дифференциального уравнения, частным решением?
4) Записать вид дифференциального уравнения с разделяющимися переменными, линейного дифференциального уравнения первого порядка.
Практическая работа № 10.
