Тема. Прямые линии и плоскости. Кривые второго порядка. Комплексные числа.
Прямая на плоскости и в пространстве. Плоскость. Классификация кривых второго порядка, приведение к каноническому виду, построение. Комплексные числа, действия над ними. Нахождение корней алгебраических уравнений на множестве комплексных чисел.
2.3. Виды самостоятельной работы студентов.
Самостоятельная работа студентов предполагает изучение теоретического материала и выполнение контрольной работы.
3. Рекомендуемая литература.
Основная литература:
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. Учебник для вузов. -М: ФИЗМАТЛИТ, 2005. -304с.
2. Владимирский Б.М., Горстко А.Б., Ерусалимский Я.М. Математика. Общий курс: Учебник для бакалавров. –СПб.: Изд-во «Лань», 2008. -960с. ISBN: 978-5-8114-0445-2 (http://e.lanbook.com/books/element.php?pl1_id=634).
3. Ильин В.А., Ким Г.Д. Линейная алгебра и аналитическая геометрия. –М.: Велби: Проспект, 2007.
4. Мышкис А.Д. Лекции по высшей математике: учебное пособие. –СПб.: Лань, 2009. -640с.
5. Шипачев В.С. Высшая математика. Учебник для вузов. -М. Высшая школа, 2005. -479 с.
6. Шипачёв В.С. Задачи по высшей математике: Учеб. пособие для вузов. – М.: Высш. шк., 2005. -304с.
Дополнительная литература:
- Беклемишева Л.А., Беклемишев Д.В., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре: Учебное пособие. –СПб.: Изд-во «Лань», 2008. -496с. ISBN 978-5-8114-0861-0. Режим доступа: http://e.lanbook.com/books/element.php?pl1_id=76.
- Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х частях. Учеб. пособие для вузов. Часть I: -М: Высшая школа, 2008. -304с.
- Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика: решебник. -М.: ФИЗМАТЛИТ, 2003. -368с.
- Письменный Д.Т. Конспект лекций по высшей математике: В 2-х ч. Ч.1: Тридцать пять лекций.- 9-е изд.- М.: Айрис-пресс, 2008.
- Соловьёв И.А., Шевелёв В.В., Червяков А.В., Репин А.Ю. Практическое руководство к решению задач по высшей математике. Линейная алгебра, векторная алгебра, аналитическая геометрия, введение в математический анализ, производная и её приложения: Учебное пособие. –СПб.: Изд-во «Лань», 2009. -320с. ISBN: 978-5-8114-0751-4. (http://e.lanbook.com/books/element.php?pl1_id=374).
- Сборник задач по математике для втузов. Ч.1. Линейная алгебра и основы математического анализа: Учеб. пособие для втузов /Болгов В.А., Демидович Б.П., Ефимов А.В. и др. Под общ. ред. А.В. Ефимова и Б.П. Демидовича. -М: Наука, 1993. – 480с.
- Сборник задач по математике для вузов. Учеб. пособие для студентов вузов. /Абрамова В.В., Бикчурина Л.Ж., Валеева М.И. и др.; под ред. Котляра Л.М., Углова А.Н.; 5-е изд., перераб. и доп. -Наб. Челны: ИНЭКА, 2006. – 472с. (Гриф Министерства образования и науки РФ)
4. Методические указания по изучению дисциплины.
В процессе изучения данной дисциплины студенты должны сначала изучить теоретический материал и выработать навыки решения типовых задач, используя рекомендованную литературу, а затем выполнить по одной контрольной работе в каждом из семестров обучения (задания для контрольной работы приведены в разделе 5.1).
При выполнении контрольной работы необходимо придерживаться указанных ниже правил:
1.Контрольная работа должна быть выполнена студентом в отдельной ученической тетради с полями не менее 3 см для замечаний преподавателя.
2.На обложке тетради указываются: название дисциплины; номер варианта и номера решаемых задач; Ф.И.О. студента, выполнившего работу, его номер группы и номер зачетной книжки; Ф.И.О. преподавателя, проверяющего работу (образец оформления обложки приведён в Приложении 6.4).
3.Номер варианта соответствует номеру студента в списке группы.
4.Номера решаемых задач выбираются из ТАБЛИЦЫ НОМЕРОВ ВЫПОЛНЯЕМЫХ ЗАДАНИЙ (Приложение 6.5).
5.Условия задач переписываются полностью, без сокращения слов, после чего приводится их подробное решение (чертежи можно выполнять аккуратно от руки). В конце решения приводится ответ.
6.В работу должны быть включены все задачи, указанные в задании, строго по порядку номеров. Контрольные работы, содержащие не все задания, а также задачи не своего варианта, не зачитываются.
7.Если в работе имеются ошибки, студент должен выполнить все требования преподавателя, изложенные в рецензии, и сдать работу с исправлениями на повторную проверку.
8.Никакие исправления в тексте уже проверенной работы не допускаются, все исправления записываются после рецензии преподавателя с указанием номера задачи, к которой относятся дополнения и исправления.
9.Работа может быть выполнена заново в случае выявления серьёзных замечаний и ошибок.
10.В конце тетради рекомендуется оставлять несколько чистых страниц для дополнений и исправлений.
После проверки контрольная работа предъявляется к защите. На защите студент должен показать свое умение решать задачи, подобные тем, что имеются в его контрольной работе.
Образец решения типового варианта контрольной работы приведён в Приложении 6.1.
5. Материалы для контроля знаний студентов.
Итоговой формой контроля знаний является экзамен (зачёт) в конце первого семестра обучения. На экзамене (зачёте) студент должен показать знание теоретических основ курса в объёме вопросов, приведённых в разделе 5.2и умение решать задачи, подобные тем, что имеются в его контрольной работе.
Задания для контрольной работы.
1 – 10.Вычислить определитель:
а)непосредственным разложением по 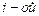 строке;
строке;
б)непосредственным разложением по 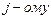 столбцу.
столбцу.
1. 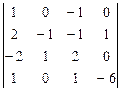 2.
2. 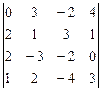 3.
3. 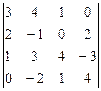
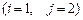
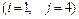
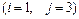
4. 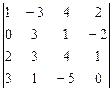 5.
5. 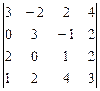 6.
6. 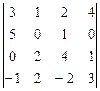
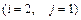
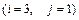
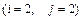
7. 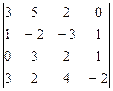 8.
8. 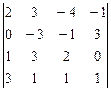 9.
9. 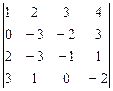
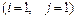
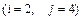
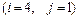
10. 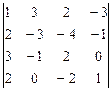
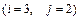
11 – 20.Найтиматрицу 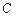 , если
, если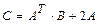 .
.
11. 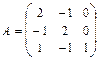 ,
, 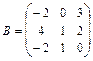 12.
12. 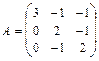 ,
, 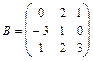
13. 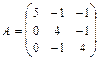 ,
, 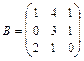 14.
14. 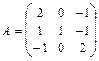 ,
, 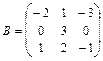
15. 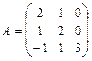 ,
, 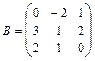 16.
16. 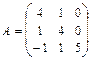 ,
, 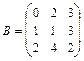
17. 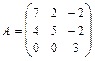 ,
, 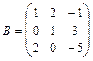 18.
18. 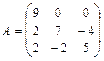 ,
, 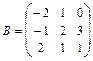
19. 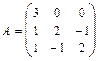 ,
, 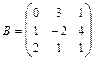 20.
20. 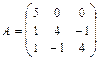 ,
, 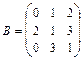 .
.
21 – 30. Дана система трех линейных уравнений с тремя неизвестными. Требуется: а) найти решение системы методом Крамера;
б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса.
21. 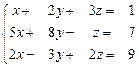 22.
22. 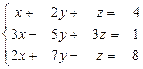
23. 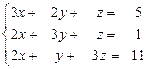 24.
24. 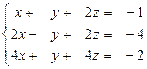
25. 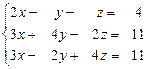 26.
26. 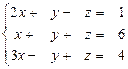
27. 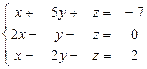 28.
28. 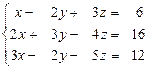
29. 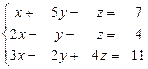 30.
30. 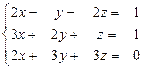
31–40.Найти общее решение системы линейных уравнений методом Гаусса:
31. 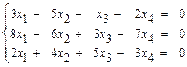 32.
32. 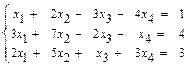
33. 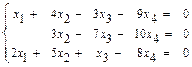 34.
34. 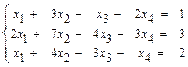
35. 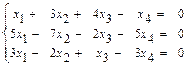 36.
36. 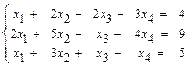 37.
37. 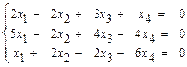 38.
38. 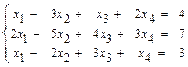
39. 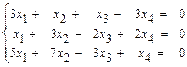 40.
40. 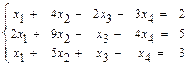
41 – 50.Требуется:
а)найтисобственные числа и векторы матрицы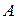 ;
;
б)исследовать квадратичную форму на знакоопределённость (по критерию Сильвестра).
41. а) 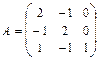 б)
б) 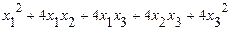
42. а) 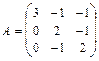 б)
б) 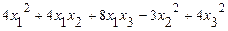
43. а) 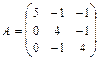 б)
б) 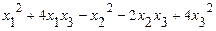
44. а) 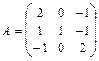 б)
б) 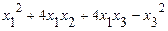
45. а) 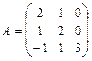 б)
б) 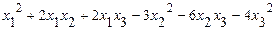
46. а) 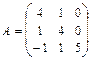 б)
б) 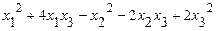
47. а) 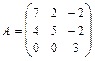 б)
б) 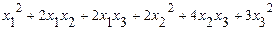
48. а) 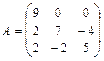 б)
б) 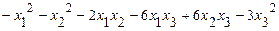
49. а) 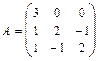 б)
б) 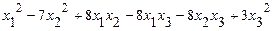
50. а) 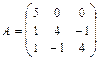 б)
б) 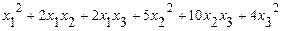
51 – 60.Даны векторы 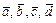 . Показать, что векторы
. Показать, что векторы 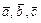 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 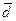 в этом базисе.
в этом базисе.
51. 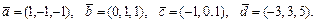
52. 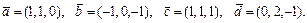
53. 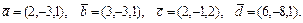
54. 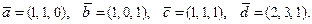
55. 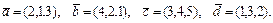
56. 
57. 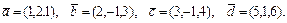
58. 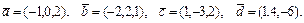
59. 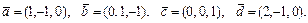
60. 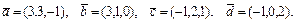
61 – 70.Даны векторы 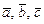 . Требуется:
. Требуется:
а)найти векторы 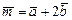 и
и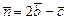 ;
;
б)вычислить скалярное произведение 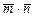 ;
;
в)найти проекцию вектора 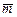 на направление вектора
на направление вектора 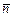 ;
;
г)найтивекторное произведение 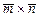 и его модуль
и его модуль 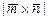 .
.
61. 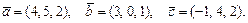
62. 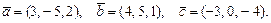
63. 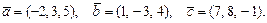
64. 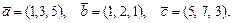
65. 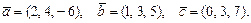
66. 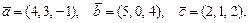
67. 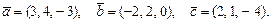
68. 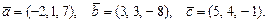
69. 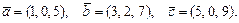
70. 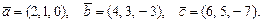
71-80.Даны вершины треугольника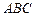 .Требуется найти:
.Требуется найти:
а)длину стороны 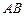 ;б)уравнение стороны
;б)уравнение стороны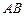 ;
;
в)уравнение медианы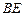 ,проведённой из вершины
,проведённой из вершины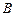 ;
;
г)уравнение высоты 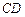 , проведённой из вершины
, проведённой из вершины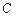 ;
;
д)длину 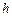 высоты
высоты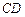 ; е)площадь
; е)площадь 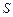 треугольника
треугольника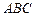 .Сделать чертёж.
.Сделать чертёж.
71. 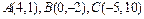 . 72.
. 72. 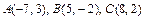
73. 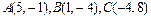 74.
74. 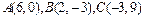
75. 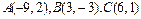 76.
76. 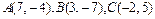
77. 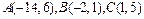 78.
78. 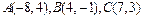
79. 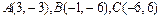 80.
80. 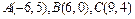
81 – 90.Даны вершины пирамиды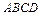 .Требуется найти:
.Требуется найти:
а)длины ребер 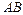 и
и 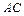 ;б)угол между ребрами
;б)угол между ребрами 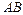 и
и 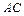 ;
;
в)площадь грани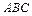 ; г)объем пирамиды
; г)объем пирамиды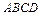 ;
;
д)уравнение плоскости грани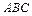 ; е)длину
; е)длину 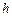 высоты
высоты 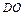 пирамиды.
пирамиды.
81. 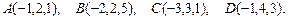
82. 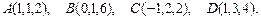
83. 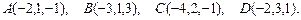
84. 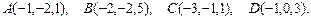
85. 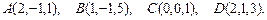
86. 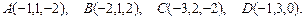
87. 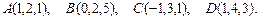
88. 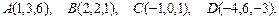
89. 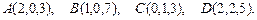
90. 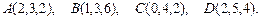
91–100.Установить, какую невырожденную кривую определяет алгебраическое уравнение второго порядка, построить её.
91. 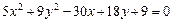 92.
92. 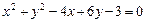
93. 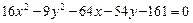 94.
94. 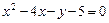
95. 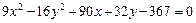 96.
96. 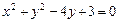
97. 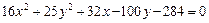 98.
98. 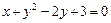
99. 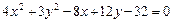 100.
100. 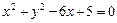
101-110.Даны комплексные числа 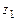 ,
, 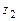 ,
, 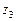 . Требуется: а)вычислить
. Требуется: а)вычислить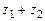 ,
, 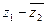 ,
, 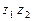 ,
, 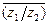 ; б)представить комплексное число
; б)представить комплексное число 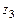 в тригонометрической форме, вычислить
в тригонометрической форме, вычислить 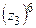 и результат представить в алгебраической форме.
и результат представить в алгебраической форме.
101. 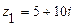 ,
, 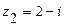 ,
, 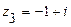 .
.
102. 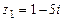 ,
, 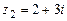 ,
, 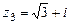 .
.
103. 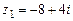 ,
, 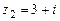 ,
, 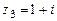 .
.
104. 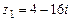 ,
, 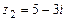 ,
, 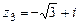 .
.
105. 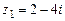 ,
, 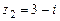 ,
, 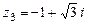 .
.
106. 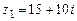 ,
, 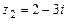 ,
, 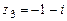 .
.
107. 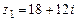 ,
, 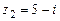 ,
, 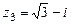 .
.
108. 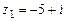 ,
, 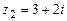 ,
, 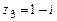 .
.
109. 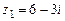 ,
, 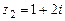 ,
, 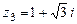 .
.
110. 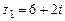 ,
, 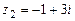 ,
, 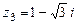 .
.
111-120.Дано алгебраическое уравнение 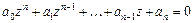 . Требуетсянайти все корни алгебраического уравнения на множестве комплексных чисел.
. Требуетсянайти все корни алгебраического уравнения на множестве комплексных чисел.
111. 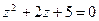 . 112.
. 112. 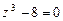 . 113.
. 113. 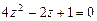 .
.
114. 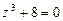 . 115.
. 115. 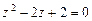 . 116.
. 116. 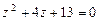 .
.
117. 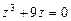 . 118.
. 118. 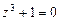 . 119.
. 119. 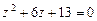 .
.
120. 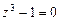 .
.
Вопросы к экзамену (зачёту).
Раздел. Линейная алгебра.
1. Понятие матрицы. Частные виды матриц (квадратная, треугольная, диагональная, нулевая, единичная). Элементарные преобразования матриц. Понятие эквивалентности и равенства матриц.
2. Действия над матрицами (сложение, вычитание, умножение матрицы на число, умножение матрицы на матрицу) и их свойства. Линейная комбинация матриц.
3. Определители 2-ого и 3-егопорядка, их вычисление. Основные свойства определителей.
4. Понятие определителя n-ого порядка. Минор и алгебраическое дополнение элемента определителя. Теорема о разложении определителя по элементам строки или столбца.
5. Понятие системы линейных уравнений (СЛУ). Частные виды СЛУ (квадратная, однородная, неоднородная). Матрица, расширенная матрица, определитель СЛУ.
6. Решение, множество решений СЛУ. Совместность, несовместность, определённость, неопределённость, эквивалентность СЛУ. Элементарные преобразования СЛУ, их основное свойство.
7. Теорема Крамера (о разрешимости СЛУ порядка 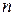 ). Формулы Крамера для решения СЛУ, условия их применимости.
). Формулы Крамера для решения СЛУ, условия их применимости.
8. Метод Гаусса решения СЛУ, условия его применимости. Базисные и свободные переменные. Нахождение общего решения СЛУ. Частные решения СЛУ.
9. Понятие обратной матрицы. Вырожденные и невырожденные матрицы. Теорема о существовании обратной матрицы. Основные способы нахождения обратной матрицы.
10. Матричные уравнения и их решение. Матричная форма записи СЛУ. Матричный способ (метод обратной матрицы) решения СЛУ и условия его применимости.
11. Однородные СЛУ, условия существования их ненулевых решений. Свойства частных решений однородных СЛУ.
12. Понятие линейной независимости и зависимости частных решений однородной СЛУ. Фундаментальная система решений (ФСР), её нахождение. Представление общего решения однородной СЛУ через ФСР.
13. Минор 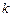 -ого порядка, базисный минор, ранг матрицы. Вычисление ранга матрицы. Критерий совместности СЛУ (теорема Кронеккера-Капелли).
-ого порядка, базисный минор, ранг матрицы. Вычисление ранга матрицы. Критерий совместности СЛУ (теорема Кронеккера-Капелли).
14. Понятие 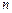 -мерного арифметического вектора. Равенство векторов. Действия над векторами (сложение, вычитание, умножение на число, умножение на матрицу). Линейная комбинация векторов.
-мерного арифметического вектора. Равенство векторов. Действия над векторами (сложение, вычитание, умножение на число, умножение на матрицу). Линейная комбинация векторов.
15. Скалярное произведение арифметических векторов. Длина вектора и угол между векторами. Понятие ортогональности векторов.
16. Система векторов и её линейная комбинация. Понятие линейной зависимости и независимости системы векторов. Теорема о необходимом и достаточном условиях линейной зависимости системы векторов.
17. Понятие векторного пространства 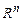 ,евклидова пространства
,евклидова пространства 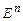 . Базис, канонический базис, ранг
. Базис, канонический базис, ранг 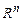 . Разложение вектора в
. Разложение вектора в 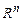 по векторам его базиса, координаты вектора. Теорема о единственности разложения вектора в данном базисе.
по векторам его базиса, координаты вектора. Теорема о единственности разложения вектора в данном базисе.
18. Понятие ортогональной системы векторов, ортогонального базиса. Нахождение координат вектора в ортогональном базисе.
19. Понятие оператора, линейного оператора. Матрица линейного оператора. Сумма (разность) операторов, произведение оператора на число, произведение оператора на оператор, обратный оператор.
20. Понятие собственного числа и собственного вектора оператора. Характеристическое уравнение. Нахождение собственных чисел и векторов оператора.
21. Понятие квадратичной формы. Матрица квадратичной формы. Вырожденная, невырожденная, каноническая, нормальная квадратичная форма. Закон инерции квадратичных форм.
22. Понятие знакоопределённости квадратичной формы. Главные миноры матрицы квадратичной формы. Критерии знакоопределённости квадратичной формы.
Раздел. Векторная алгебра и аналитическая геометрия.
23. Понятие геометрического вектора. Равенство векторов. Противоположный вектор. Орт вектора. Графические правила сложения, вычитания, умножения вектора на число. Проекция вектора на вектор.
24. Коллинеарность и компланарность векторов. Базис и канонический базис плоскости 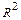 ; базис и канонический базис пространства
; базис и канонический базис пространства 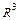 . Координаты вектора.
. Координаты вектора.
25. Понятие декартовой системы координат в 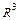 . Радиус-вектор, координаты точки. Вычисление длины и направляющих косинусов вектора; координат вектора, заданного двумя точками; расстояния между точками.
. Радиус-вектор, координаты точки. Вычисление длины и направляющих косинусов вектора; координат вектора, заданного двумя точками; расстояния между точками.
26. Преобразования прямоугольных декартовых систем координат на плоскости (параллельный перенос, поворот, зеркальное отражение). Связь между собой координат произвольной точки в старой и новой системах координат.
27. Скалярное произведение векторов и его свойства. Выражение скалярного произведения через координаты векторов. Вычисление угла между векторами. Условие ортогональности векторов.
28. Векторное произведение векторов, его геометрический смысл и свойства. Выражение векторного произведения через координаты векторов. Условие коллинеарности векторов.
29. Смешанное произведение векторов, его геометрический смысл и свойства. Выражение смешанного произведения через координаты векторов. Условие компланарности векторов.
30. Понятие линии на плоскости. Общее уравнение линии и его нахождение по известному геометрическому свойству её точек. Окружность и её уравнение.
31. Прямая линия на плоскости и её общее уравнение. Нормальный и направляющий векторы прямой. Нахождение уравнения прямой, проходящей через точку перпендикулярно вектору. Построение прямой.
32. Каноническое уравнение прямой; уравнение прямой, проходящей через две точки; уравнение прямой с угловым коэффициентом; уравнение прямой в отрезках. Расстояние от точки до прямой на плоскости. Угол между прямыми на плоскости и его вычисление, условия 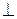 и ½½ прямых.
и ½½ прямых.
33. Понятие поверхности. Общее уравнение поверхности, его нахождение по известному геометрическому свойству её точек. Сфера и её уравнение.
34. Плоскость и её общее уравнение. Нормальный вектор плоскости и его нахождение. Уравнение плоскости, проходящей через точку перпендикулярно вектору. Построение плоскости.
35. Уравнение плоскости, проходящей через три точки; уравнение плоскости в отрезках. Расстояние от точки до плоскости. Угол между плоскостями и его вычисление, условия 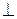 и ½½ плоскостей.
и ½½ плоскостей.
36. Понятие линии в пространстве и её общее уравнение. Понятие прямой линии в пространстве и её общее уравнение. Направляющий вектор прямой и его нахождение.
37. Каноническое уравнение прямой в пространстве; уравнение прямой, проходящей через две точки; параметрические уравнения прямой. Приведение общего уравнения к каноническому.
38. Угол между двумя прямыми в пространстве, между прямой и плоскостью и их вычисление, условия 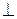 и ½½ двух прямых, прямой и плоскости. Точка пересечения прямой и плоскости.
и ½½ двух прямых, прямой и плоскости. Точка пересечения прямой и плоскости.
39. Кривая 2-ого порядка на плоскости и её общее уравнение. Классификация кривых 2-ого порядка. Приведение уравнения кривых к каноническому виду.
40. Эллипс. Каноническое уравнение эллипса. Построение эллипса. Вершины, полуоси, фокусы, эксцентриситет, общее геометрическое свойство точек эллипса.
41. Гипербола. Каноническое уравнение гиперболы. Построение гиперболы. Вершины, полуоси, фокусы, эксцентриситет, асимптоты, общее геометрическое свойство точек гиперболы.
42. Парабола. Каноническое уравнение параболы. Построение параболы. Вершина, фокус, эксцентриситет, директриса, общее геометрическое свойство точек параболы.
43. Сфера. Эллипсоид. Канонические уравнения и графики.
44. Гиперболоиды (однополостной и двуполостной). Канонические уравнения и графики.
45. Параболоиды (эллиптический и гиперболический). Канонические уравнения и графики.
46. Цилиндры (эллиптический, гиперболический, параболический), их уравнения и графики.
