Прогноз по линейному уравнению регрессии

Установив высокое качество линейной модели, ею можно воспользоваться для прогноза значений результативного признака в пределах изменения факторного признака.

Прогнозное значение 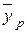определяется путем подстановки в уравнение регрессии 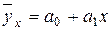соответствующего (прогнозного) значения .

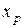Выбор наилучшего вида линии регрессии

Вопрос выбора наилучшей регрессии из нескольких построенных моделей далеко не однозначен. Один из способов, основывающийся на дисперсионном анализе, указан выше. Однако он неявно предполагает выполнение классических условий (Гаусса-Маркова) применения МНК, обеспечивающих состоятельность, несмещенность и эффективность оценок параметров линейного уравнения регрессии. На практике не все условия применения МНК соблюдаются.

Как правило, вид зависимости заранее не известен, ошибки не подчиняются нормальному закону распределения (так как законы больших чисел для конечных выборок не выполняются), случайные ошибки имеются не только на выходе, но и на входе и т.д.

Для учебных целей мы, не вдаваясь в такие детали, будем считать, что наилучший вид регрессии получен в том случае, когда коэффициент детерминации – наибольший.

Однофакторный дисперсионный анализ

Условия применимости

Дисперсионный анализ дает общую схему проверки статистических гипотез, основанную на тщательном изучении различных источников вариации [изменчивости, неоднородности] в сложной ситуации. Он позволяет оценить влияние одного или нескольких факторов на результирующий признак. На практике часто встречается ситуация, когда можно указать один фактор, влияющий на конечный результат, и этот фактор принимает конечное число значений. Такая ситуация может быть проанализирована при помощи однофакторного дисперсионного анализа.

Дисперсионный анализ был предложен Р.Фишером[1] для решения некоторых задач в области биологических исследований, в частности в сельскохозяйственной статистике. В настоящее время дисперсионный анализ определяется как статистический метод, предназначенный для оценки влияния различных факторов на результат эксперимента, в связи с чем, область применения этого метода становится значительно шире. Результатом эксперимента является некоторая случайная величина X, называемая также результативным признаком. На значения случайной величины X влияет фактор A, состоящий из нескольких уровней [групп] A_i , i = 1,…r. Рассмотрим простой пример. Директора фирмы, занимающейся ландшафтным дизайном, интересует зависимость выполненных работ по посадке декоративных кустарников за смену от работающей на посадке бригады. Предположим, что на посадках работают r бригад. Объем выполненных работ является результативным признаком X, работающую бригаду назовем фактором A , а через A_i обозначим i - й уровень [группу] фактора A (i- ю бригаду, i = 1,…r).

В дисперсионном анализе наблюдаемые величины разбиваются на r групп, причем i- я группа содержит выборку из n_i, i=1,…r, величин X_i Î N (a +m_i, s₀) – нормальное распределение с параметрами a +m_i и s₀, где s₀ является постоянной, хотя и неизвестной величиной, не зависящей от i .

Обозначим через x_i,j значение j-й величины в i- й группе. Модель однофакторного дисперсионного анализа можно записать в виде

x_i,j = a + m_i + e_i,j , (39)

где a - генеральное среднее всех мыслимых результатов наблюдений, т.е. M(X) , m_i - эффект влияния на X, вызванный i-м уровнем фактора A, или, иначе, отклонение математического ожидания a_i результативного признака при i-ом уровне фактора от общего математического ожидания a , т.е. m_i = a_i - a; e_i,j - случайный остаток, отражающий влияние на величину x_i,j всех других неконтролируемых факторов.

Основными предпосылками дисперсионного анализа являются:

1) Остатки e_i,j взаимно независимы для любых i и j .

2) e_i,j Î N (0, s₀) и s₀ не зависит от i и j .

Средние значения m_i в (39) могут меняться под влиянием некоторых факторов, например, под влиянием различных способов обработки, различных видов животных или растений, неоднородности почвы и т.д. Целью эксперимента является исследование этой изменчивости средних значений (например, гипотеза H₀ о их равенстве).