Формулы сокращенного умножения
| 1. (a+ b)(a-b) = a2 - b2 2. (a + b)2 = a2 + 2ab + b2 3. (a - b)2 = a2 - 2ab + b2 4. (a + b)( a2 - 2ab + b2) = a3 + b3 5. ( a - b)( a2 + 2ab + b2) = a3 - b3 |
Примеры:
Выполните действия:
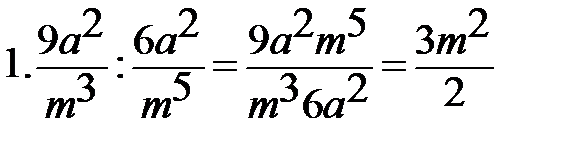
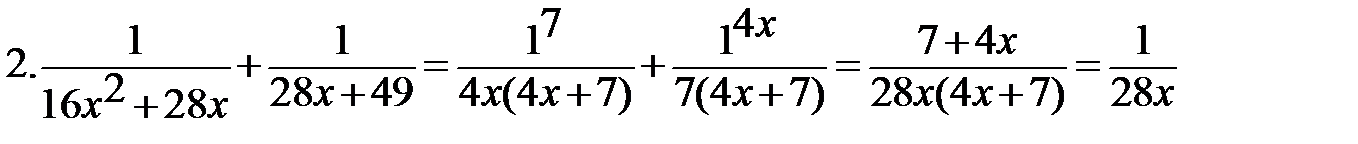
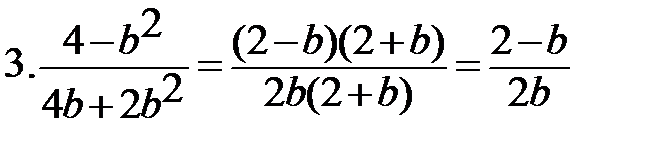
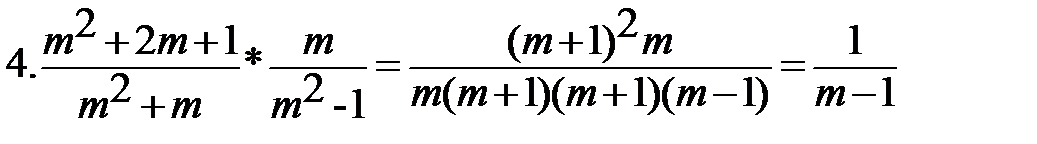

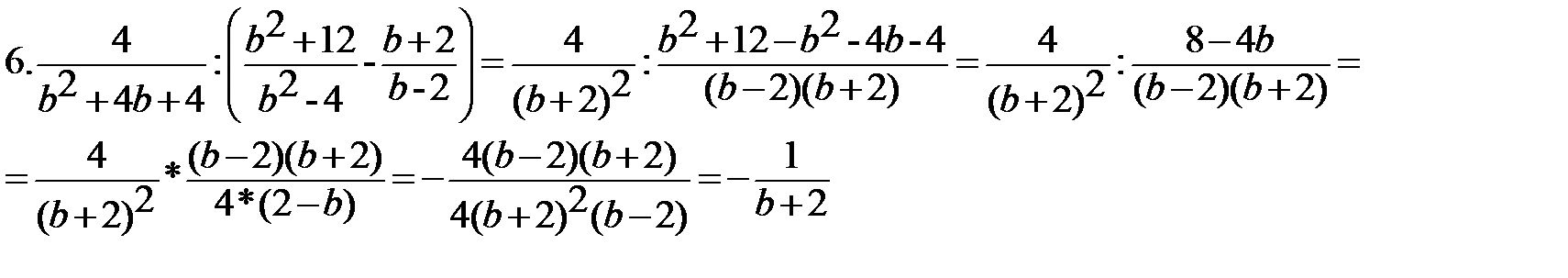
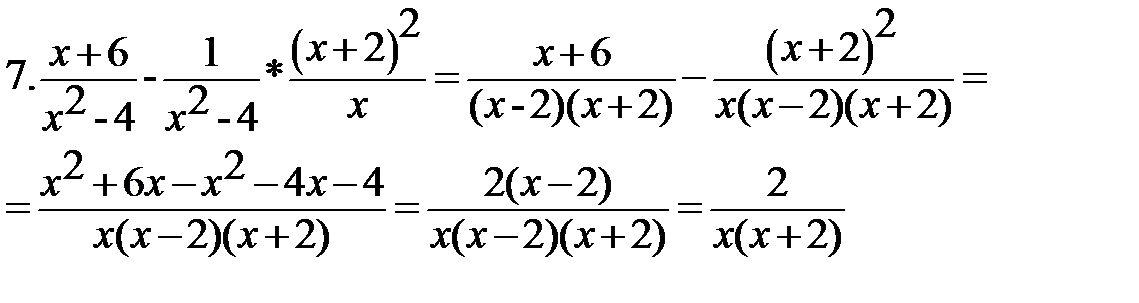
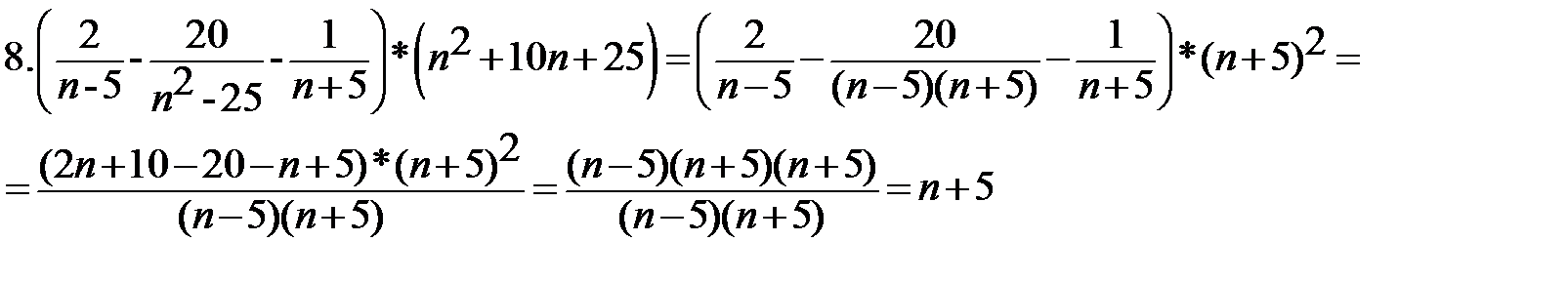
Найти значение выражения при х=80:
9.(9х-3)(9х+3)-81х2+х-39 = 81х2-9-81х2+х-39 = х-48 =80-48=32
х=80
Из материалов ЕГЭ
Упростите данные выражения 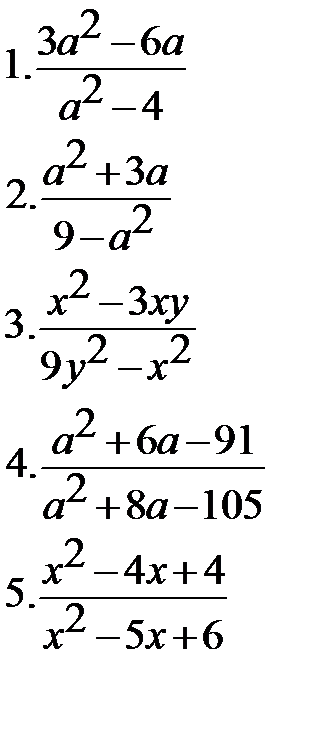 | Найдите значения данных выражений 1.(9х-16)(9х+16)-81х2+6х+30 при х=70 2.(5х-15)(5х+15)-25х2+10х-10 при х=130 3. 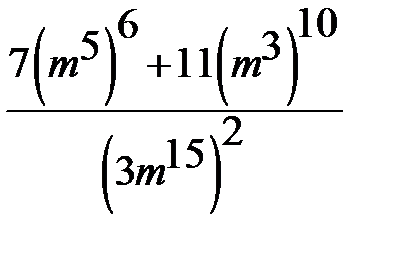 4. вычислите 4. вычислите 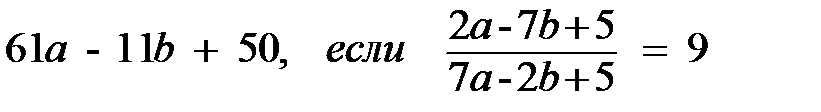 |
1.3.4.Индивидуальные задания – ИЗ-3
| Вариант 1 | Вариант 2 |
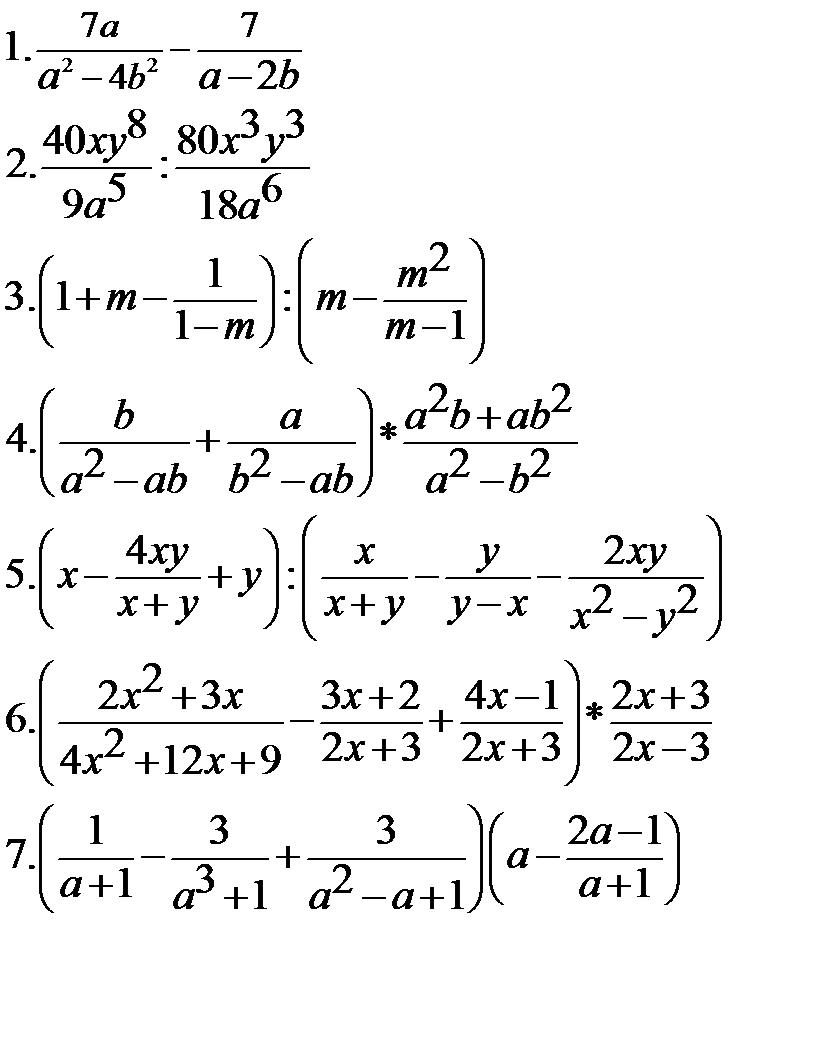 8. 8. 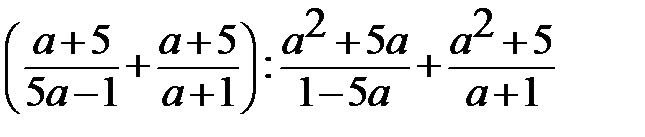 | 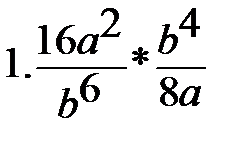 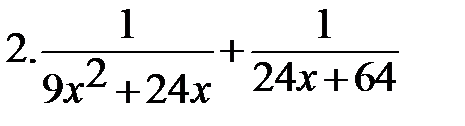 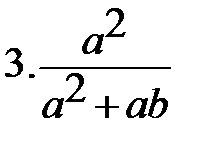 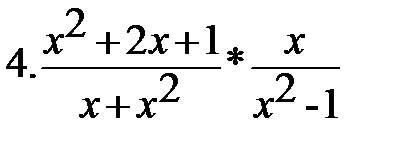 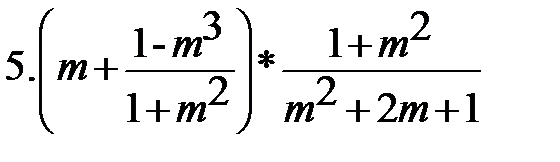 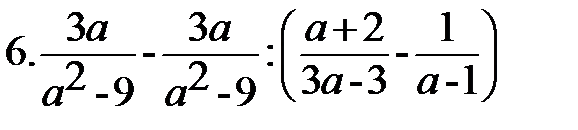 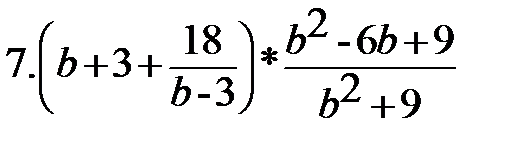 8. 8. 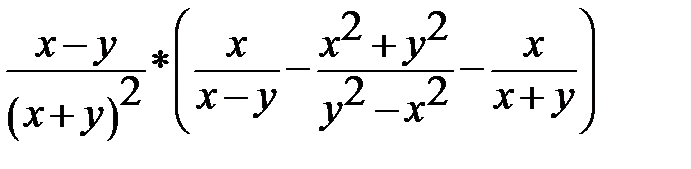 |
Вариант-3 Выполните действия: 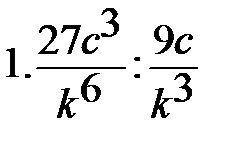 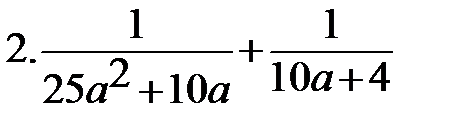 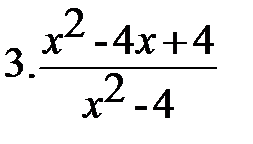 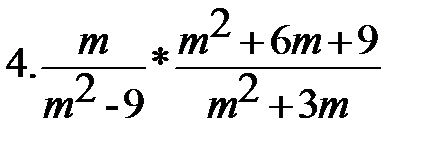 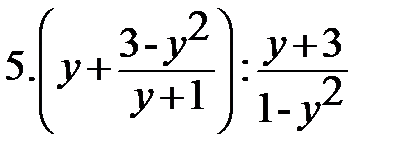 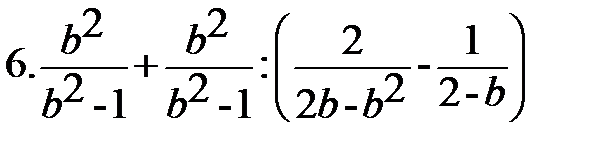 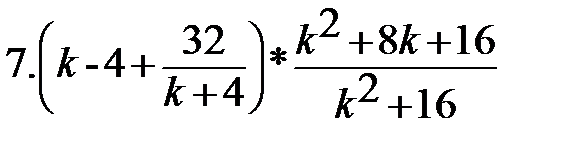 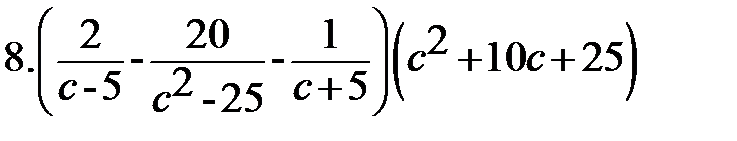 | Вариант-4 Выполните действия: 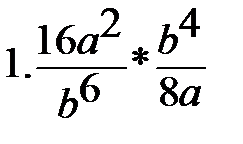 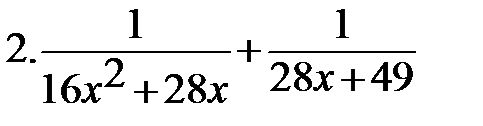 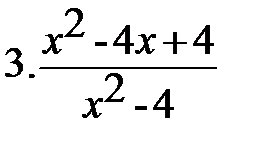 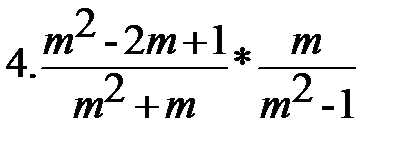 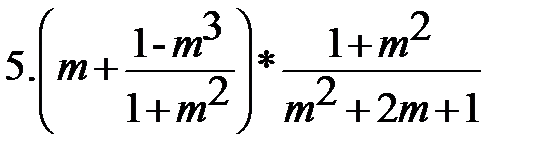 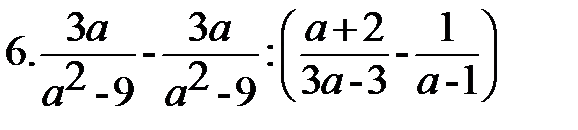 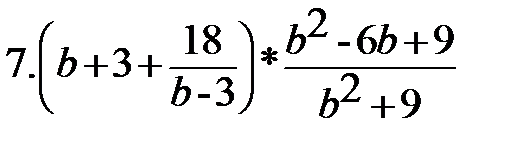 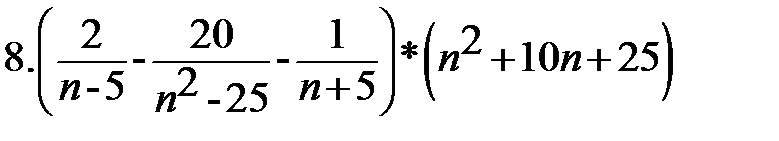 |
Линейные уравнения и неравенства
 | Посредством уравнений, теорем я уйму всяческих решил проблем Чосер, поэт, Англия, XVI век. |  |
Линейные уравнения
Уравнения – это равенства, содержащие неизвестные величины.
Решить уравнение – это значит найти все его корни или доказать, что их нет.
Корнем уравнения называется такое число, при подстановке которого в уравнение получается верное числовое равенство.
Уравнения бывают линейные, квадратные, кубические и т.д., т.е. классификация идет по показателю степени неизвестной величины.
Линейное уравнение – это уравнение 1 степени, т.е. уравнение, в котором неизвестное в 1 степени, оно имеет вид:
| ах+в=0–линейное уравнение с одной переменной, (1) а, в – любые действительные числа. |
Чтобы решить линейное уравнение, как правило, его надо преобразовать, привести к виду(1):
Действия, приводящие к виду (1):
· Раскрытие скобок
· Приведение подобных слагаемых
· Перенос слагаемых из одной части в другую (НЕ ЗАБЫВАЯ МЕНЯТЬ ЗНАК СЛАГАЕМЫХ!!!)
Самое «трудное» уравнение для студентов
☺*x=☼, x= 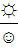 |
Примеры:
1. Простейшие
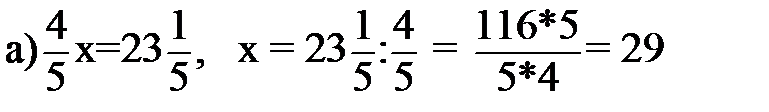
б)47-(3х-9)=110.
3х-9=47-110=-63, 3х=-63+9=-54, х= 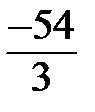 = - 18.
= - 18.
2. со скобками
0,6х-2,5(1+2х)=-0,4х+8,06.
0,6х-2,5-5х=-0,4х+8,06, 0,6х+0,4х-5х=8,06+2,5, -4х = 10,56,
х= - 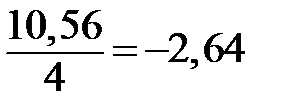
3. Дробные

в)Неизвестное - в знаменателе! 

Самостоятельно:
Решите уравнения
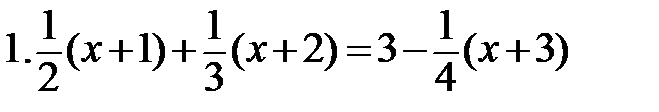 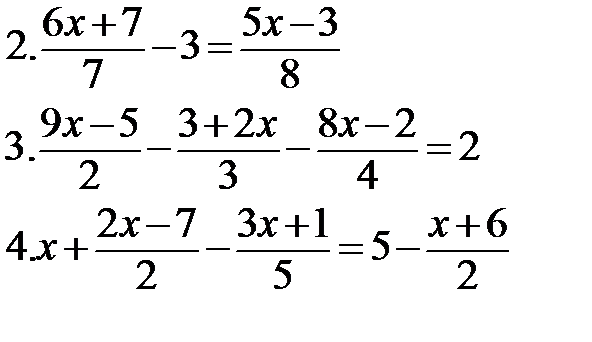 | 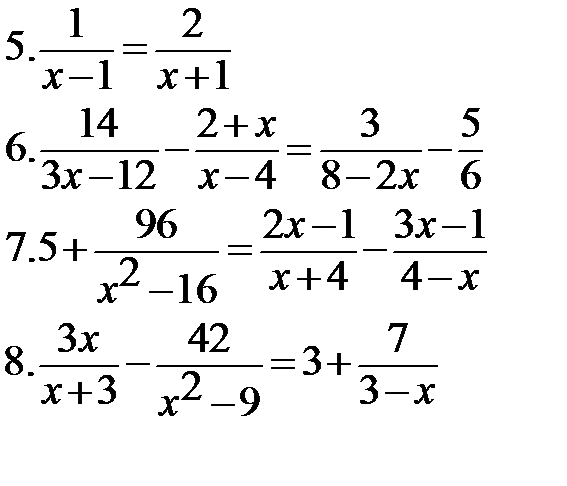 |
Задачи, решаемые с помощью уравнений
1. В одном мешке было 60 кг сахару, а в другом – 80 кг. Из второго мешка взяли сахару в 3 раза больше, чем из первого, и тогда в первом осталось сахару вдвое больше, чем во втором. Сколько кг сахару взяли из каждого мешка?
Решение
1.Пусть х – количество кг сахару, которое взято из первого мешка.
| Было | Взяли | Осталось | |
| х | 60-х | ||
| 3х | 80-3х |
2.По условию: 60-х=2(80-3х), 60-х=160-6х, 5х=100, х=20
Ответ: из первого взяли 20 кг, из второго 60кг.
2.Из фирмы А курьер доставил донесение в фирму В за 35 минут. На обратном пути он увеличил скорость на 0,6км/ч и затратил на дорогу 30 минут. Определите расстояние между фирмами и скорость курьера туда и обратно.
Ответ: 2,1км, 3,6км/ч, 4,2км/ч.
Линейные неравенства
Линейные неравенствас одной переменой – это неравенства вида:
ax≥b или ax≤b, где х-неизвестная,
а и b –любые действительные числа.
Всякое значение переменной, при котором неравенство обращается в верное числовое неравенство, называется решением неравенства.
Решить неравенство это значит найти все решения.
Понятия больше и меньше возникли в связи с необходимостью сравнивать предметы, величины. Понятием неравенства пользовались уже древние греки. Архимед (III век до н.э.), занимаясь вычислением окружности длины, установил, что «периметр всякого круга равен утроенному диаметру с избытком, который меньше седьмой части диаметра, но больше десяти семьдесят первых».
Ряд неравенств приводит в своем трактате «Начала» Евклид.
В «Математическом собрании» Папы Александрийского также использовались знаки неравенства. Однако, все рассуждения проводили словесно, опираясь чаще всего на геометрическую иллюстрацию. Современные знаки неравенств >, < появились лишь в XVII-XVIII веках. Их ввел английский математик Т.Гарриот (1560-1621). Знаки ≥, ≤ ввел французский ученый П.Бугер (1698-1758)



При решении линейных неравенств выполняются те же преобразования, что и при решении уравнений, но возникают некоторые особенности – сложности, которые надо иметь ввиду:
· Если неравенство умножается или делится на отрицательное число, то знак неравенства меняется на противоположный
· Решать неравенства можно методом интервалов, о котором подробно позже.
Примеры:
1.2х≥7+3х, 2х-3х≥7, -х≥7│*(-1), (знак неравенства меняется на противоположный) х≤-7.
2.1,5х≥18
3.- 4х≤17+6х
4.При каких значениях «а» выражение 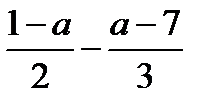 принимает отрицательные значения?
принимает отрицательные значения?
Условие означает, что должно выполняться неравенство: 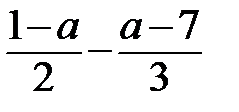 ˂0│*6,
˂0│*6,
3-3а-2а+14˂0 (почему знак неравенства не изменился?), -5а˂-17│*(-1), 5а˃17(почему знак неравенства изменился?), а˃17/5.
5. При каких значениях «х» выражение 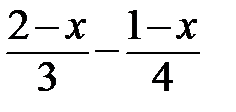 принимает положительные значения?
принимает положительные значения?
6.Решите двойное неравенство:
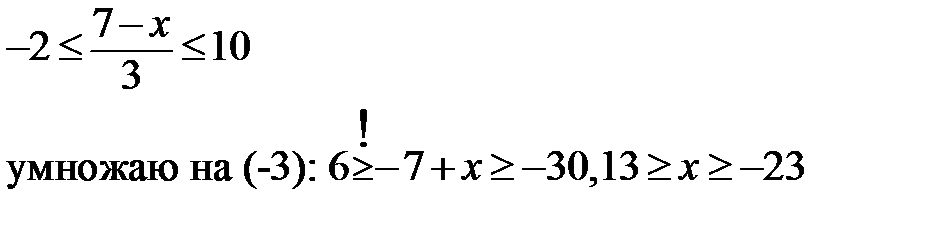
Или двойное неравенство можно записать в виде системы 2 неравенств: 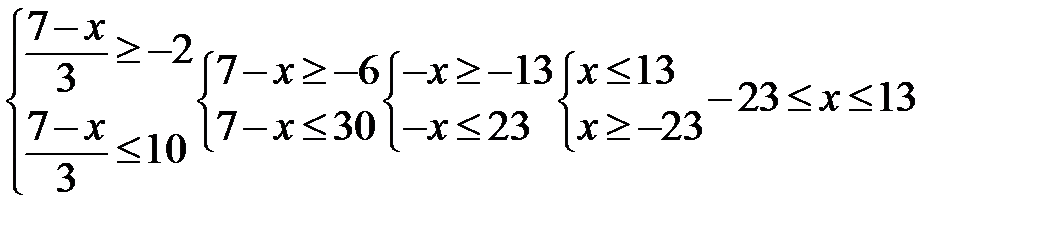
Ответ: -23≤х≤13
7. 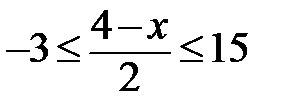
Самостоятельно:
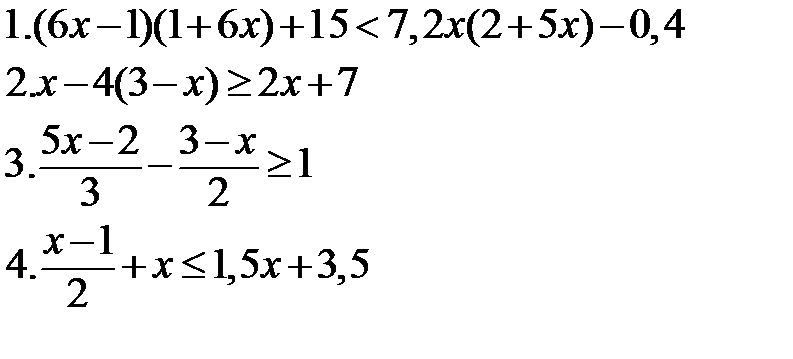 |   |
1.4.4. Индивидуальные задания
(Номер варианта равен остатку от деления номера по списку на 6)
| 1 вариант | 2 вариант |
| ИЗ-4: Линейные уравнения и неравенства | ИЗ-4: Линейные уравнения и неравенства |
Ответьте на вопросы: 1.Что называется уравнением? 2.Какое уравнение называется линейным? 3. Что значит - решить уравнение? 4.Что называется корнем уравнения? 5.Какую особенность имеет решение неравенств? Решите уравнения: 5.21-(5х-11)=12 6.(х+17)*12=804 7.0,3х-1,5(0,2х+4)=⅔*х-8,02 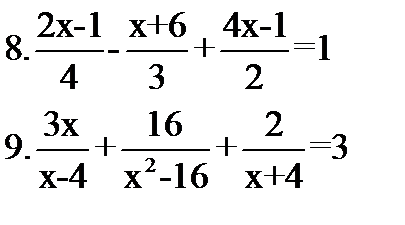 Решите неравенство: 10.5(2-3х)-4(х-7)+3(1+4х)≤10 Решите неравенство: 10.5(2-3х)-4(х-7)+3(1+4х)≤10 | Ответьте на вопросы: 1.Что называется уравнением? 2.Какое уравнение называется линейным? 3. Что значит - решить уравнение? 4.Что называется корнем уравнения? 5.Какую особенность имеет решение неравенств? Решите уравнения: 5.3-(4+3х)-14=0 6.13*(4-х)=26 7.5(0,4х-1)-0,4х=-21 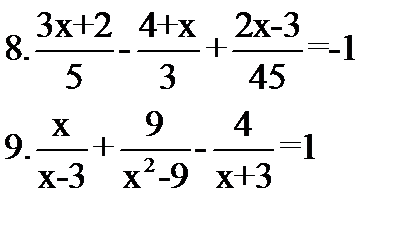 Решите неравенство: 10.(3-2х)*4+(х-2)*3-3(-х-2)≥-2 Решите неравенство: 10.(3-2х)*4+(х-2)*3-3(-х-2)≥-2 |
| 3 вариант | 4 вариант |
| ИЗ-4: Линейные уравнения и неравенства | ИЗ-4: Линейные уравнения и неравенства |
Ответьте на вопросы: 1.Что называется уравнением? 2.Какое уравнение называетсялинейным? 3. Что значит - решить уравнение? 4.Что называется корнем уравнения? 5.Какую особенность имеет решение неравенств? Решите уравнения: 5.3-4(х+2)-(7-2х)=6 6. (5-х)*4=-16 7.0,5х-3,5(4-3х)=⅜*х-2 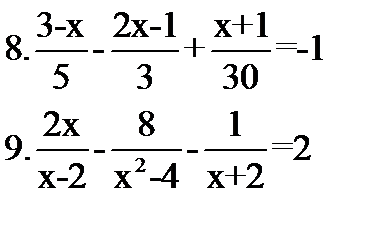 Решите неравенство: 10.3(х-4)-2(8+3х)-2(-1-х)≤ -3 Решите неравенство: 10.3(х-4)-2(8+3х)-2(-1-х)≤ -3 | Ответьте на вопросы: 1.Что называется уравнением? 2.Какое уравнение называется линейным ? 3. Что значит - решить уравнение? 4.Что называется корнем уравнения? 5.Какую особенность имеет решение неравенств? Решите уравнения: 5.17-2(4х+9)-(5-11х)=-15 6.21*(5-13х)=-441 7.0,9х+4,5(1-2х)=-3,6 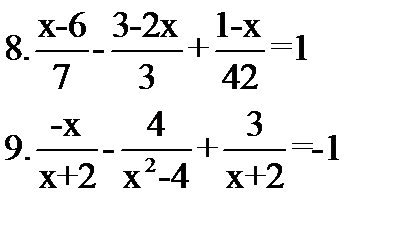 Решите неравенство: 10.2(5-х)- (-х+6)*3-5(2х+1)≥14 Решите неравенство: 10.2(5-х)- (-х+6)*3-5(2х+1)≥14 |
| 5 вариант | 6 вариант |
| ИЗ-4: Линейные уравнения и неравенства | ИЗ-4: Линейные уравнения и неравенства |
Ответьте на вопросы: 1.Что называется уравнением? 2.Какое уравнение называется линейным? 3. Что значит - решить уравнение? 4.Что называется корнем уравнения? 5.Какую особенность имеет решение неравенств? Решите уравнения: 5.1-(2х-7)-15=0 6.(х-5)*27=351 7.0,3х-2,5(0,1х-3)=-  х+3,01 х+3,01 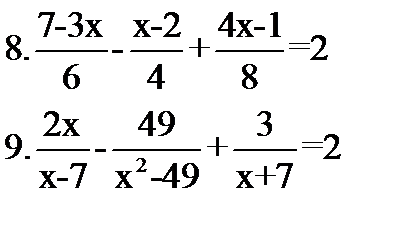 Решите неравенство: 10.(х-1)*3-(7х+9)*2-(3-х)*4≥-5 Решите неравенство: 10.(х-1)*3-(7х+9)*2-(3-х)*4≥-5 | Ответьте на вопросы: 1.Что называется уравнением? 2.Какое уравнение называется линейным? 3. Что значит – решить уравнение? 4.Что называется корнем уравнения? 5.Какую особенность имеет решение неравенств? Решите уравнения: 5.23-2(х+4)-3(5-3х)=-35 6.-43(9х+2)=473 7.0,6х-2,5(1+2х)=-0,4х+8,04 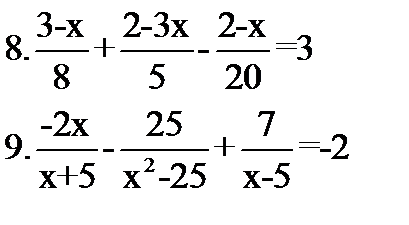 Решите неравенство: 10.4(3-2х)-2(7+3х)-5(1-х)≤11 Решите неравенство: 10.4(3-2х)-2(7+3х)-5(1-х)≤11 |
Из материалов ЕГЭ
Решите уравнения:
1.4-2х=-4х+5 2.5х-2(7+5х)=-4х-10 3. 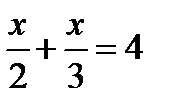 4. 4. 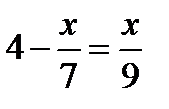 5. 5. 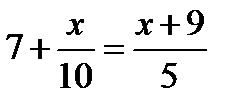 6. 6. 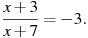 7. 7. 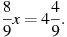 8. 8. 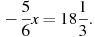 | 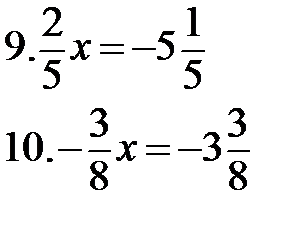 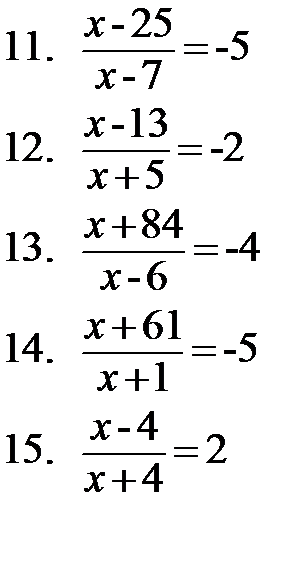 |
Решите задачи:
1.Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой 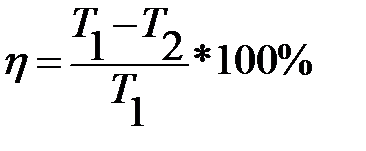 , где Т1 – температура нагревателя (в градусах Кельвина), Т2 – температура холодильника. При какой минимальной температуре нагревателя Т1 КПД двигателя будет не меньше 45%, если температура холодильника Т2=275К ? Ответ выразите в градусах Кельвина. (500К)
, где Т1 – температура нагревателя (в градусах Кельвина), Т2 – температура холодильника. При какой минимальной температуре нагревателя Т1 КПД двигателя будет не меньше 45%, если температура холодильника Т2=275К ? Ответ выразите в градусах Кельвина. (500К)
Решение
(задача на решение линейного неравенства)
1. По условию КПД ≥45%. Это означает, что 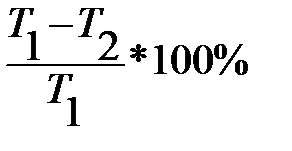 ≥45%. Это неравенство можно немного преобразовать: (1-
≥45%. Это неравенство можно немного преобразовать: (1- 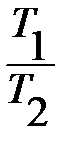 )*100≥45 или с учетом Т2=275К: 1-
)*100≥45 или с учетом Т2=275К: 1- 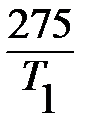 ≥0,45,
≥0,45, 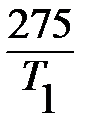 ≤0,55, Т1≥
≤0,55, Т1≥ 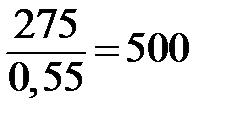 , Т1≥500К. Минимальное значение – 500К.
, Т1≥500К. Минимальное значение – 500К.
2. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой 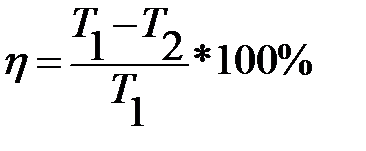 , где Т1 – температура нагревателя (в градусах Кельвина), Т2 – температура холодильника. При какой минимальной температуре нагревателя Т1 КПД двигателя будет не меньше 35%, если температура холодильника Т2=260К? Ответ выразите в градусах Кельвина. (400К)
, где Т1 – температура нагревателя (в градусах Кельвина), Т2 – температура холодильника. При какой минимальной температуре нагревателя Т1 КПД двигателя будет не меньше 35%, если температура холодильника Т2=260К? Ответ выразите в градусах Кельвина. (400К)
Метод интервалов
Метод интервалов – универсальный метод решения неравенств. Он может применяться в неравенствах, в которых правая часть равна 0, а левая представлена (или может быть представлена) в виде дроби или произведения, т.е. 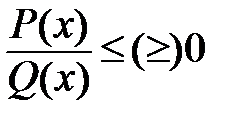 или Р(х)*Q(x)≤(≥)0
или Р(х)*Q(x)≤(≥)0
1.5.1.Алгоритм:
1.Найти нули числителя и знаменателя (или сомножителей), решив уравнения 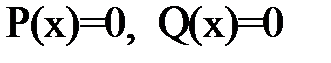
2. Нанести их на числовую ось, отметить их кратность (если (х-2)3 =0, то
число 2-корень нечётной кратности, если (х-2)6 =0, то число 2-корень чётной кратности).
3. Вычислить знак левой части на каждом из полученных промежутков, начиная со знака + и дальше расставляя с учётом кратности корней:
1) если нуль чётной кратности, то не меняя знака
2) если нуль нечётной кратности, то чередуя знаки.
4. Выбрать промежутки, соответствующие знаку неравенства: “>” - “ +”
“<” - “ - “.
5. Записать ответ.
Замечания:
1 Р(х) и Q(x) следует разложить на множители вида (х-а)к .
2. Если левая часть содержит множитель (а-х)к, то следует его заменить множителем (х-а)к с учётом кратности: т.е.(2-х)4=(х-2)4, .(2-х)3= - (х-2)3.
1.5.2.Примеры:
1.

+ - +
-5 2
3.Т.к. знак данного неравенства ˃, то выбираю промежутки, на которых знак +:
Ответ: (-∞;-5) и (2;+∞)
2.
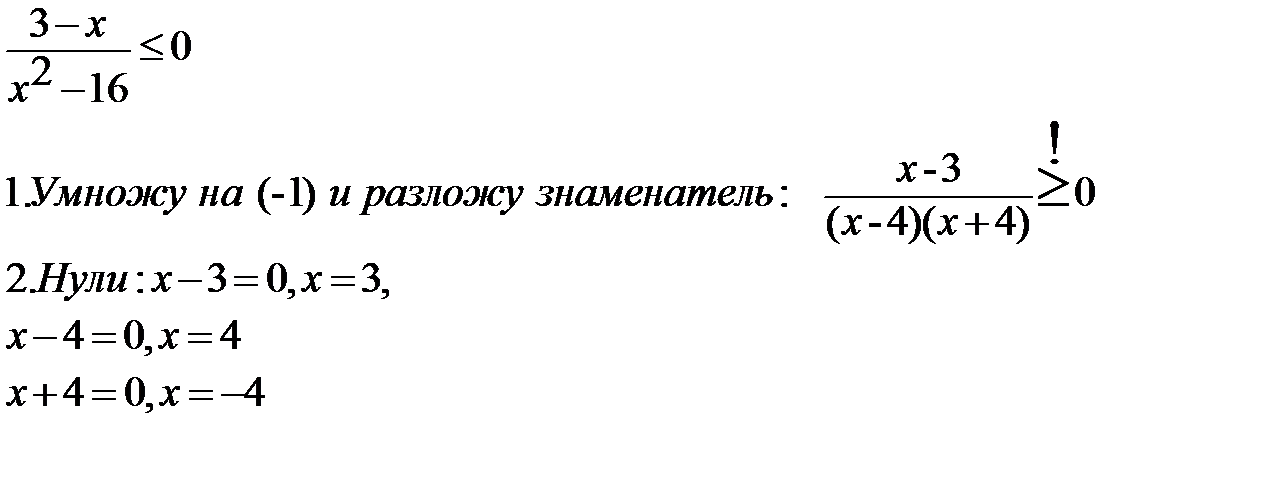
3.
- + - +
-4 3 4
Ответ: (-4;3]  (4;+∞)
(4;+∞)
3.х3-8х2-33х≥0
1. Разложу на множители левую часть: х( х2-8х-33)≥0, х(х+3)(х-11) ≥0.
2. Нули: х=0, х=-3, х=11
3.
- + - +
-3 0 11
Ответ: [-3;0]  [11;+∞)
[11;+∞)
4.
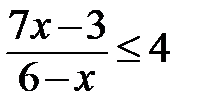
1. Преобразую:
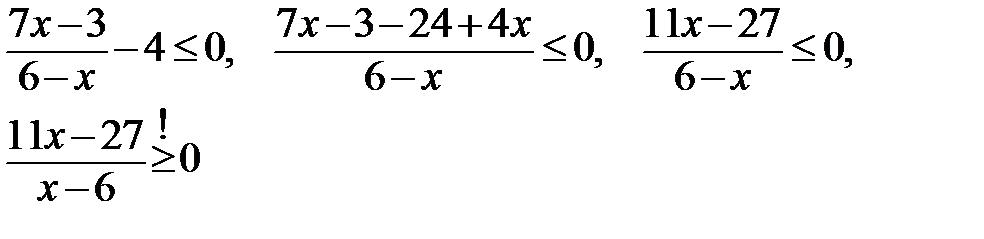
2. Нули: 11х-27=0, 11х=27,х= 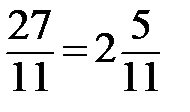
х-6=0,х=6
3.
+ - +
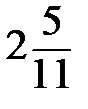 6
6
Ответ: (-∞; 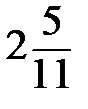 ]
]  (6;+∞)
(6;+∞)
Потренируйтесь!
5. (х-2)(х-3)2(х-4)3≥0 6. 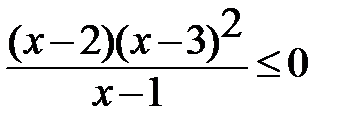 7. 7. 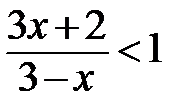 | 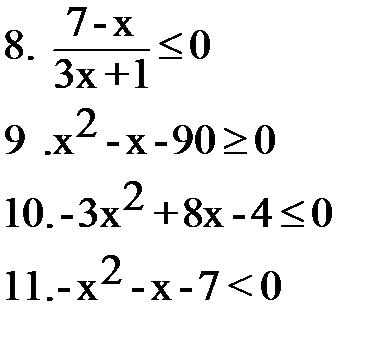 |
!!! 12. 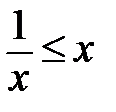 |
1.5.3. Индивидуальные задания
(Номер варианта равен остатку от деления номера по списку на 6)
| ИЗ-5: Метод интервалов | ИЗ-5: Метод интервалов | ИЗ-5: Метод интервалов | ИЗ-5: Метод интервалов |
| 1 вариант | 2 вариант | 3 вариант | 4 вариант |
Решите неравенства  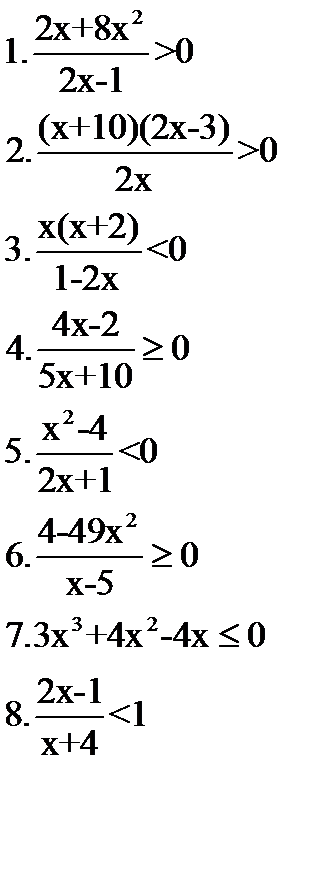 | Решите неравенства 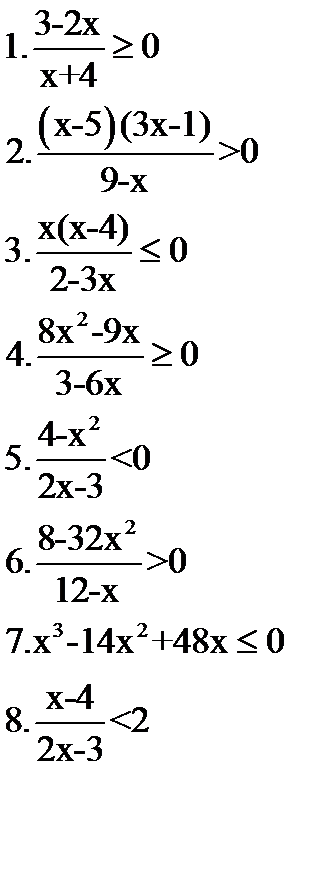 | Решите неравенства 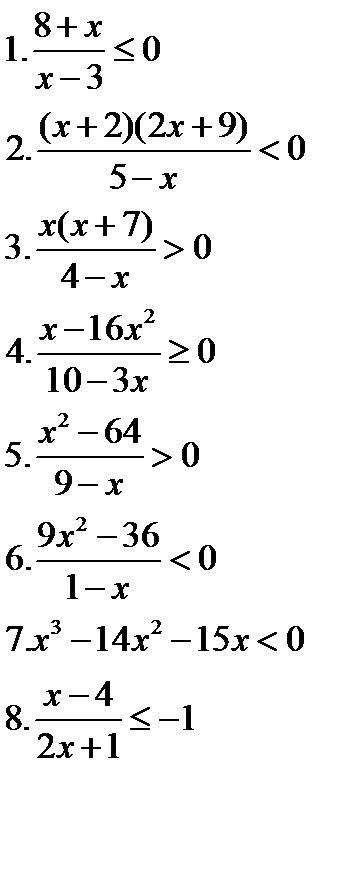 | Решите неравенства 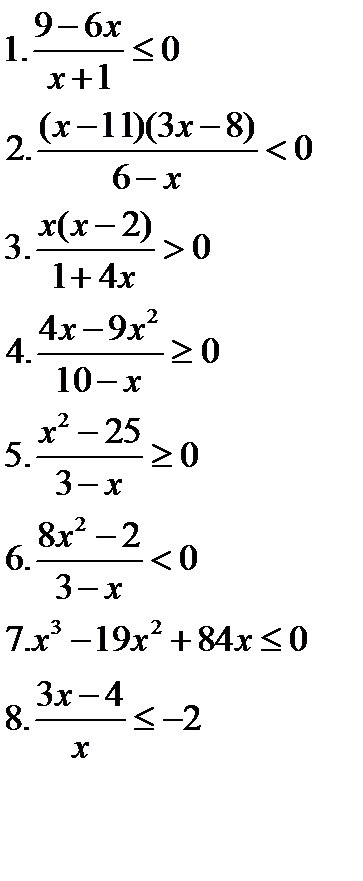 |
| ИЗ-5: Метод интервалов | ИЗ-5: Метод интервалов | ИЗ-5: Метод интервалов | ИЗ-5: Метод интервалов |
| 5 вариант | 6 вариант | 3 вариант | 4 вариант |
Решите неравенства  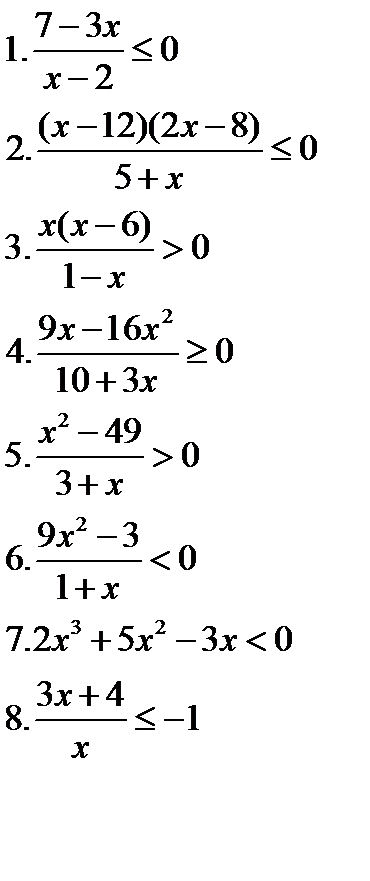 | Решите неравенства 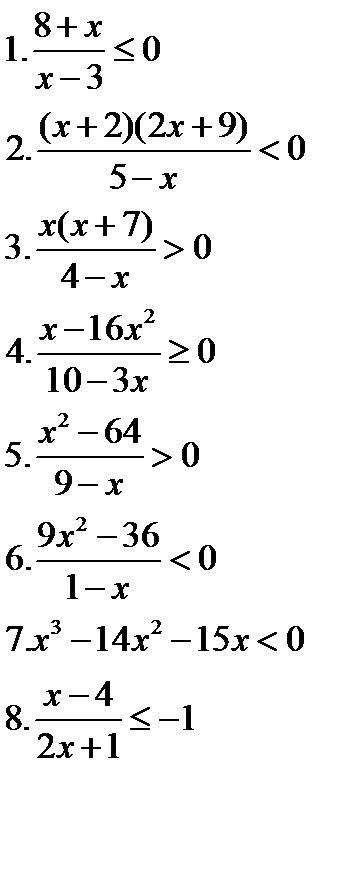 | Решите неравенства 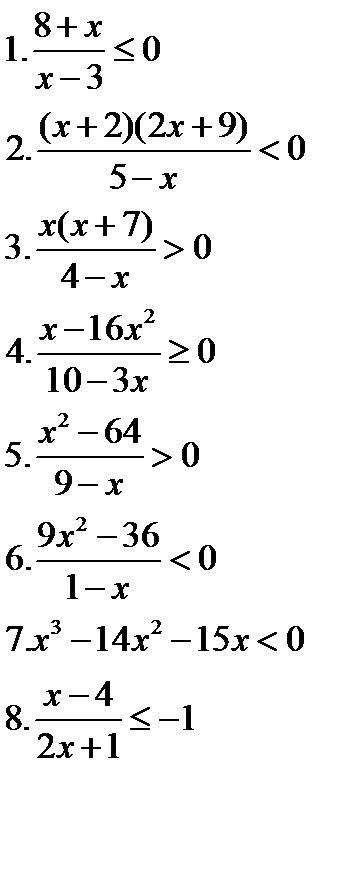 | Решите неравенства 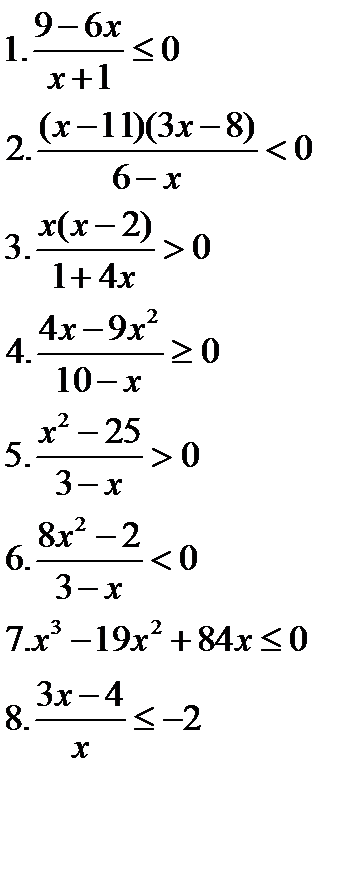 |
