Контрольная работа по эконометрике «Построение парной линейной регрессии».

4.1 Задание:

Исходные данные(см. Приложение 1)представляют собой двумерную выборку 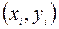, 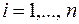. По выборке необходимо построить парную линейную регрессию и оценить качество построенной модели.

4.2 Порядок выполнения работы:

1. Для заданных исходных данных постройте поле корреляции — диаграмму зависимости показателя от фактора . При построении выберите тип диаграммы «Точечная» (без отрезков, соединяющих точки).

Вычислите коэффициенты выборочной линейной регрессии вручную.

2. Запишите найденное уравнение эмпирической регрессии. Дайте интерпретацию коэффициенту 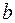в рамках Вашей задачи. Вычислите по уравнению эмпирической регрессии значения , .

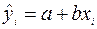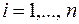3. Постройте на корреляционном поле прямую выборочной линейной регрессии по точкам 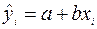, 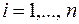. (При построении выберите тип диаграммы «Точечная», на которой значения соединены отрезками.)

4. Найдите величину средней ошибки аппроксимации 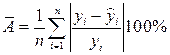. Прокомментируйте полученное значение.

5. Вычислите коэффициент детерминации 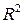непосредственно по формуле:

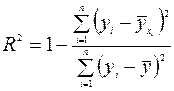
6. Используя построенную модель, рассчитайте значение зависимой переменной 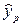при значении фактора 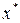,на 10% превышающего среднее значение .

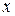7. На основании проведенного выше анализа адекватности модели сделайте вывод о правдоподобности прогноза.

8. Используя опцию Excel «Добавить линию тренда», проверьте свои вычисления и построение графика прямой регрессии.

4.3 Требования к оформлению контрольной работы. Выбор варианта.

Задания могут выполняться с применением компьютера. Вычисления произ­водятся с точностью до двух знаков после запятой.

При выполнении контрольной работы необходимо придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.

1. Студент должен выполнять контрольные задания по варианту, номер которого совпадает с первой буквой его фамилии. Контрольные работы, выполненные не по своему варианту, НЕ ЗАСЧИТЫВАЮТСЯ.

2. Работа сдается на бумажном носителе в печатном виде. Образец оформления работы дан в Приложении 2 настоящих методических указаний.

Приложение 1. Варианты заданий.

Вариант №1 (студенты фамилия которых начинается на А)

В таблице представлены статистические данные о размере товарооборота Х и суммы издержек обращения Y по десяти магазинам.

Товарооборот Х
Издержки обращения Y

Вариант №2 (студенты фамилия которых начинается на Б, В)

Образцы некоторого сплава были изготовлены при различных температурах, после чего была измерена прочность каждого образца. Обозначим через Х температуру изготовления сплава, через Y – величину прочности образца. В таблице приведены результаты измерений.

Х	0,5	1,0	1,5	2,0	2,5	3,0	3,5	4,0	4,5	5,0
Y

Вариант №3 (студенты фамилия которых начинается на Г, Д)

Обозначим через Х цену оптовой продажи некоторого товара, через Y—цену его розничной продажи.

Х

Y

Вариант №4 (студенты фамилия которых начинается на З, К)

Таблица содержит данные о росте (Х) и массе (Y) 25 выбранных наугад студентов.

Х

Y

Вариант №5 (студенты фамилия которых начинается на М, Н)

Х	6,7	6,9	7,2	7,3	8,4	8,8	9,1	9,8	10,6	10,7	11,1	11,8	12,1	12,4
Y	2,8	2,2	3,0	3,5	3,2	3,7	4,0	4,8	6,0	5,4	5,2	5,4	6,0	9,0

Приведены данные о годовой производительности труда в расчете на одного рабочего (Y) и энерговооруженности труда (Х) на предприятиях одной отрасли.

Вариант №6 (студенты фамилия которых начинается на П, Р)

На 10 территориях были измерены процентный показатель перенаселенности (Х) и показатель детской смертности (Y).

Х
Y

Вариант №7 (студенты фамилия которых начинается на С, Т)

Х	1,47	1,25	1,82	1,45	1,75	1,37	1,61	1,93	1,68	1,66
Y	34,08	35,89	36,93	32,31	34,91	30,20	31,23	48,13	30,08	42,86

Имеются данные о фондоотдаче оборудования (Х) и удельном весе продукции высшей категории качества (Y):

Вариант №8 (студенты фамилия которых начинается на Х, Ч)

В таблице содержатся данные, показывающие связь между количеством дней (Х), проведенных пациентами в больнице, и затратами больницы (Y), которые компенсируются страховой компанией.

Х

Y

Приложение 2. Образец оформления контрольной работы.

Государственное образовательное учреждение высшего профессионального образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ПРЕПОДАВАТЕЛЬ

должность, уч. степень, звание		подпись, дата		инициалы, фамилия

КОНТРОЛЬНАЯ РАБОТА

по дисциплине: эконометрика

РАБОТУ ВЫПОЛНИЛА

СТУДЕНТ(КА) ГР.
			подпись, дата		инициалы, фамилия

Санкт-Петербург
2010

Задача.

По 21 региону страны изучается зависимость розничной продажи телевизоров ( 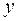) от среднедушевого денежного дохода в месяц ( ).

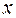Номер региона	Среднедушевой денежный доход в месяц, тыс. руб.,	Объем розничной продажи телевизоров, тыс. шт.,
	2,4	21,3
	2,1
	2,6	23,3
	1,7	15,8
	2,5	21,9
	2,4
	2,6
	2,8	23,9
	2,6
	2,6	24,6
	2,5
	2,9
	2,6
	2,2
	2,6
	3,3	31,9
	3,9
		35,4
	3,7
	3,4

Решение.

1. Построим поле корреляции.

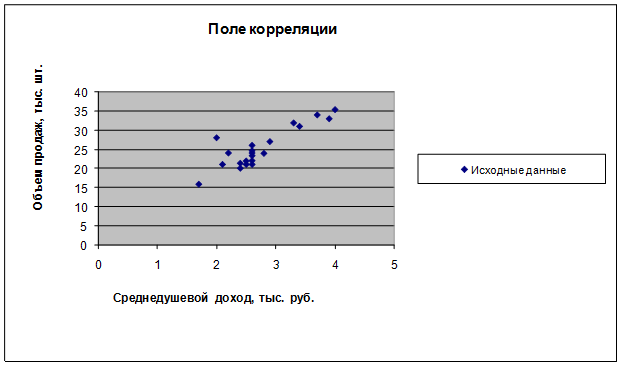
Расположение точек на диаграмме дает нам право предположить, что переменные связаны линейной зависимостью. Рассчитаем выборочные коэффициенты корреляции. Для этого проведем промежуточные вычисления, по формулам ( ) и поместим результаты вычислений в таблицу:

Номер региона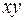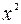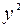
	2,4	21,3	51,12	5,76	453,69
	2,1		44,1	4,41
	2,6	23,3	60,58	6,76	542,89
	1,7	15,8	26,86	2,89	249,64
	2,5	21,9	54,75	6,25	479,61
	2,4			5,76
	2,6		57,2	6,76
	2,8	23,9	66,92	7,84	571,21
	2,6		67,6	6,76
	2,6	24,6	63,96	6,76	605,16
	2,5		52,5	6,25
	2,9		78,3	8,41
	2,6		54,6	6,76
	2,2		52,8	4,84
	2,6		62,4	6,76
	3,3	31,9	105,27	10,89	1017,61
	3,9		128,7	15,21
		35,4	141,6		1253,16
	3,7		125,8	13,69
	3,4		105,4	11,56
Сумма	57,4	530,1	1504,46	164,32	13926,97

Составляем систему уравнений:

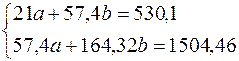
и решаем ее по формулам Крамера:

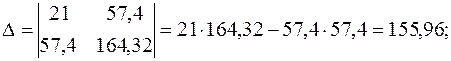
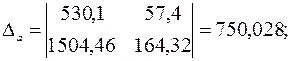
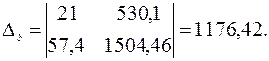
Тогда, согласно теореме Крамера,

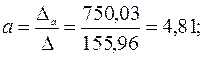
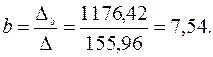
2. Получаем уравнение регрессии:

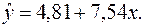
Величина коэффициента регрессии 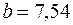означает, что увеличение среднедушевого месячного дохода на 1 тыс. руб. приведет к увеличение объема розничной продажи в среднем на 7 540 телевизоров. Коэффициент 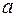в данном случае не имеет содержательной интерпретации.

3. Нанесем построенную линию регрессии на диаграмму. Для этого рассчитаем значения 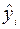, , 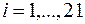по формуле:

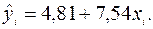
Результаты вычислений запишем в таблицу:

Номер региона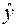
			19,76
	2,4	21,3	22,75
	2,1		20,51
	2,6	23,3	24,25
	1,7	15,8	17,52
	2,5	21,9	23,50
	2,4		22,75
	2,6		24,25
	2,8	23,9	25,74
	2,6		24,25
	2,6	24,6	24,25
	2,5		23,50
	2,9		26,49
	2,6		24,25
	2,2		21,26
	2,6		24,25
	3,3	31,9	29,48
	3,9		33,96
		35,4	34,71
	3,7		32,47
	3,4		30,23

Наносим на диаграмму точки из последнего столбца таблицы (Линия регрессии):

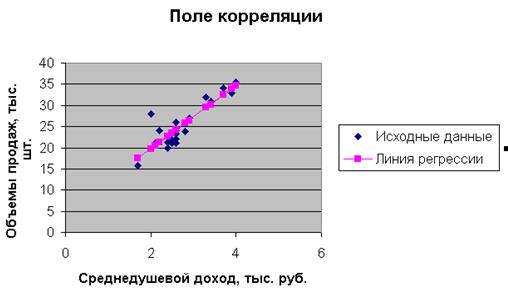
4. Для оценки тесноты линейной зависимости рассчитаем коэффициент детерминации. Для этого необходимо провести ряд дополнительных вычислений.

Прежде всего, найдем выборочное среднее 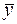по формуле:

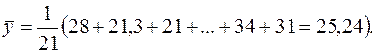
Теперь произведем расчет остальных вспомогательных величин:

Номер региона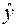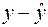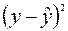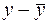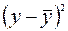
			19,76	8,24	67,89	2,76	7,60
	2,4	21,3	22,75	-1,45	2,11	-3,94	15,55
	2,1		20,51	0,49	0,24	-4,24	18,00
	2,6	23,3	24,25	-0,95	0,90	-1,94	3,77
	1,7	15,8	17,52	-1,72	2,95	-9,44	89,17
	2,5	21,9	23,50	-1,60	2,56	-3,34	11,17
	2,4		22,75	-2,75	7,57	-5,24	27,49
	2,6		24,25	-2,25	5,04	-3,24	10,52
	2,8	23,9	25,74	-1,84	3,39	-1,34	1,80
	2,6		24,25	1,75	3,08	0,76	0,57
	2,6	24,6	24,25	0,35	0,13	-0,64	0,41
	2,5		23,50	-2,50	6,24	-4,24	18,00
	2,9		26,49	0,51	0,26	1,76	3,09
	2,6		24,25	-3,25	10,54	-4,24	18,00
	2,2		21,26	2,74	7,53	-1,24	1,54
	2,6		24,25	-0,25	0,06	-1,24	1,54
	3,3	31,9	29,48	2,42	5,86	6,66	44,32
	3,9		33,96	-0,96	0,93	7,76	60,17
		35,4	34,71	0,69	0,47	10,16	103,17
	3,7		32,47	1,53	2,34	8,76	76,69
	3,4		30,23	0,77	0,60	5,76	33,14
Сумма	57,4	530,1			130,68		545,73

Для вычисления коэффициента детерминации воспользуемся формулой ( ):

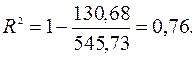
Значение коэффициента детерминации позволяет сделать предварительный вывод о том, что у нас имеются основания использовать модель линейной регрессии в данной задаче, поскольку .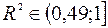

5. Нанесем теперь уравнение регрессии на диаграмму, используя специальные средства Excel («Добавить линию тренда»).

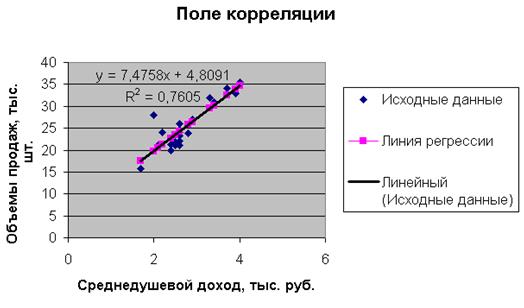
Линия регрессии, построенная нами ранее, совпала с данной линией регрессии. Нетрудно убедиться, что уравнение регрессии и коэффициент детерминации тоже совпадают с полученными ранее вручную.

6. Найдем теперь среднюю ошибку аппроксимации для оценки погрешности модели. Для этого нам потребуется вычислить еще ряд промежуточных величин:

Номер региона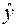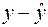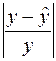
			19,76	8,24	0,29
	2,4	21,3	22,75	-1,45	0,07
	2,1		20,51	0,49	0,02
	2,6	23,3	24,25	-0,95	0,04
	1,7	15,8	17,52	-1,72	0,11
	2,5	21,9	23,50	-1,60	0,07
	2,4		22,75	-2,75	0,14
	2,6		24,25	-2,25	0,10
	2,8	23,9	25,74	-1,84	0,08
	2,6		24,25	1,75	0,07
	2,6	24,6	24,25	0,35	0,01
	2,5		23,50	-2,50	0,12
	2,9		26,49	0,51	0,02
	2,6		24,25	-3,25	0,15
	2,2		21,26	2,74	0,11
	2,6		24,25	-0,25	0,01
	3,3	31,9	29,48	2,42	0,08
	3,9		33,96	-0,97	0,03
		35,4	34,71	0,69	0,02
	3,7		32,47	1,53	0,05
	3,4		30,23	0,77	0,02

Просуммируем теперь элементы последнего столбца и разделим полученную сумму на 21 – общее количество исходных данных:

.

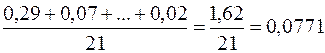Итак, средняя ошибка аппроксимации 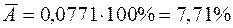. Величина ошибки оказалась около 8%, что говорит о небольшой погрешности построенной модели. Данную модель, с учетом неплохих характеристик ее качества, вполне можно использовать для прогноза – одной из основных целей эконометрического анализа.

7. Рассчитаем значение фактора, для которого необходимо построить прогноз. Для этого необходимо вычислить выборочное среднее значение по формуле:

.

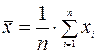Для нашей задачи среднее значение среднедушевого месячного дохода:

.

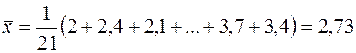Рассчитаем теперь значение .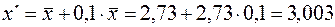

Подставим теперь полученное значение фактора 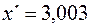в уравнение регрессии и найдем прогнозируемое значение:

.

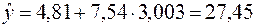Таким образом, если среднедушевой месячный доход в некотором регионе составит 3 003 руб., количество продаваемых телевизоров составит в среднем 27 450 шт. в месяц.