Символьные операции математического анализа

1. Функция вычисления производных – diff

Для вычисления в символьном виде производных от выражения S служит функция diff, записываемая в формате diff(S,'v') или diff(S, sym('v')) Она возвращает символьное значение первой про­изводной от символьного выражения или массива символьных вы­ражений S по переменной v. Эта функция возвращает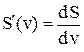

• diff(S, n) — возвращает п-ю (п — целое число) производную символьного выражения или массива символьных выражений Sпо переменной v.

• diff(S, V, n) и diff(S, n, V) – возвращает п-ю производную S по переменной v.

Примеры:

» x =sym( 'x' ); y=sym( 'у' );

» diff(x^y)

ans =

х^у*y / x

» slmplify(ans)

ans =

x^(y-1)*y

» diff(s1n(y*x), x, 3)

ans =

- cos(y*x)*y^3

» diff([x^3 sin(x) exp(x)], x)

ans =

[ 3*x^2, cos(x), exp(x)]

2. Функция интегрирования – int

Функция int вычисляет неопределенные и определенные интегралы

• int(S) — возвращает символьное значение неопределенного инте­грала от символьного выражения или массива символьных выражений S по переменной, которая автоматически определяется функцией findsym. Если S — скаляр или матрица, то вычисляется интеграл по переменной 'х'.

• int(S, v) — возвращает неопределенный интеграл от S по перемен­ной v .

• int(S, a, b) — возвращает определенный интеграл от S с пределами интегрирования от а до b, причем пределы интегрирования могут быть как символьными, так и числовыми.

• int(S, v, a, b) — возвращает определенный интеграл от S по пере­менной v с пределами от а до b.

Примеры:

» int(sin(x)^3, x)

ans =

- l/3*sin(x)^2*cos(x)-2/3*cos(x)

» int(log(2*x), x)

ans =

log(2*x)*x - x

» int((x^2-2)/(x*3-l), x, l, 2)

ans =

-inf

» int((x^2-2)/(x*3-l), x, 2, 5)

ans =

- 2/3*1og(2) + 2/3*1og(31) + 2/3*3^(l/2)*atan(11/3*3^(l/2)) -...

2/3*log(7) - 2/3*3^(1/2)*atan(5/3*3^(l/2))

» int([x^3 sin(x) exp(x)], x)

ans =

[ l/4*x^4, -cos(x), exp(x)]

» int(log(sin(x)),x,0,pi/2)

ans =

-pi/2*log(2)

С помощью функции int можно вычислять имеющие аналитическое решение сложные интегралы, например с бесконечными пределами (или одним из пределов), а также кратные интегралы.

» int(log(1+exp(-x),x,0,inf)

ans =

pi^2/12

» syms x a b

» int(int(int(x^2 + y^2)*z, x, 0, a), y, 0, a), z, 0, a)

ans =

1/3*a^6

3. Функция вычисления пределов – limit

Для вычисления пределов аналитически заданной функции F(x) служит функция limit

▪ limit(F, x, a) – возвращает предел символьного выражения F в точке х = а.

Пример:

»limit(sin(x)/x, x, 0)

ans =

4. Функция разложения в ряд Тейлора – taylor

▪ taylor (f) – возвращает шесть членов ряда Маклорена функции f ;

▪ taylor (f, n, x, a) – возвращает n членов ряда Тейлора в точке х = а ;

▪ taylor (f, n) – возвращает ( n - 1) членов ряда Маклорена функции f ;

▪ taylor (f, a) – возвращает шесть членов ряда Тейлора функции f в точке а.

Примеры:

»x = sym(‘x’)

»taylor(sin(x))

ans =

x – 1/6*x^3 + 1/120*x^5

»taylor(int(sin(x))

ans =

- 1 +1/2*x^2 – 1/24*x^4

5. Функция вычисления суммы рядов – symsum

Для аналитического вычисления суммы ряда служит команда symsum:

• symsum(S) — возвращает символьное значение суммы бесконечно­го ряда по переменной, найденной автоматически с помощью функ­ции findsym;

• symsum(S, v) — возвращает сумму бесконечного ряда по переменной v;

• symsum(S, a, b) и symsum(S, v, a, b) — возвращают конечную сумму ря­да в пределах номеров слагаемых от а до b.

Примеры:

» x = sym(‘x’);

» symsum(x^2)

ans =

1/3*x^3-1/2*x^2+1/6*x

» symsum([x, x^2, x^3], 1, 5)

ans =

[ 15, 55, 225]

6. Функция решение алгебраических уравнений – solve

Для решения систем алгебраических уравнений и одиночных урав­нений служит функция solve:

• solve(expr1, expr2,... exprN, var1, var2,... varN) — возвращает значения переменных var1, при которых соблюдаются равенства, заданные выражениями exprI. Если в выражениях не используются знаки равенства, то полагается ехргI = 0;

• solve(expr1, expr2, ..... exprN) — аналогична предшествующей функ­ции, но переменные, по которым ищется решение, определяются функцией findsym.

Примеры решения уравнений:

» syms x у;

» so1ve(x^3 -1, x)

ans =

[ 1]

[ -1/2+1/2*i*3^(1/2)]

[ -1/2-1/2*i*3^(1/2)]

» syms a b с

» solve(a*x^2+b*x+c)

ans =

[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))]

[ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]

»S = solve(‘x+y=3’, ‘x*y^2=4’, x, y)

S =

x : [ 3x1 sym ]

y : [ 3x1 sym ]

» S.x

ans =

[4]

[1]

[1]

» S.y

ans =

[-1]

[2]

[2]

» solve(‘sin(x)=0.5’, x)

ans =

0.52359877559829887307710723054658

7. Решение дифференциальных уравнений – dsolve

Для решения дифференциальных уравнений в форме Коши MATLAB имеет следующую функцию:

• dsolve( 'eqn1', 'eqn2', ...) — возвращает аналитическое решение сис­темы дифференциальных уравнений с начальными условиями. Они задаются равенствами eqnl (вначале задаются уравнения, затем начальные условия).

По умолчанию независимой переменной считается переменная 't', обычно обозначающая время. Можно использовать и другую пере­менную, добавив ее в конец списка параметров функции dsolve. Сим­вол D обозначает производную по независимой переменной, то есть d / dt, при этом D2 означает d² / dt² и т. д. Имя независимой перемен­ной не должно начинаться с буквы D.

Начальные условия задаются в виде равенств 'у(а)=b' или 'Dy(a)=b', где у — независимая переменная, а и b — константы. Если число на­чальных условий меньше, чем число дифференциальных уравнений, то в решении будут присутствовать произвольные постоянные С1, С2 и т. д.

Примеры применения функции dsolve:

» dsolve('D2x = -2*x')

ans =

Cl*cos(2^(1/2)*t) + C2*sin(2^(l/2)*t)

» dsolve('D2y = -2*x + y', 'у(0) = 1 , 'х')

ans =

(2*х*ехр(х) + (- С2 + 1)*ехр(х)^2 + С2 / ехр(х)