Логарифмическое дифференцирование

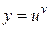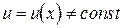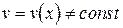Показательно-степенной функцией называется функция вида , где , – дифференцируемые функции и .

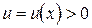Для нахождения производной такой функции ее сначала логарифмируют, а затем дифференцируют полученное равенство.

Логарифмическое дифференцирование применяется также для функций, состоящих из большого числа сомножителей или являющихся отношением произведений нескольких функций.

Примеры.

1. Найти производную функции .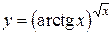

.

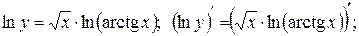
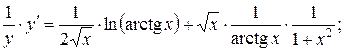
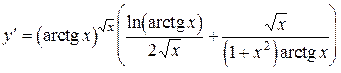2. Найти производную функции .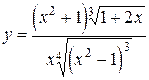

;

;

.

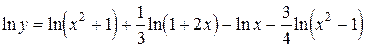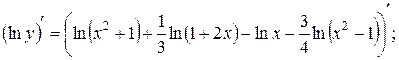
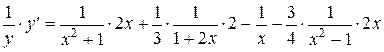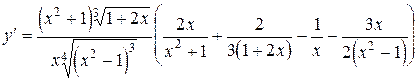Замечание. При решении применялись следующие свойства логарифмов:

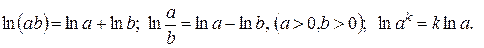
Дифференциал

К графику непрерывной функции 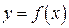в точке 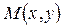проведем касательную MT, обозначив через j ее угол наклона к положительному направлению оси Ох. Так как 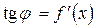, то из треугольника MEF следует, что .

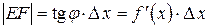Введем обозначение .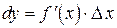

Это выражение называется дифференциалом функции 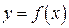. Итак .

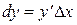Замечая, что 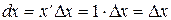, т.е. что дифференциал независимой переменной равен ее приращению, получим

.

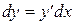Таким образом, дифференциал функции равен произведению ее производной на дифференциал (или приращение) независимой переменной.

Из последней формулы следует, что 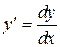, т.е. производная функции равна отношению дифференциала этой функции к дифференциалу аргумента.

Дифференциал функции dy геометрически представляет собой приращение ординаты касательной, соответствующее приращению аргумента Dх.

Из рисунка видно, что при достаточно малом Dх по абсолютной величине можно взять приращение функции 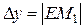приближенно равным ее дифференциалу, т.е.

.

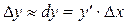Все правила дифференцирования можно записать для дифференциалов.

Пусть 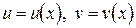– дифференцируемы в точке х. Тогда

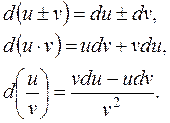
Дифференцирование функций, заданных параметрически

Для нахождения производной функции, заданной параметрически

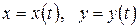, где 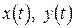– известные дифференцируемые функции параметра 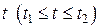, воспользуемся тем, что 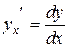. Тогда

.

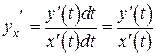Таким образом, производная параметрически заданной функции равна отношению частных производных переменных и 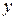по параметру .

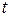Пример. .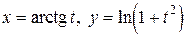

.

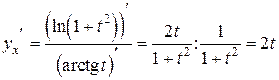Производная неявной функции

Пусть дано уравнение вида 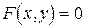, связывающее переменные и 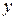. Если 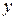нельзя явно выразить через , (разрешить относительно 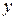) то такая функция называется неявно заданной. Чтобы найти производную от такой функции, нужно обе части уравнения продифференцировать по , считая 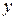функцией от . Из полученного нового уравнения найти .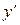

Пример. .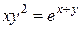

Дифференцируем обе части уравнения по , помня, что 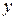есть функция от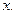

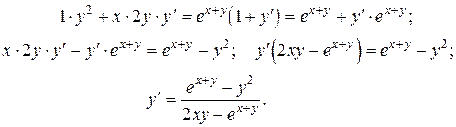
Пример решения работы

Задание №10.Найти пределы функций, не пользуясь правилом Лопиталя:

а) ;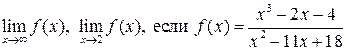
б) 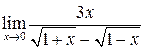;	в) 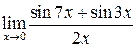;	г) .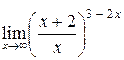

Решение

а) Предел 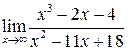содержит неопределенность 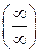. Для того, чтобы раскрыть эту неопределенность, следует разделить числитель и знаменатель на 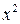− значение переменной в наибольшей степени знаменателя. Тогда

.

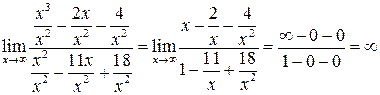Предел 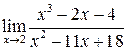содержит неопределенность 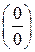. Для того, чтобы раскрыть эту неопределенность, следует преобразовать числитель и знаменатель, разложив их на множители. Разделим числитель и знаменатель на 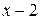, то есть на тот множитель, который обращает их в 0.

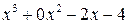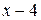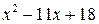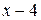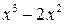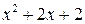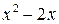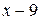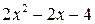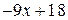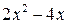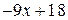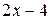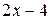Тогда:

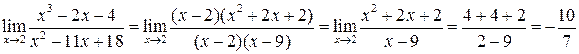
б) Предел 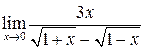содержит неопределенность вида 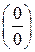. Для этого, чтобы раскрыть эту неопределенность, следует знаменатель и числитель умножить на сопряженный многочлен знаменателя :

.

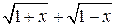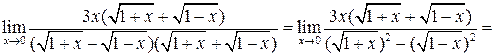
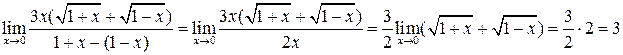в) Предел 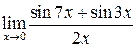содержит неопределенность вида 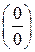. Для раскрытия этой неопределенности преобразуем сумму синусов, стоящих в числителе, в произведение:

,

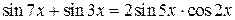получим

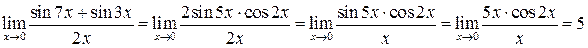
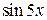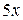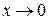(заменим на эквивалентную бесконечно малую при , а ).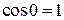

г) При вычислении предела 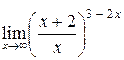имеем дело с неопределенностью ( 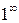). Преобразуем выражение в скобках, выделим 1 и бесконечно малую функцию:

.

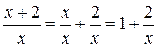Итак,

.

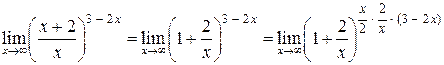Так как при 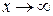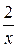− бесконечно малая величина, то .

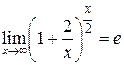Поскольку 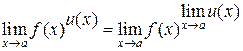, получаем:

.

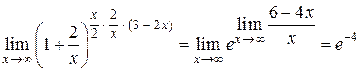Ответ: а) 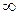; ; 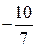б) 3; в) 5; г) .

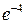Задание №11. Задана функция 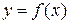. Найти точки разрыва функции, если они существуют. Сделать чертеж.

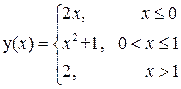
Решение

Очевидно, исследованию подлежат точк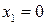и и 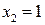, так как в остальных точках числовой оси данная функция 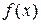непрерывна (представлена непрерывными на всей числовой оси функциям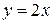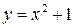и , и .

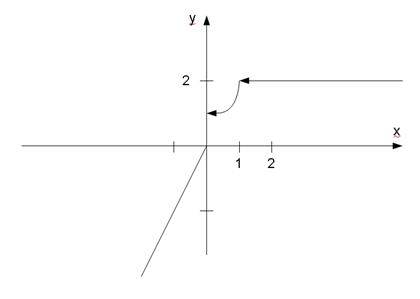
1) 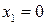. Найдем односторонние пределы:

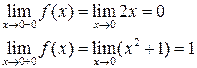
Так как предел функции слева не равен пределу справа, но эти пределы конечны, то в точке 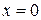данная функция терпит разрыв I рода.

2)

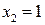
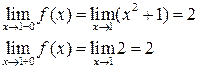
Так как 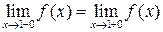, то 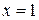− точка непрерывности данной функции .

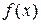График функции представлен на рисунке.

Задание №12. а) Дана функция 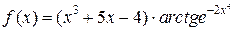. Найти .

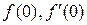б) Найти производные 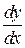данных функций:

1) ;

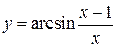2) ;

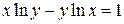3) .

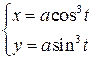Решение

а) Очевидно, что .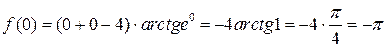

Чтобы найти 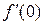найдем сначала 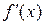. По правилу дифференцирования произведения двух функций и по правилу дифференцирования сложной функции имеем:

.

.

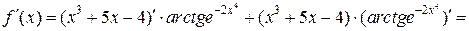
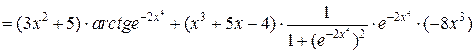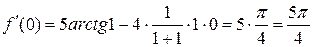б) 1) .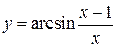

По правилу дифференцирования сложной функции:

.

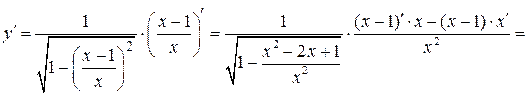
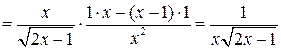2)

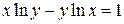
Это неявно заданная функция. Найдем производные обеих частей данного равенства. Не забудем при этом, что .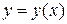

.

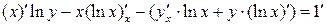
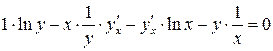
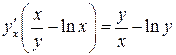
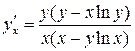3)

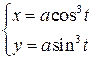
В этом случае функция задана параметрическим способом. Производная от такой функции находится по формуле:

.

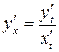Найдем 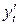и :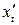

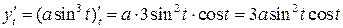
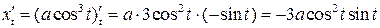
Но тогда

.

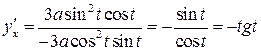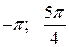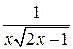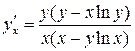Ответ: а) . б) 1) ; 2) ; 3) .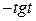

Задание №13. Показать, что функция 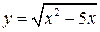удовлетворяет уравнению

.

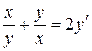Решение

Найдем :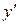

.

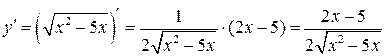Левая часть данного уравнения при 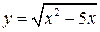примет вид:

;

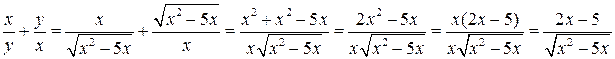Правая часть:

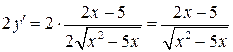, что и требовалось установить.

Раздел 4. Задания для самостоятельного выполнения

Контрольная работа №1