Вычисление пределов в точке.
1)Предел многочлена. Для вычисления пределов многочлена f(х) = р(х) = ахп + вхп – 1 +… + с при х→а достаточно вместо переменной х подставить значение а, к которому она стремится, и выполнить соответствующие действия.
Пример3. Вычислить  Решение: Применим Теорему 1
Решение: Применим Теорему 1
 ) = 49
) = 49
2)Предел отношения двух многочленов 
а) если g(a) ≠ 0, то можно применить теорему о пределе частного.
Пример 4: Вычислить  =
=  .
.
б) если g(a) = 0, то теорему о пределе частного применить нельзя. Тогда если f(а) = А ≠ 0, то  = ∞.
= ∞.
Пример 5: 
в) если g(a) = 0 и f(а) = 0, то имеем неопределённость вида  . В этом случае предел
. В этом случае предел  можно вычислить разложением многочленов g(х) и f(х) на множители или заменой у = х – а.
можно вычислить разложением многочленов g(х) и f(х) на множители или заменой у = х – а.
Пример 6:
Вычислить  = (
= (  ) =
) =  =
=  =
=  или, заменяя у = х – 2 т.е. х = у + 2 и учитывая, что у→0 при х→2, получаем
или, заменяя у = х – 2 т.е. х = у + 2 и учитывая, что у→0 при х→2, получаем

 =
= 
 .
.
г) Если функция f(x) или g(x) содержит иррациональное выражение, в этом случае для вычисления предела, надо числитель и знаменатель умножить на выражение, сопряжённому корню.
Пример 7:
 =
=  =
=  =
=  =
=  =
=  = -
= - 
д) Если функция f(x) и g(x) содержит иррациональное выражение, в этом случае для вычисления предела, надо числитель и знаменатель умножить на выражение, сопряжённому корню числителя и знаменателя.
Пример 8:

Вычисление пределов в бесконечности. 
д) Если функция f(х) = ахn + bxn – 1 + … + c, то надо вынести за скобки хn, т.о. 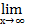 f(x) =
f(x) =  ахn + bxn – 1 + … + c) =
ахn + bxn – 1 + … + c) =  , тогда
, тогда  является бесконечно малой и стремится к 0.
является бесконечно малой и стремится к 0.
Пример 9: 
е) Если функция f(х) =  , где P(x) и Q(x) – многочлены n – степени, то при х →∞ числитель и знаменатель – величины бесконечно большие, поэтому получаем неопределённость вида
, где P(x) и Q(x) – многочлены n – степени, то при х →∞ числитель и знаменатель – величины бесконечно большие, поэтому получаем неопределённость вида  . Чтобы вычислить предел этой функции, надо числитель и знаменатель разделить на старшую степень знаменателя.
. Чтобы вычислить предел этой функции, надо числитель и знаменатель разделить на старшую степень знаменателя.
Пример 10:  = 0,6
= 0,6
Пример 11: 
Пример 12: 
Замечательные пределы.
I замечательный предел: 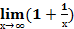 х= е;
х= е; 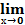
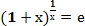 , е = 2,7182818…
, е = 2,7182818…
Пример 13: 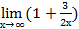 5х =
5х = 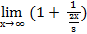 2х/3*3/2*5 =
2х/3*3/2*5 = 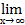 ((1 +
((1 +  )(3х/3))15/2 =
)(3х/3))15/2 =
( Заменим 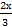 = у и учтём, что у→∞ при х→∞) =
= у и учтём, что у→∞ при х→∞) = 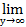 ((1 +
((1 +  )у)15/2 = е15/2
)у)15/2 = е15/2
II замечательный предел: : 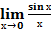 =1;
=1; 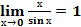 ;
; 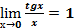
Пример 14: 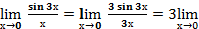
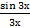 = (заменим 3х = у и учтём, что у→0 при х→0) = 3
= (заменим 3х = у и учтём, что у→0 при х→0) = 3 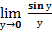 =3*1 = 3
=3*1 = 3
Пример 12: 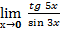 = ( применим формулу
= ( применим формулу 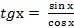 ) =
) = 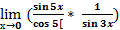 =
= 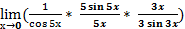 =
= 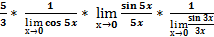 =
= 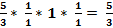
У п р а ж н е н и я д л я с а м о п р о в е р к и:
Вычислите:
1. 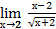 6.
6. 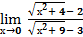
2. 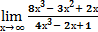 7.
7. 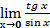
3. 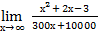 8.
8. 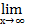
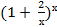
4. 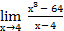 9.
9. 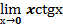
5. 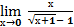 10.
10. 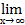
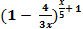
Ответы:1. 0; 2.2; 3.∞; 4.48; 5. 32; 6.1,5; 7.1; 8. 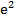 ; 9.1; 10.
; 9.1; 10. 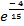 .
.
Дифференциальное исчисление
По данной теме ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Выполните упражнения для самопроверки.
Производная и ее приложения
Производная. Понятие производной является одним из фундаментальных понятий к математике. Многие задачи как самой математики, так и естествознания и техники приводят к этому понятию.
Пусть функция 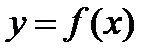 определена в промежутке
определена в промежутке 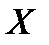 . Возьмем из этого промежутка фиксированное значение аргумента x и придадим ему приращение
. Возьмем из этого промежутка фиксированное значение аргумента x и придадим ему приращение 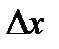 так, чтобы новое значение аргумента
так, чтобы новое значение аргумента 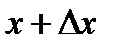 принадлежало этому промежутку. Тогда значение функции
принадлежало этому промежутку. Тогда значение функции 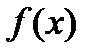 заменится новым значением
заменится новым значением 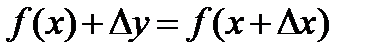 , т.е. функция получит приращение
, т.е. функция получит приращение 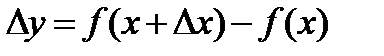 .
.
Предел отношения приращения функции 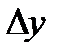 к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента 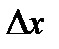 при стремлении
при стремлении 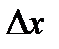 к нулю, т.е.
к нулю, т.е.
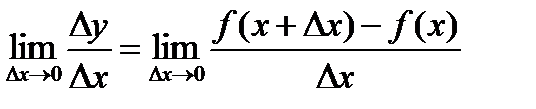 ,
,
называется производной функции 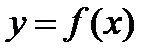 по аргументу x в точке x.
по аргументу x в точке x.
Производная обозначается одним из символов: 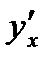 ,
, 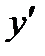 ,
, 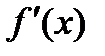 , а ее значение при
, а ее значение при 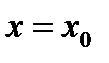 обозначается
обозначается 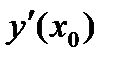 ,
, 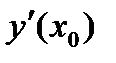 ,
, 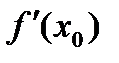 .
.
Операция нахождения производной называется дифференцированием.
Если функция 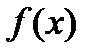 имеет производную в точке x, то она называется дифференцируемой в этой точке.
имеет производную в точке x, то она называется дифференцируемой в этой точке.
Если функция 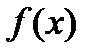 имеет производную в каждой точке промежутка X, то говорят, что эта функция дифференцируема на этом промежутке.
имеет производную в каждой точке промежутка X, то говорят, что эта функция дифференцируема на этом промежутке.
Производная сложной функции. Пусть 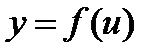 , где u является не независимой переменной, а функцией независимой переменной x:
, где u является не независимой переменной, а функцией независимой переменной x: 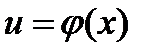 . Таким образом,
. Таким образом, 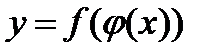 .
.
В этом случае функция y называется сложной функцией x, а переменная u – промежуточным аргументом.
Производная сложной функции находится на основании следующей теоремы: если 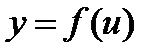 и
и 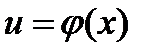 - дифференцируемые функции своих аргументов, то производная сложной функции
- дифференцируемые функции своих аргументов, то производная сложной функции 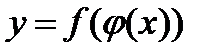 существует и равна произведению производной функции y по промежуточному аргументу и на производной промежуточного аргумента и по независимой переменной x:
существует и равна произведению производной функции y по промежуточному аргументу и на производной промежуточного аргумента и по независимой переменной x:
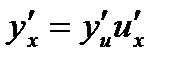 .
.
Эта теорема распространяется и на сложные функции, которые задаются с помощью цепочки, содержащей три звена и более.
Например, если 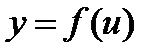 ,
, 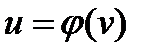 ,
, 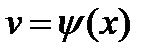 , т.е.
, т.е. 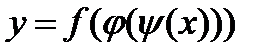 , то
, то 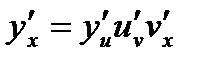 .
.
Формулы дифференцирования.
Правила дифференцирования. Во всех приведенных ниже формулах буквами u и v обозначены дифференцируемые функции независимой переменной x: 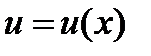 ,
, 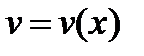 , а буквами a, c, n – постоянные:
, а буквами a, c, n – постоянные:
1. 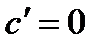
2. 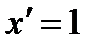
3. 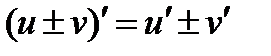
4. 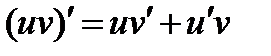
5. 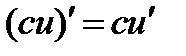
6. 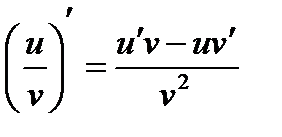
Остальные формулы записаны как для функций независимой переменной, так и для сложных функций:
7. 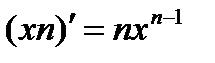
8. 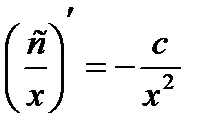
9. 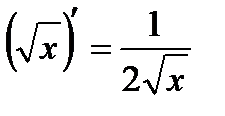
10. 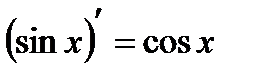
11. 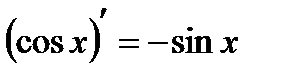
12. 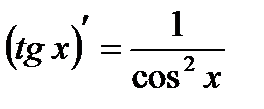
13. 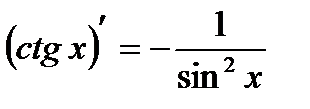
14. 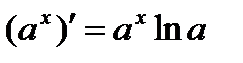
15. 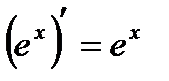
16. 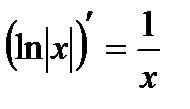
17. 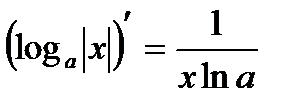
7а. 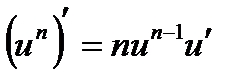
8а. 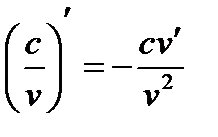
9а. 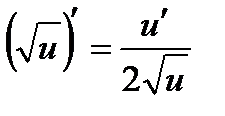
10а. 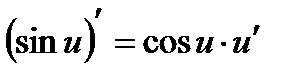
11а. 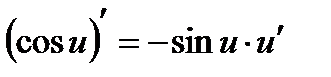
12а. 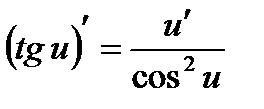
13а. 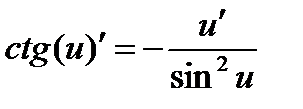
14а. 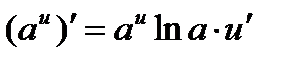
15а. 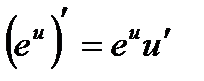
16а. 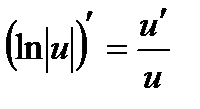
17а. 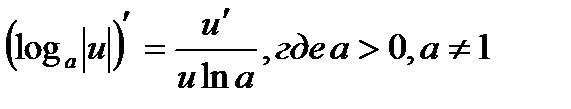
При решении приведенных ниже примеров сделаны подробные записи. Однако следует научиться дифференцировать без промежуточных записей.
Пример 1. Найти производную функции 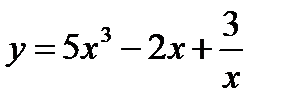 .
.
Решение. Данная функция есть алгебраическая сумма функций. Дифференцируем ее, используя формулы 3, 5, 7 и 8:
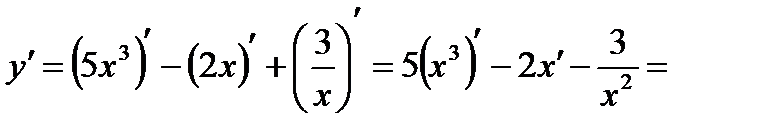
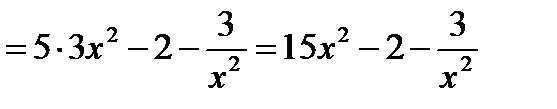
Пример 2. Найти производную функции 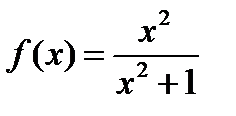
Решение. Применяя формулы 6, 3, 7 и 1, получим
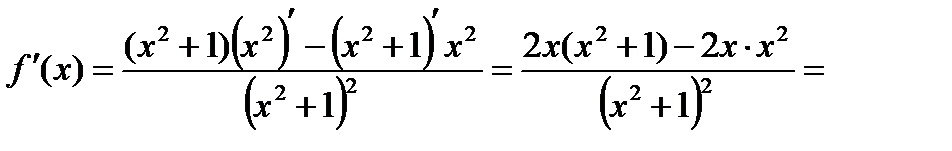
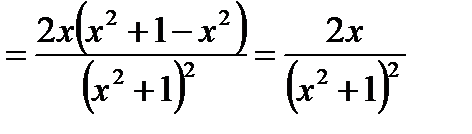
Пример 3. Найти производную функции 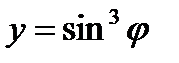 и вычислить ее значение при
и вычислить ее значение при 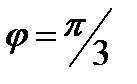
Решение. Это сложная функция с промежуточным аргументом 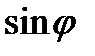 . Используя формулы 7а и 10, имеем
. Используя формулы 7а и 10, имеем
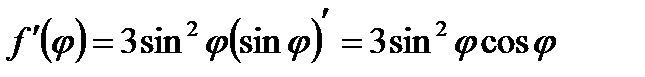 .
.
Вычислим значение производной при 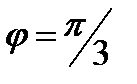 :
:
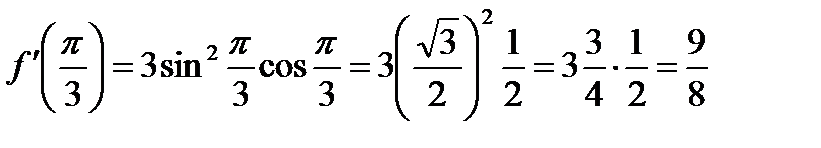 .
.
Пример 4. Найти производную функции 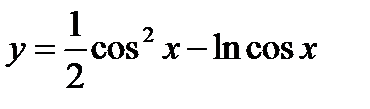 .
.
Решение. Это сложная функция с промежуточным аргументом 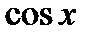 . Применяя формулы 3, 5, 7а, 11, 16а, получим
. Применяя формулы 3, 5, 7а, 11, 16а, получим
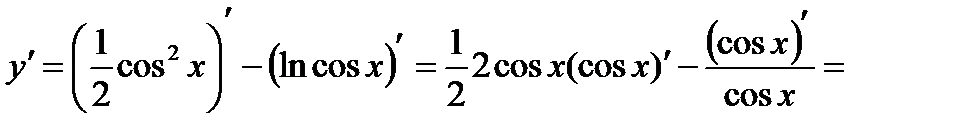
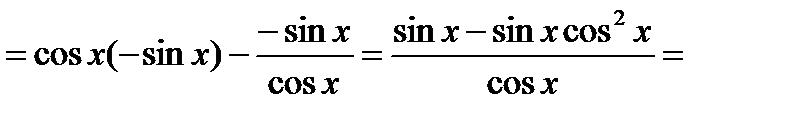
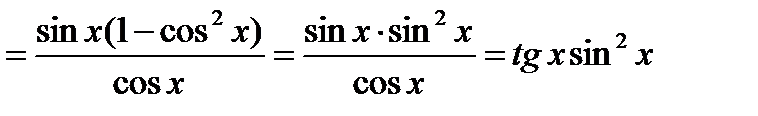
Пример 5. Найти производную функции 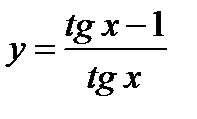 .
.
Решение. Дифференцируем данную функцию по формулам 6, 12, 3 и 1:
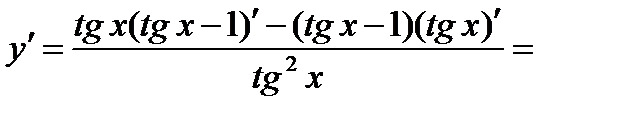
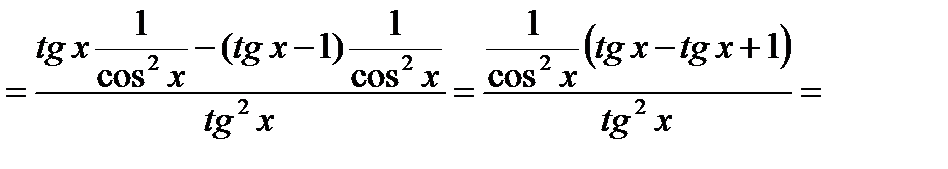
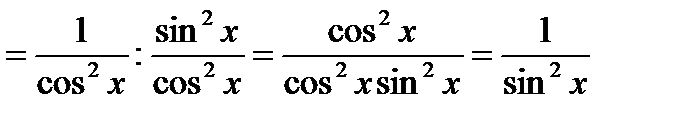
Пример 6. Найти производную функции 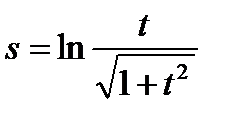 и вычислить ее значение при
и вычислить ее значение при 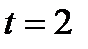 .
.
Решение. Сначала преобразуем функцию, используя свойства логарифмов:
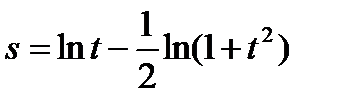
Теперь дифференцируем по формулам 3, 16а, 7 и 1:
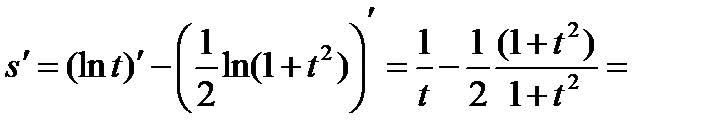
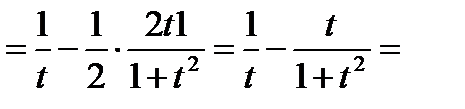
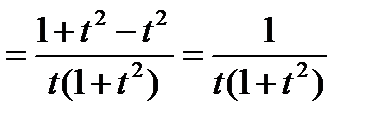 .
.
Вычислим значение производной при 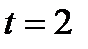 .
.
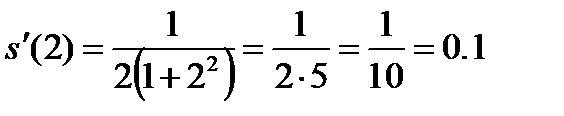
Пример 7. Найти производную функции 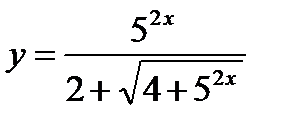 и вычислить ее значение при
и вычислить ее значение при 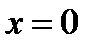 .
.
Решение. Используем формулы 6, 3, 14а, 9а, 5 и 1:
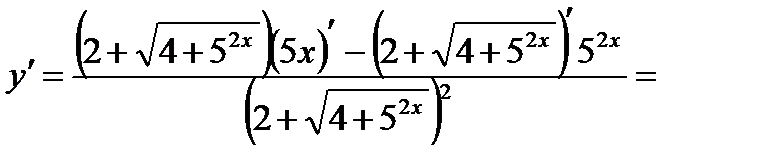
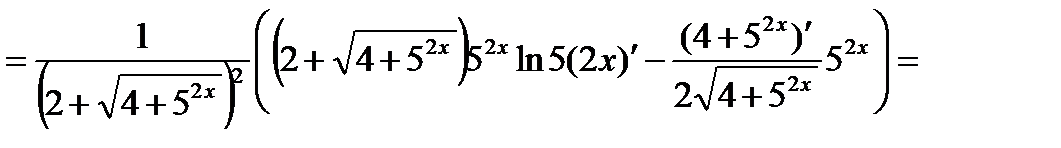
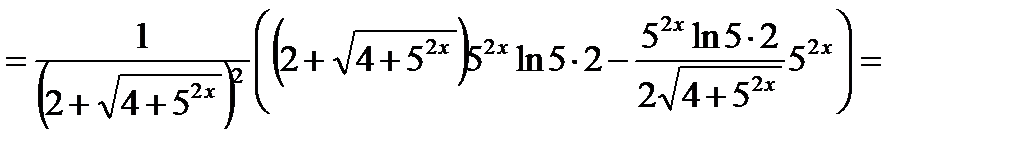
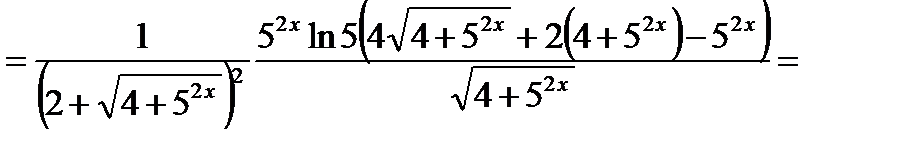
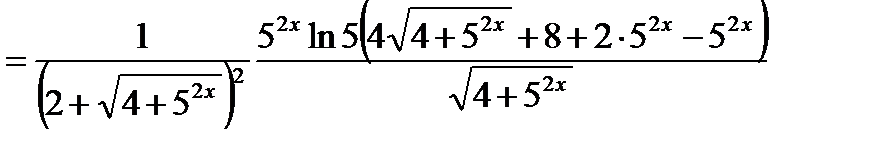
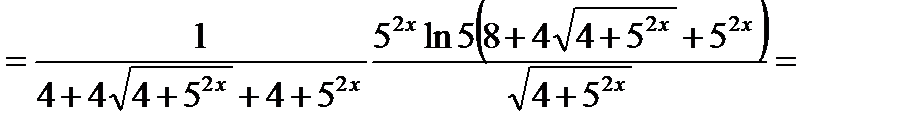
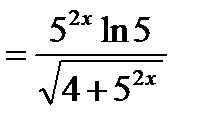 .
.
Вычислим значение производной при 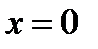 :
:
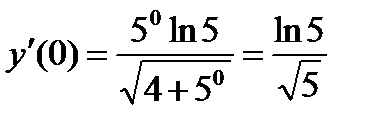 .
.
Геометрический смысл производной.Производная функции имеет простую и важную геометрическую интерпретацию.
Если функция 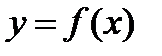 дифференцируема в точке х, то график этой функции имеет в соответствующей точке касательную, причем угловой коэффициент касательной равен значению производной в рассматриваемой точке.
дифференцируема в точке х, то график этой функции имеет в соответствующей точке касательную, причем угловой коэффициент касательной равен значению производной в рассматриваемой точке.
Угловой коэффициент касательной, проведенной к графику функции 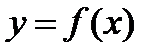 в точке (х0, у0), равен значению производной функции при х=х0, т.е.
в точке (х0, у0), равен значению производной функции при х=х0, т.е. 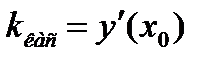 .
.
Уравнение этой касательной имеет вид
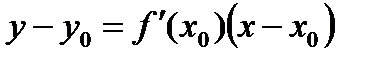 .
.
Пример 8. Составить уравнение касательной к графику функции 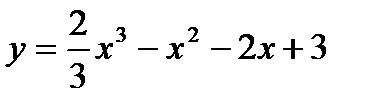 в точке А (3,6).
в точке А (3,6).
Решение. Для нахождения углового коэффициента касательной найдем производную данной функции:
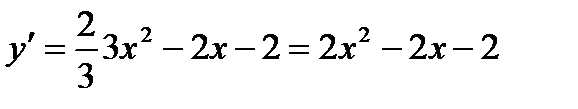 .
.
Угловой коэффициент касательной равен значению производной функции при х=3:
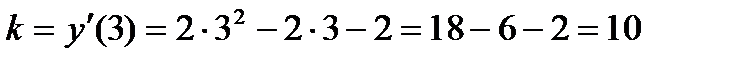 .
.
Уравнение касательной имеет вид
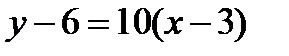 , или
, или 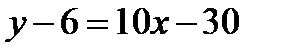 , т.е.
, т.е. 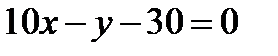
Пример 9. Составить уравнение касательной, проведенной к графику функции 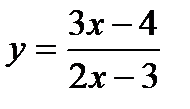 в точке с абсциссой х=2.
в точке с абсциссой х=2.
Решение. Сначала найдем ординату точки касания 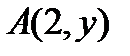 . Так как точка А лежит на кривой, то ее координаты удовлетворяют уравнению кривой, т.е.
. Так как точка А лежит на кривой, то ее координаты удовлетворяют уравнению кривой, т.е.
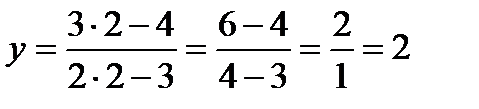 ;
; 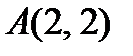 .
.
Уравнение касательной, проведенной к кривой в точке 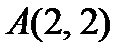 , имеет вид
, имеет вид 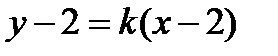 . Для нахождения углового коэффициента касательной найдем производную:
. Для нахождения углового коэффициента касательной найдем производную:
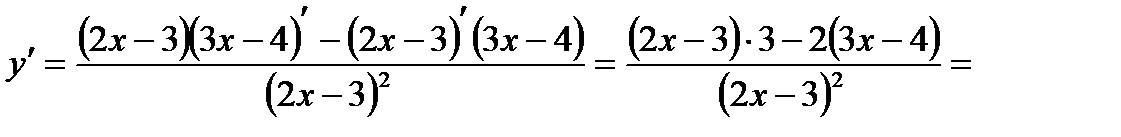
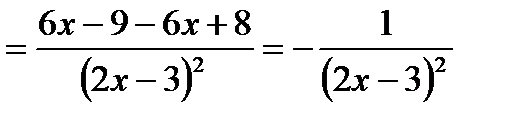 .
.
Угловой коэффициент касательной равен значению производной функции при х=2:
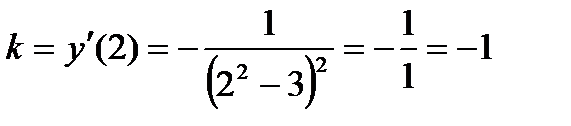
Уравнение касательной таково:
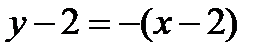 ,
, 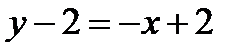 , т.е.
, т.е. 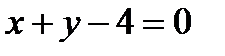
Физический смысл производной. Если тело движется по прямой по закону s=s(t), то за промежуток времени 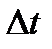 (от момента t до момента
(от момента t до момента 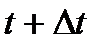 ) оно пройдет некоторый путь
) оно пройдет некоторый путь 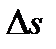 . Тогда
. Тогда 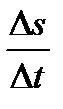 есть средняя скорость движения за промежуток времени
есть средняя скорость движения за промежуток времени 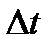 .
.
Скоростью движения тела в данный момент времени t называется предел отношения пути 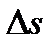 к приращению времени
к приращению времени 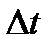 , когда приращение времени стремиться к нулю:
, когда приращение времени стремиться к нулю:
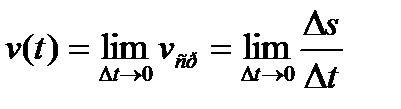 .
.
Следовательно, производная пути s по времени t равна скорости прямолинейного движения тела в данный момент времени:
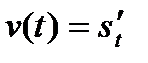 .
.
Скорость протекания физических, химических и других процессов также выражается с помощью производной.
Производная функции 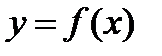 равна скорости изменения этой функции при данном значении аргумента х:
равна скорости изменения этой функции при данном значении аргумента х:
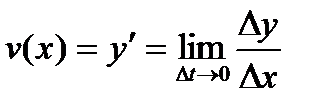
Пример 10.Закон движения точки по прямой задан формулой 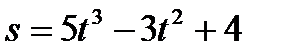 (s – в метрах, t – в секундах). Найти скорость движения точки в конце первой секунды.
(s – в метрах, t – в секундах). Найти скорость движения точки в конце первой секунды.
Решение. Скорость движения точки в данный момент времени равна производной пути s по времени t:
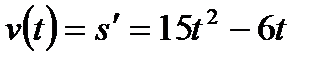 ,
, 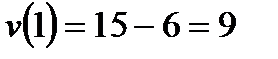
Итак, скорость движения точки в конце первой секунды равна 9 м/с.
Пример 11. Тело, брошенное вертикально вверх, движется по закону 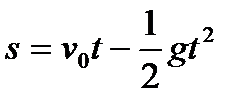 , где v0 – начальная скорость, g –ускорение свободного падения тела. Найти скорость этого движения для любого момента времени t. Сколько времени будет подниматься тело и на какую высоту оно поднимется, если v0=40 м/с?
, где v0 – начальная скорость, g –ускорение свободного падения тела. Найти скорость этого движения для любого момента времени t. Сколько времени будет подниматься тело и на какую высоту оно поднимется, если v0=40 м/с?
Решение. Скорость движения точки в данный момент времени t равна производной пути s по времени t:
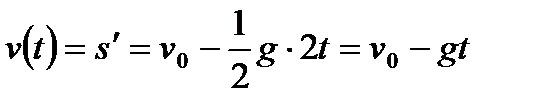 .
.
В высшей точке подъема скорость тела равна нулю:
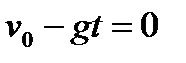 ,
, 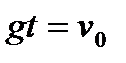 ,
, 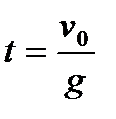 ,
, 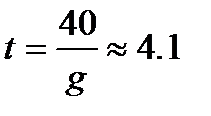 ,
, 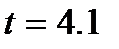 с.
с.
За 40/g секунд тело поднимается на высоту
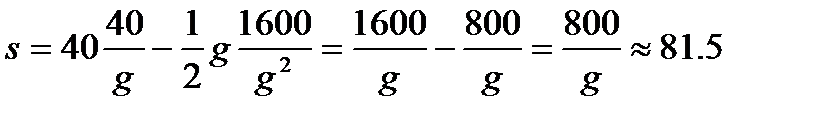 ,
, 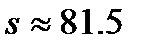 м.
м.
Вторая производная. Производная функции 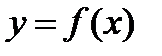 в общем случае является функцией от х. Если от этой функции вычислить производную, то получим производную второго порядка или вторую производную функции
в общем случае является функцией от х. Если от этой функции вычислить производную, то получим производную второго порядка или вторую производную функции 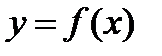 .
.
Второй производной функции 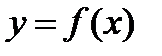 называется производная от ее первой производной
называется производная от ее первой производной 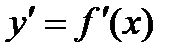 .
.
Вторая производная функции обозначается одним из символов – 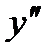 ,
, 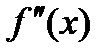 ,
, 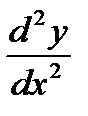 . Таким образом,
. Таким образом, 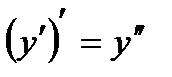 .
.
Аналогично определяются и обозначаются производные любого порядка. Например, производная третьего порядка:
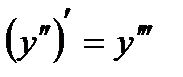 или
или 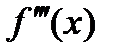 ,
, 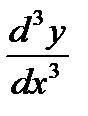
Пример 12.Найти вторую производную функции 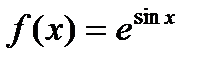 .
.
Решение. Сначала найдем первую производную
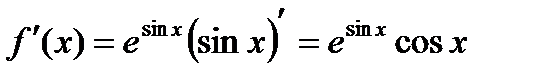
Дифференцируя еще раз, найдем вторую производную:
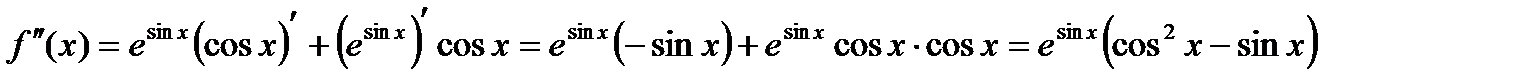 .
.
Пример 13. Найти вторую производную функции 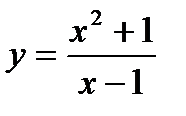 и вычислить ее значение при х=2.
и вычислить ее значение при х=2.
Решение. Сначала найдем первую производную:
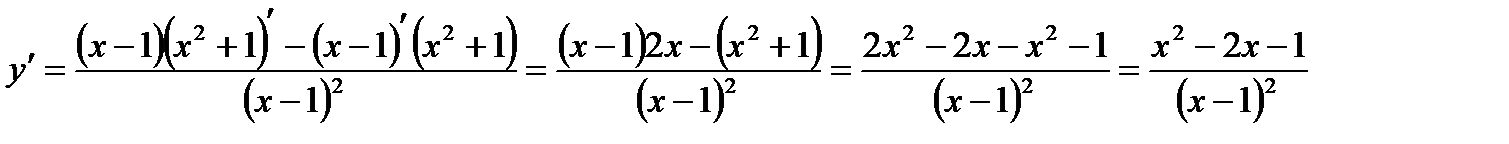
Дифференцируя еще раз, найдем вторую производную:
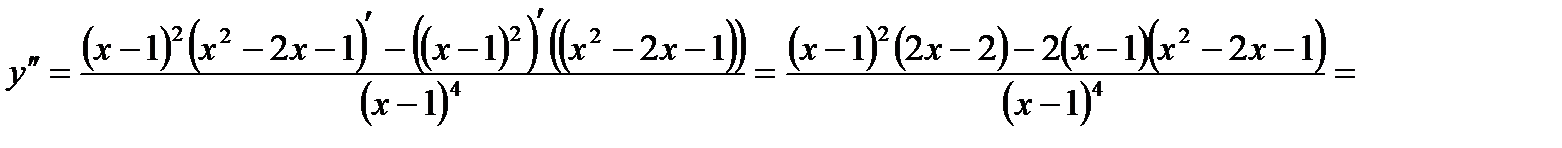
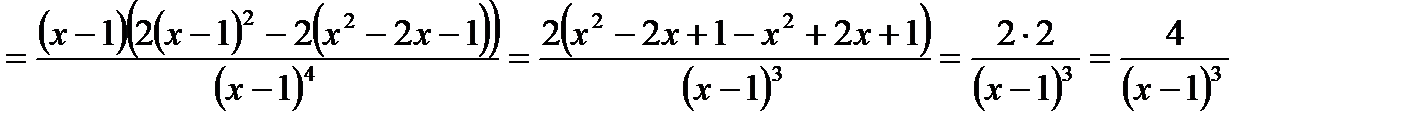 .
.
Вычислим значение второй производной при х=2; имеем 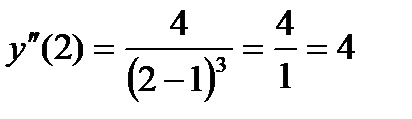
Физический смысл второй производной.Если тело движется прямолинейно по закону s=s(t), то вторая производная пути s по времени t равна ускорению движения тела в данный момент времени t:
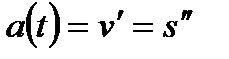
Таким образом, первая производная характеризует скорость некоторого процесса, а вторая производная – ускорение того же процесса.
Пример 14. Точка движется по прямой по закону 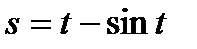 . Найти скорость и ускорение движения
. Найти скорость и ускорение движения 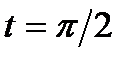 .
.
Решение. Скорость движения тела в данный момент времени равна производной пути s по времени t, а ускорение – второй производной пути s по времени t. Находим:
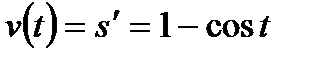 ; тогда
; тогда 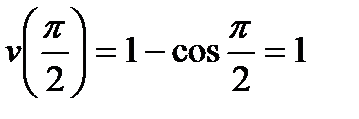 ;
;
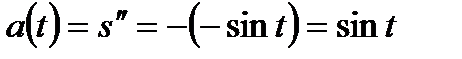 ; тогда
; тогда 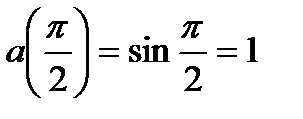
Пример 15.Скорость прямолинейного движения пропорциональна квадратному корню из пройденного пути (как, например, при свободном падении). Доказать, что это движение происходит под действием постоянной силы.
Решение. По закону Ньютона, сила F, вызывающая движение, пропорциональна ускорению, т.е.
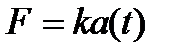 или
или 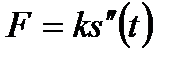
Согласно условию, 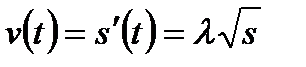 . Дифференцируя это равенство, найдем
. Дифференцируя это равенство, найдем
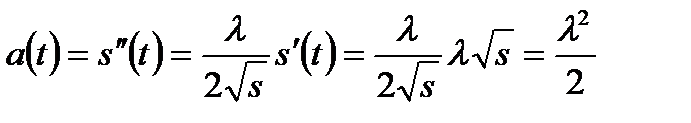
Следовательно, действующая сила 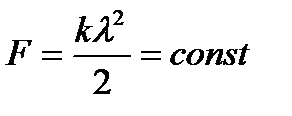 .
.
Приложения производной к исследованию функции.
1) Условие возрастания функции: Дифференцируемая функция y = f(x) монотонно возрастает на промежутке Х тогда и только тогда, когда её производная больше ноля, т. е. y = f(x)↑ f’(x)>0. Это условие геометрически означает, чтокасательная к графику данной функции образует острый угол с положительным направлением к оси оХ.
У
y = f(x)
0 α
Х
2) Условие убывания функции: Дифференцируемая функция y = f(x) монотонно убывает на промежутке Х тогда и только тогда, когда её производная меньше ноля, т. е.
y = f(x)↓  f’(x)<0 .Это условие геометрически означает, чтокасательная к графику данной функции образует тупой угол с положительным направлением оси оХ)
f’(x)<0 .Это условие геометрически означает, чтокасательная к графику данной функции образует тупой угол с положительным направлением оси оХ)
У
α
Х
y = f(x)
3) Условие постоянства функции:Дифференцируемая функция y = f(x) постоянна на промежутке Х тогда и только тогда, когда её производная равна нулю, т. е. y = f(x) – постоянна  f’(x)=0 .Это условие геометрически означает, чтокасательная к графику данной функции параллельна оси оХ, т. е. α = 0)
f’(x)=0 .Это условие геометрически означает, чтокасательная к графику данной функции параллельна оси оХ, т. е. α = 0)
У
0 Х
y = f(x)
Экстремумы функции.
Определение 1: Точку х = х0 называют точкой минимума функции y = f(x), если у этой точки существует окрестность, для всех точек которой (кроме самой точки) выполняется неравенство f(x)> f(x0)
Определение 2: Точку х = х0 называют точкой максимума функции y = f(x), если у этой точки существует окрестность, для всех точек которой (кроме самой точки) выполняется неравенство f(x) < f(x0).
Определение 3: Точку минимума или максимума функции называют точкой экстремума. Значение функции в этой точке называют экстремальным.
Y
Ymax
y = f(x)
x
0 xmin
xmax
Ymin
Замечания: 1. Максимум (минимум) не является обязательно наибольшим (наименьшим) значением функции;
2. Функция может иметь несколько максимумов или минимумо;
3. Функция, определённая на отрезке, может достигать экстремума только во внутренних точках этого отрезка.
5) Необходимое условие экстремума: Если функция y = f(x) имеет экстремум в точке х = х0, то в этой точке производная равна нулю или не существует. Эти точки называются критическими точками 1 рода.
6) Достаточные условия существования экстремума функции: Пусть функция y = f(x) непрерывна на промежутке Х и имеет внутри этого промежуткак ритическую точку 1 рода х = х0, то:
а) если у этой точки существует такая окрестность, в которой при х < х0 f’(x) < 0, а при x> x0 f’(x) > 0, то х = х0 является точкой минимума функции y = f(x);
- + f’(x)
x = x0 f(x)
min
б) если у этой точки существует такая окрестность, в которой при х < х0 f’(x) > 0, а при x> x0
f’(x) < 0, то х = х0 является точкой максимума функции y = f(x);
+ - f’(x)
x = x0 f(x)
max
в) если у этой точки существует такая окрестность, что в ней и справа и слева от точки х0 знаки производной одинаковы, то в точке х0 экстремума нет.
Промежутки убывания или возрастания функции называются промежутками монотонности.
7) Направление выпуклости графика функции. Точки перегиба.
Определение1:Кривая у = f(x) называется выпуклой вниз на промежутке а < х <в, если она лежит выше касательной в любой точке этого промежутка и кривая у = f(x) называется выпуклой вверх на промежутке а < х <в, если она лежит ниже касательной в любой точке этого промежутка.
Определение 2: Промежутки, в которых график функции обращён выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Y
Y = f(x)
0 X
Достаточное условие выпуклости кривой. График дифференцируемой функции Y = f(x) является выпуклым вверх на промежутке а < х <в, если f”(x) < 0 и выпуклым вниз, если f”(x) > 0.
Определение 1: Точки, в которых вторая производная равна нулю или не существует, называются критическими точками II рода.
Определение 2:Точка графика функцииY = f(x), разделяющая промежутки выпуклости противоположенных направлений этого графика, называется точкой перегиб.
+ - f”(x)
х = х0 f(x)
точка перегиба
Пример: Дана функция у = х3 – 2х2 + 6х – 4.Исследовать функцию на промежутки монотонности и точки экстремума. Определить направление выпуклости и точки перегиба.
Решение: 1. Найдем область определения функции: D(y) =  ;
;
2. Найдем первую производную: y’ = 3x2 – 4x + 6;
3. Решим уравнение: y’ = 0, 3x2 – 4x + 6 = 0, D  0, то данное уравнение не имеет решения, следовательно точек экстремуму нет. y’
0, то данное уравнение не имеет решения, следовательно точек экстремуму нет. y’  , то функция возрастает на всей области определения.
, то функция возрастает на всей области определения.
4. Найдем вторую производную:y” = 6x – 4;
5. Решим уравнение: y” = 0, 6x – 4 = 0, х = 
- + y”(x)
 y(x)
y(x)
У(  ) = -
) = - 
Ответ: (  ; -
; -  ) – точка перегиба, функция выпукла вверх при х
) – точка перегиба, функция выпукла вверх при х  и выпукла вверх при х
и выпукла вверх при х 
Асимптоты.
1. Определение: Асимптотой кривой называется прямая, к которой неограниченно приближается график данной функции.
2. Виды асимптот:
1) Вертикальные асимптоты. График функции y = f(x) имеет вертикальную асимптоту, если  . Уравнение вертикальной асимптоты имеет вид х = а
. Уравнение вертикальной асимптоты имеет вид х = а
2) Горизонтальные асимптоты. График функции y = f(x) имеет горизонтальную асимптоту, если  . Уравнение горизонтальной асимптоты имеет вид у = b.
. Уравнение горизонтальной асимптоты имеет вид у = b.
Пример 1: Для функция y =  найдите асимптоты.
найдите асимптоты.
3) Наклонные асимптоты. Прямая y = kx + b называется наклонной асимптотой графика функции y = f(x), если  . Значения k и b вычисляются по формулам: k =
. Значения k и b вычисляются по формулам: k =  ; b =
; b =  .
.
Решение:  , то y = 0 – горизонтальная асимптота;
, то y = 0 – горизонтальная асимптота;
 (т. к. х – 3 ≠ 0, х ≠3), то х = 3 – вертикальная асимптота.
(т. к. х – 3 ≠ 0, х ≠3), то х = 3 – вертикальная асимптота.  ,т. е. k = 0, то кривая наклонной асимптоты не имеет.
,т. е. k = 0, то кривая наклонной асимптоты не имеет.
Пример 2: Для функции y =  найдите асимптоты.
найдите асимптоты.
Решение: x2 – 25 ≠ 0 при x ≠ ± 5, то х = 5 и х = - 5 являются горизонтальными асимптотами;
y =  , то кривая не имеет вертикальной асимптоты;
, то кривая не имеет вертикальной асимптоты;
k =  ; b =
; b =  , т. е. y = 5x – наклонная асимптота.
, т. е. y = 5x – наклонная асимптота.
Примеры построения графиков функций.
Пример 1.
Исследовать функцию и построить график функции у = х3 – 6х2 + 9х – 3
1. Найдём область определения функции: D(y) = R
2. Выясним, является ли данная функция чётной или нечетной:
у( - х) = ( - х)3 - 6·(- х)2 + 9·(-х) – 3 = - х3 – 6х2 – 9х – 3 = - (х3 + 6х2 + 9х + 3), т. е.
у( - х) ≠ у(х) – не является чётной и у( - х) ≠ - у(х) – не является нечётной
( у = х5 – х3 – нечетная, у = х4 + х2 – четная)
3. Не является периодической.
4. Найдем точки пересечения с осями координат: если х = 0, то у = - 3 (0; - 3)
если У = 0, х найти затруднительно.
5. Найдем асимптоты графика функции: Вертикальных асимптот нет, т.к. нет значений х, при которых функция неопределенна; у =  , т. е. горизонтальных асимптот нет;
, т. е. горизонтальных асимптот нет;
k =  , т . е. наклонных асимптот нет.
, т . е. наклонных асимптот нет.
6. Исследуем функцию на промежутки монотонности и её экстремумы: y’ = 3x2 – 12x + 9, y’= 0, 3x2 – 12x + 9 = 0  x1 = 1; x2 = 3 – критические точки 1 рода.
x1 = 1; x2 = 3 – критические точки 1 рода.
+ - + y’(x)
x
1 3 y(x)
max min
ymax = y(1) = 1, (1;1) – точка максимума; ymin = y(3) = - 3, (3; - 3) – точка минимума, функция у↑ при х  и у
и у  .
.
7. Исследуем функцию на промежутки выпуклости и точки перегиба: y” = (y’)’ = (3x2 – 12x + 9)’ = 6x – 12, y” = 0, 6x – 12 = 0  x = 2
x = 2
- + y”(x)
x
2 y(x)
Y(2) = - 1 (2; - 1) – точка перегиба, функция выпукла вверх при х  и выпукла вниз при х
и выпукла вниз при х  .
.
8. Дополнительные точки:
| х | - 1 | |
| у | - 19 |
9. Построим график функции:
У
1
0 1 2 3 4 Х
- 3
- 19
Пример 2.
Исследовать функцию и построить график функции у = 
1. Найдём область определения функции: 1 – х ≠ 0, х ≠ 1, D(y) =  .
.
2. Выясним, является ли данная функция чётной или нечетной:  ,
,
у( - х) ≠ у(х) – не является чётной и у( - х) ≠ - у(х) – не является нечётной
3. Не является периодической.
4. Найдем точки пересечения с осями координат: х = 0, то у = - 2; у = 0,  , то
, то  , т. е. (0; - 2); (
, т. е. (0; - 2); (  ).
).
5. Найдем асимптоты графика функции: т.к. х ≠ 1,то прямая х = 1 – вертикальная асимптота;
у =  , т. е. у = - 3 - горизонтальная асимптота;
, т. е. у = - 3 - горизонтальная асимптота;
k =  , т . е. наклонных асимптот нет.
, т . е. наклонных асимптот нет.
6. Исследуем функцию на промежутки монотонности и её экстремумы: y’ =  =
=  , y’ ≠ 0, т. е. критических точек 1 рода нет, но у’ > 0, то функция возрастает на всей области определения.
, y’ ≠ 0, т. е. критических точек 1 рода нет, но у’ > 0, то функция возрастает на всей области определения.
7. Исследуем функцию на промежутки выпуклости и точки перегиба:
y” = (y’)’ = (  , x ≠ 1
, x ≠ 1
+ - f” (x)
x
1 f(x)
Т. к. х = 1  D(y), то не является точкой перегиба, х = 1 – точка разрыва, функция выпукла вниз при х
D(y), то не является точкой перегиба, х = 1 – точка разрыва, функция выпукла вниз при х  и выпукла вверх при х
и выпукла вверх при х 
8. Дополнительные точки:
| х | - 1 | ||
| у | - 2,5 | - 4 | - 3,5 |
9. Построим график функции:
У
Х = 1

- 1 0 1 2 3 Х
- 2
У = -3
- 3
- 4
Пример 3:
Исследовать функцию и построить график функции у = 
1. Найдём область определения функции: х ≠ 0, D (y) = ( - ∞; 0) U (0; + ∞)
2. Выясним, является ли данная функция чётной или нечетной: y( - x) = -  , y(x) = - y(x) – то функция нечётная и график симметричен относительно начала координат.
, y(x) = - y(x) – то функция нечётная и график симметричен относительно начала координат.
3. Не является периодической.
4. Найдем точки пересечения с осями координат: х ≠ 0, то у ≠ 0, граф
