Исследование на плоскости уравнения второй степени

Рассмотрим уравнение:

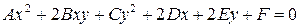(7.9)

где среди коэффициентов 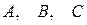есть отличные от нуля, т.е. (7.9) – уравнение второй степени относительно 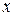и .

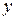Возьмем на плоскости две прямоугольные системы координат: 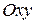, которую будем называть старой, и новую, полученную из 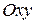поворотом ее вокруг начала координат на угол , .

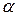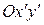Старые координаты 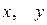выражаются через новые координаты 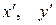по формулам:

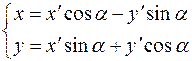(7.10)

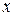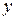Подставив выражения для и в уравнение (8), получим:

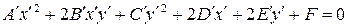(7.11)

Это уравнение в системе координат 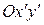задает ту же линию, что и уравнение (7. 9) в системе .

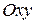Если в уравнении (7.9) 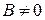, то за счет выбора угла 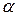в (7.10) можно добиться того, что 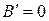. Для этого угол 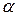надо взять таким, чтобы 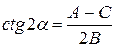. Поэтому будем считать 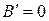, тогда уравнение (7.11) примет вид:

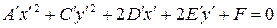(7.12)

Преобразуя это уравнение и применяя параллельный перенос координатных осей, придем к уравнению:

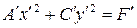(7.13)

В зависимости от знаков коэффициентов уравнения (7.13) рассмотрим следующие случаи:

I. 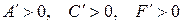, тогда уравнение (7.13) примет вид 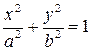, где 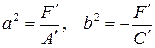. Это уравнение эллипса.

II. 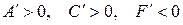, то, обозначив 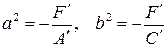,имеем 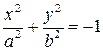. Этому уравнению не удовлетворяет ни одна точка с координатами 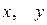. Следовательно, это уравнение задает пустое множество.

III. 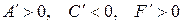. Обозначая 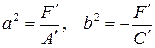приведем уравнение (12) к виду 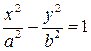. Это уравнение гиперболы.

IV.Случаи 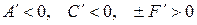, , 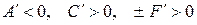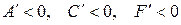новых результатов не дают.

V. 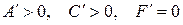. Тогда уравнение (7.13) можно привести к виду 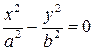. Это уравнение задает пару прямых 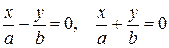, пересекающихся в начале координат.

Рассматривая далее методично все случаи, придем к выводу: уравнение вида (7.9) задает одну из следующих фигур: эллипс, гиперболу, параболу, пару пересекающихся прямых, пару параллельных прямых, прямую, точку или пустое множество.

Контрольные вопросы к лекции №7

1. Понятие кривых второго порядка: эллипса, гиперболы, параболы.

2. Уравнение эллипса, каноническое уравнение эллипса.

3. Понятия фокусов эллипса; фокальных радиусов; директрисы и эксцентриситета эллипса.

4. Каноническое уравнение гиперболы.

5. Фокусы и фокальные радиусы гиперболы, асимптота гиперболы.

6. Каноническое уравнение параболы.

7. Приведение уравнения второй степени к каноническому виду.

ТЕМА 3. ЛИНЕЙНАЯ АЛГЕБРА

Лекция 8. Понятие евклидова пространства

Основные понятия:

евклидово пространство; 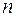–мерный вектор; неравенство Коши-Буняковского; коллинеарные векторы; неколлинеарные векторы; сонаправленные векторы; противоположно направленные векторы; линейная комбинация векторов; линейно зависимые векторы; линейно независимые векторы; размерность линейного пространства; базис векторного пространства.

N-мерные векторы

Декартово произведение множества действительных чисел 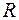само на себя состоит из всевозможных упорядоченных числовых пар. Это множество обозначают 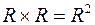и его можно отождествить с плоскостью. Множество 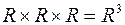состоит из упорядоченных троек и представляет собой трехмерное пространство. Если осуществить декартово произведение 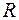на себя 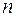раз, можно получить множество всех точек 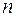-мерного пространства 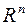. Каждый элемент пространства 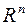представляет собой последовательность 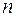чисел и записывается в виде 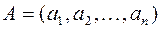. Число 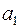называется первой координатой 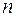-мерного вектора 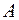, 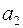– второй координатой и т.д., а число 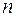– размерностью вектора 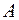. В ряде случаев в пространстве 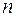–мерных векторов также бывает возможно определить операцию скалярного произведения векторов 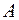и 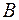через операции над их координатами.

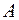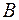В общем случае и – это 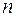–мерные векторы, т.е. 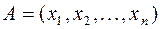, и 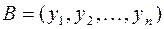. Их скалярное произведение равно сумме попарных произведений их соответствующих координат, т.е. 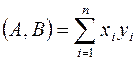. Длиной –мерного вектора 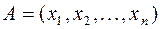называется число 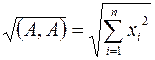. Скалярное произведение 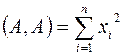называется скалярным квадратом вектора 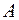и обозначается 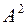. Поскольку скалярный квадрат является суммой квадратов координат вектора 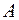, то его значение будет неотрицательным, причем 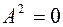тогда и только тогда, когда все координаты этого вектора равны нулю, т.е. вектор 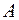– нулевой.

Пространство 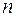–мерных векторов, в котором определена операция скалярного произведения, называется евклидовым пространством.

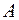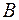Теорема. Если и – это 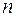–мерные векторы евклидова пространства, то справедливо неравенство:

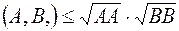
Доказательство: Рассмотрим вектор 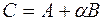, где 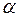– любое действительное число. Поскольку 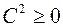, то на основании свойств скалярного произведения можно записать:

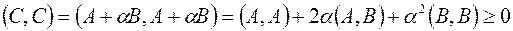
Если предположить, что 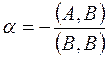, то справедливо следующее:

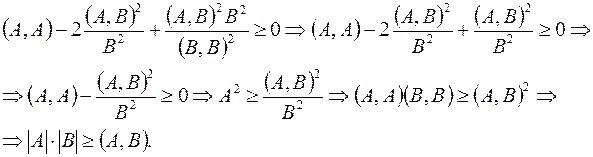
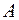Доказанное неравенство называется неравенством Коши-Буняковского. Причем, равенство имеет место тогда и только тогда, когда векторы и линейно зависимы. В общем случае, угол между векторами и 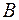можно определить как решение уравнения:

.

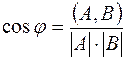Таким образом, в евклидовом пространстве 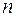–мерных векторов скалярное произведение любых двух векторов 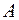и 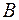равно:

.

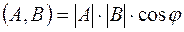Теорема. Ненулевые 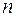–мерные векторы 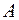и 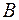равны тогда и только тогда, когда угол между этими векторами равен нулю и длины их равны.

Доказательство:

Необходимость:

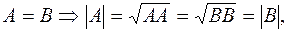
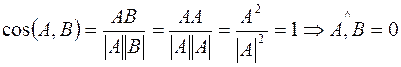
Достаточность:

Пусть 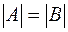и

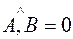
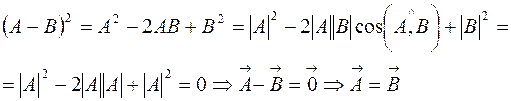
Коллинеарные векторы

Два ненулевых 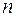-мерных вектора 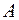и 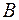называются коллинеарными, если угол между ними равен 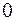или .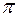

Если 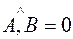, то коллинеарные векторы называются сонаправленными или одинаково направленными .

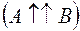Если 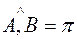, то коллинеарные векторы называются противоположно направленными .

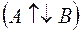Если условие коллинеарности между векторам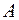и и 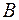не выполняется (т.е. 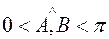), то такие вектора называются неколлинеарными.

Теорема. Ненулевые векторы 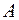и 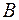коллинеарны тогда и только тогда, когда найдется такое ненулевое числ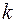о , что .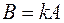

Доказательство:

Необходимость:

1. .

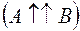
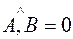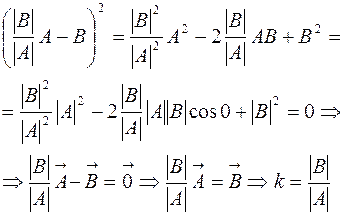
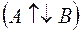
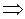
2. 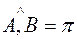. Для этого случая аналогично доказывается, что 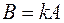, при .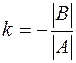

Достаточность:

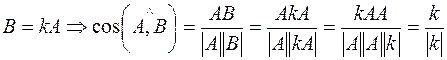
Число 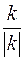имеет только два значения: 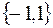. Это означает, что 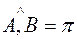или 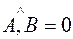, соответственно. Таким образом, вектора 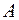и 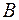коллинеарны.