Комбинаторика. Размещения. Перестановки. Сочетания

Комбинаторика. Размещения. Перестановки. Сочетания

Соединения - различные подмножества множества X={x₁, x₂,..., x_n}, содержащие m элементов, причем 1 £ m £ n.

Размещения из m элементов по n - это соединения, содержащие каждое по m элементов из n элементов множества Х, которые отличаются либо самими элементами, либо их порядком.

Число всевозможных размещений из n элементов по m в каждом равно:

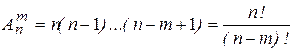, где n! = 1'2'3 ... (n-1) ' n.

Например, имеется 6 учебных дисциплин, в расписании стоит 4 пары занятий в день. Число вариантов расписания на день 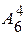=6*5*4*3=360.

Перестановки - это соединения, каждое из которых содержит n элементов и которые отличаются друг от друга только порядком элементов, т.е. это размещения из n элементов по n.

Число перестановок из n элементов равно P_n = n!.

Сочетания из n элементов множества Х по m - это соединения, которые отличаются по крайней мере одним элементом. Т.е. подмножества из m элементов множества n элементов, порядок которых не играет роли (различия в порядке элементов не меняют подмножества).

Число сочетаний из n элементов по m (n V m) в каждом равно:

.

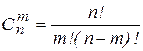Случайные события. Несовместные события.

Сумма событий. Произведение событий

Теория вероятностей занимается изучением законо­мерностей случайных событий и случайных величин при массовом их проявлении.

Под случайнымсобытием в теории вероятностей пони­мается событие, которое в результате опыта (испытания) может произойти или не произойти.

Событие называется достоверным, если оно обязательно появится в результате данного опыта, и невозможным, если оно не может появиться в этом опыте. События A₁, A₂,''', A_n называются попарно несовместными, если наступление одного из них исключает появление любого другого. СуммойA₁+A₂+'''+A_n событий A₁, A₂,'', A_n называется событие, состоящее в появлении хотя бы одного из этих событий. ПроизведениемA₁A₂'''A_n событий A₁, A₂,''', A_n называется событие, состоящее в одновременном появлении всех этих событий.

Основные теоремы теории вероятностей

Теорема сложения.

Вероятность суммы двуx несовместных событий:

P(A + В) = 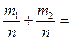P(A) + P(B)

Вероятность суммы двуx совместных событий:

P(A + В) = 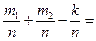P(A) + P(B) - P(AB).

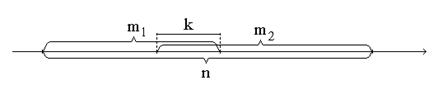
Пусть А и 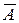- противоположные события, тогда:

P(A) + Р( 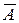) = 1.

Теорема умножения вероятностей.

Событие В называется независимым от А, если появление события А не изменяет вероятности наступления события В.

Условной вероятностью P(B/A) (или Р_А(В) )называют вероятность события В, вычисленную в предположении, что событие А уже произошло.

По определению:

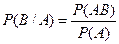
Вероятность совместного появления двух событий A и B равна:

Р(АВ) = P(A)Р(В/A).

Для независимых событий A₁, A₂,…, A_n:

P(A₁A₂...A_n) = P(A_l)P(A₂)...P(A_n).

Вероятность появления хотя бы одного из событий A₁, A₂,''', A_n, независимых в совокупности, равна:

P(A)= 1- q₁'q₂ ...q_n,

где q₁, q₂ ...q_n — вероятности появления каждого из событий A₁,A₂,'',A_n соответственно.

Формула полной вероятности.

Говорят, что события H₁, H₂, ... , H_n образуют полную группу событий, если они несовместны и при испытании обязательно наступает одно из них. Пусть H₁, H₂, ... , H_n - полная группа событий. События Н_i называют гипотезами и 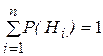. Пусть в результате испытания произошло событие A. Тогда вероятность события A находится по формуле полной вероятности:

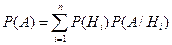
Формула Байеса.

Пусть в результате испытания событие А произошло и H₁, H₂, ... , H_n - полная группа событий. При таком условии вероятности гипотез можно подсчитать по формуле Байеса:

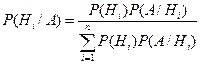
Примеры решения задач

1. Найти вероятность того, что при бросании двух игральных костей выпадет ровно 9 очков.

Решение. Общее число элементарных исходов n=36. Число благоприятных исходов m=4 (3+6, 4+5, 5+4, 6+3). Вероятность:

Р(А) = n/m = 4/36 = 1/9 » 0.111

Ответ: вероятность того, что выпадет 9 очков, равна 0.111.

2. Две зенитные установки выпускают ракеты по самолету. Вероятность попадания первой ракеты 0.8, второй – 0.9. Найти вероятность поражения цели.

Решение. Рассмотрим события: А – попадание первой ракеты, В – попадание второй ракеты. События А и В – совместные. Сумма событий:

Р(А+В) = Р(А) + Р(В) - Р(АВ) = 0.8 + 0.9 - 0.8*0.9 = 0.98

Ответ: вероятность поражения цели 0.98.

3. На склад поступило 3 партии изделий: первая - 2000 штук, вторая - 3000 штук, третья - 1000 штук. Средний процент нестандартных изделий в первой партии 10%, во второй - 5%, в третьей - 15%. Найти вероятность того, что наудачу взятое со склада изделие будет стандартным.

Решение. Всего изделий 2000+3000+1000=6000 штук. Рассмотрим гипотезы: Н₁ – изделие из первой партии, Н₂ – изделие из первой партии, Н₃ – изделие из первой партии. Их вероятности:

Р(Н₁) = 2000/6000=1/3; Р(Н₂) = 3000/6000 = 1/2; Р(Н₃) = 1000/6000 = 1/6

Событие А – наудачу взятое изделие стандартное. Условные вероятности:

Р(А/Н₁) = 0.9; Р(А/Н₂)= 0.95; Р(А/Н₃)= 0.85

Полная вероятность:

Р(А) = Р(Н₁)* Р(А/Н₁) + Р(Н₂)*Р(А/Н₂) + Р(Н₃)*Р(А/Н₃) =

=1/3*0.9 + 1/2*0.95 + 1/6*0.85 = 0.917

Ответ: вероятность того, что наудачу взятое со склада изделие будет стандартным, равна 0.917.

4. В пирамиде 15 снайперских винтовок, из них 5 СС-В и 10 СВД. Вероятность поражения цели из СС-В – 0.9, из СВД – 0.8. Снайпер поразил цель из наудачу взятой винтовки. Что вероятнее, выстрел был произведен из СС-В или из СВД?

Решение. Рассмотрим гипотезы: Н₁ – взята винтовка СС-В, Н₂ – взята винтовка СВД.

Р(Н₁)= 5/15 = 1/3; Р(Н₂)= 10/15 = 2/3

Событие А – цель поражена. Условные вероятности:

Р(А/Н₁)= 0.9; Р(А/Н₂) = 0.8

По формуле Байеса:

Р(Н₁/А)=Р(Н₁)*Р(А/Н₁)/(Р(Н₁)*Р(А/Н₁)+Р(Н₂)*Р(А/Н₂))= 0.36

Р(Н₂/А)=Р(Н₂)*Р(А/Н₂)/(Р(Н₁)*Р(А/Н₁)+Р(Н₂)*Р(А/Н₂))= 0.64

Ответ: вероятность того, что цель была поражена из винтовки СВД, выше, чем из винтовки СС-В.

Тема 6. Дискретная случайная величина (ДСВ). Функция и характеристики распределения ДСВ

Задан закон распределения ДСВ X (см. ниже варианты заданий).

Найти:

а) неизвестную вероятность р;

б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s случайной величины;

в) функцию распределения F(x) и построить её график;

г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = f(x).

Варианты заданий по теме 6:

0)

xi	-2	-1
pi	0,01	p	0,23	0,28	0,19	0,11	0,06

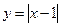
1)

xi	-2	-1
pi	0,2	0,31	0,24	p	0,07	0,04	0,01

y = 2x + 3

2)

xi	-2	-1
pi	0,04	0,08	0,3	0,3	0,1	0,08	p

y = x²– 1

3)

xi	-2	-1
pi	0,42	0,23	р	0,10	0,06	0,03	0,01

y = –2x + 1

4)

xi	-2	-1
pi	р	0,29	0,12	0,15	0,21	0,16	0,04

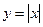
5)

xi	-2	-1
pi	0,05	0,12	0,18	0,30	р	0,12	0,05

y = 5x – 2

6)

xi	-2	-1
pi	0,16	0,25	0,25	0,16	0,10	р	0,03

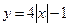
7)

xi	-2	-1
pi	0,06	р	0,12	0,2	0,3	0,1	0,03

y = x²+ 2

8)

xi	-2	-1
pi	0,02	0,38	0,30	р	0,08	0,04	0,02

y = x²+ 3

9)

xi	-2	-1
pi	0,08	0,1	0,14	0,1	0,1	0,1	р

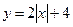
Тема 7. Непрерывная случайная величина (НСВ). Функция распределения и плотность вероятности НСВ

НСВ Х имеет нормальное распределение с математическим ожиданием M_x и средним квадратичным отклонением σ_x. Найти для заданных значений M_x, σ_x, a, b (см. ниже таблицу вариантов):

1) вероятность попадания СВ Х в интервал (a; b): P(a < X < b);

2) вероятность P(X < (a + b)/2);

3) сформулировать «правило трёх сигм»;

4) написать выражения для функции распределения F(x) и плотности вероятности f(x) и построить их графики;

5) на графиках указать полученные вероятности из пунктов 1 и 2;

6) найти квантиль x_0,7 и 20%-ю точку.

Варианты заданий по теме 7

Вариант	Mx	σx	a	b

Вопросы на зачет по теории вероятностей и математической статистике

1) Событие. Классификация событий.

2) Классическое определение вероятности.

3) Статистическое определение вероятности.

4) Геометрическое определение вероятности.

5) Элементы комбинаторики.

6) Действия над событиями. Свойства операций над событиями.

7) Теорема сложения вероятностей.

8) Условная вероятность события. Теорема умножения вероятностей.

9) Зависимость и независимость событий.

10) Вероятность суммы совместных событий.

11) Формула полной вероятности. Формула Байеса.

12) Теоретико-множественная трактовка основных понятий и аксиоматическое построение теории вероятностей.

13) Формула Бернулли.

14) Формула Пуассона.

15) Локальная формула Муавра-Лапласа.

16) Интегральная формула Муавра-Лапласа.

17) Случайные величины. Закон распределения дискретной случайной величины.

18) Математические операции над случайными величинами.

19) Математическое ожидание ДСВ и его свойства.

20) Дисперсия ДСВ и ее свойства.

21) Интегральная функция распределения СВ и её свойства.

22) Непрерывная случайная величина. Плотность вероятности и ее свойства.

23) Мода и медиана. Квантили и процентные точки.

24) Моменты случайных величин. Асимметрия и эксцесс.

25) Биномиальный закон распределения.

26) Закон распределения Пуассона.

27) Геометрическое распределение.

28) Равномерный закон распределения.

29) Показательный (экспоненциальный) закон распределения.

30) Нормальный закон распределения.

31) Свойства нормального закона распределения. Правило «трех сигм».

32) Законы распределения двумерной СВ.

33) Числовые характеристики системы двух случайных величин.

34) Ковариация и коэффициент корреляции. Линейная средняя квадратическая регрессия случайной величины Y на случайную величину X.

35) Закон больших чисел. Неравенство Чебышева. Центральная предельная теорема.

36) Генеральная совокупность и выборка. Вариационные ряды.

37) Эмпирическая функция распределения выборки. Полигон и гистограмма вариационного ряда.

38) Точечные статистические оценки. Свойства оценок: несмещенность, эффективность, состоятельность. Выборочные средняя и дисперсия.

39) Методы нахождения оценок. Метод моментов.

40) Методы нахождения оценок. Метод максимального правдоподобия.

41) Интервальные статистические оценки.

42) Проверка статистических гипотез. Схема проверки нулевой гипотезы.

43) Проверка гипотезы о нормальном распределении генеральной совокупности по критерию согласия Пирсона.

44) Регрессионный анализ.

45) Дисперсионный анализ.

Задачи

1) На станцию прибыли 10 вагонов разной продукции. Вагоны помечены номерами от одного до десяти. Найти вероятность того, что среди пяти выбранных для контрольного вскрытия вагонов окажутся вагоны с номерами 2 и 5.

2) Из 20 акционерных обществ (АО) четыре являются банкротами. Гражданин приобрел по одной акции шести АО. Какова вероятность того, что среди купленных акций две окажутся акциями банкротов?

3) На полке находится 10 книг, расставленных в произвольном порядке. Из них три книги по теории вероятностей, три - по математическому анализу и четыре - по линейной алгебре. Студент случайным образом достает одну книгу. Какова вероятность того, что он возьмет книгу по теории вероятностей или по линейной алгебре?

4) Контролер проверяет изделия на соответствие стандарту. Известно, что вероятность соответствия стандарту изделий равна 0,9. Какова вероятность того, что из двух проверенных изделий оба будут нестандартными, если события появления стандартных изделий независимы?

5) Контролер проверяет изделия на соответствие стандарту. Известно, что вероятность соответствия стандарту изделий равна 0,9. Какова вероятность того, что из двух проверенных изделий только одно стандартное.

6) В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди 6 взятых наудачу деталей 4 стандартные.

7) Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 4 или 3.

8) Из колоды карт (36 штук) наудачу вынимаются три карты. Найти вероятность того, что среди них окажется один туз или две дамы.

9) В магазине имеются 10 женских и 6 мужских шуб. Для анализа качества отобрали случайным образом три шубы. Определить вероятность того, что среди трех отобранных шуб окажутся только женские шубы.

10) В магазине имеются 10 женских и 6 мужских шуб. Для анализа качества отобрали случайным образом три шубы. Определить вероятность того, что среди трех отобранных шуб окажутся только женские или только мужские шубы.

11) На предприятие поступают заявки от нескольких торговых пунктов. Вероятности поступления заявок от пунктов А и В равны соответственно 0,5 и 0,4. Найти вероятность поступления заявок от пункта А или от пункта В, считая события поступления заявок от этих пунктов независимыми, но совместными.

12) На плоскости начерчены две концентрические окружности, радиусы которых 5 см и 10 см соответственно. Найти вероятность попадания наугад брошенной точки в кольцо.

13) В партии 100 изделий, из которых 4 - бракованные. Партия произвольно разделена на две равные части, которые отправлены двум потребителям. Какова вероятность того, что все бракованные изделия достанутся одному потребителю?

14) В партии 100 изделий, из которых 4 - бракованные. Партия произвольно разделена на две равные части, которые отправлены двум потребителям. Какова вероятность того, что все бракованные изделия достанутся обоим потребителям поровну?

15) В магазине было продано 21 из 25 холодильников трех марок, имеющихся в количествах 5, 7 и 13 штук. Полагая, что вероятность быть проданным для холодильника каждой марки одна и та же, найти вероятность того, что остались нераспроданными холодильники одной марки.

16) В магазине было продано 21 из 25 холодильников трех марок, имеющихся в количествах 5, 7 и 13 штук. Полагая, что вероятность быть проданным для холодильника каждой марки одна и та же, найти вероятность того, что остались нераспроданными холодильники трех разных марок.

17) По условиям лотереи «6 из 45» участник лотереи, угадавший 4, 5, 6 номеров из отобранных при случайном розыгрыше 6 номеров из 45, получает денежный приз. Найти вероятность того, что будут угаданы 4 цифры.

18) По условиям лотереи «6 из 45» участник лотереи, угадавший 4, 5, 6 номеров из отобранных при случайном розыгрыше 6 номеров из 45, получает денежный приз. Найти вероятность того, что будут угаданы 5 цифр.

19) По условиям лотереи «6 из 45» участник лотереи, угадавший 4, 5, 6 номеров из отобранных при случайном розыгрыше 6 номеров из 45, получает денежный приз. Найти вероятность того, что будет хотя бы один выигрыш.

20) Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй - 0,9; третий - 0,8. Найти вероятность того, что студент сдаст только 2-й экзамен.

21) Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй - 0,9; третий - 0,8. Найти вероятность того, что студент сдаст только один экзамен.

22) Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй - 0,9; третий - 0,8. Найти вероятность того, что студент сдаст три экзамена.

23) Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй - 0,9; третий - 0,8. Найти вероятность того, что студент сдаст по крайне мере два экзамена.

24) Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй - 0,9; третий - 0,8. Найти вероятность того, что студент сдаст хотя бы один экзамен.

25) Предприятие обеспечивает регулярный выпуск продукции при безотказной поставке комплектующих от двух смежников. Вероятность отказа в поставке продукции от первого из смежников равна 0,05, от второго - 0,08. Найти вероятность сбоя в работе предприятия.

26) На предприятии, изготавливающем замки, первый цех производит 25, второй 35, третий 40% всех замков. Барк составляет соответственно 5, 4 и 2%. Найти вероятность того, что случайно выбранный замок является дефектным.

27) На предприятии, изготавливающем замки, первый цех производит 25, второй 35, третий 40% всех замков. Барк составляет соответственно 5, 4 и 2%. Случайно выбранный замок является дефектным. Какова вероятность того, что он был изготовлен в первом цехе?

28) На предприятии работают две бригады рабочих: первая производит в среднем ¾ продукции с процентом брака 4%, вторая - ¼ продукции с процентом брака 6%. Найти вероятность того, что взятое наугад изделие окажется качественным.

29) На предприятии работают две бригады рабочих: первая производит в среднем ¾ продукции с процентом брака 4%, вторая - ¼ продукции с процентом брака 6%. Найти вероятность того, что взятое наугад изделие изготовлено второй бригадой при условии, что изделие оказалось бракованным.

30) В результате обследования были выделены семьи, имеющие по четыре ребенка. Считая вероятности появления мальчика и девочки в семье равными, определить вероятность появления в ней двух мальчиков.

31) Четыре покупателя приехали на оптовый склад. Вероятность того, что каждому из них потребуется холодильник марки «Стинол», равна 0,4. Найти вероятность того, что холодильник потребуется не менее чем двум покупателям.

32) Четыре покупателя приехали на оптовый склад. Вероятность того, что каждому из них потребуется холодильник марки «Стинол», равна 0,4. Найти вероятность того, что холодильник потребуется не более чем трем покупателям.

33) Четыре покупателя приехали на оптовый склад. Вероятность того, что каждому из них потребуется холодильник марки «Стинол», равна 0,4. Найти вероятность того, что холодильник потребуется всем четырем покупателям.

34) В новом микрорайоне поставлено 10000 домофонов на входных дверях домов. Вероятность выхода из строя одного домофона в течение месяца равна 0,0002. Найти вероятность того, что за месяц откажут пять замков.

35) Завод отправил в торговую сеть 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что при транспортировке будет повреждено более трех изделий.

36) Ряд распределения случайной величины Х имеет вид

X	-5
p	0,3	0,4	0,2	0,1

Вычислить P(Х ≥ 3,5).

37) Ряд распределения случайной величины Х имеет вид

X	-5
p	0,3	0,4	0,2	0,1

Вычислить P(|Х| < 2,5).

38) Ряд распределения случайной величины Х имеет вид

X
p	0,4	0,2	0,2	0,05	0,1	0,05

Найти M(Х), σ(Х), M(2Х²+ 3).

39) Даны законы распределения независимых случайных величин Х и Y

X	-4
p	0,1	0,5	0,4

Y
p	0,5	0,5

Найти M(Z), D(Z), если Z = (Х + Y)/2.

40) Случайная величина X задана функцией распределения вероятностей

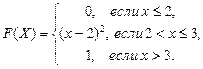
Найти плотность вероятности и вероятность попадания случайной величины Х в интервал (1; 2,5).

41) Случайная величина X задана функцией распределения вероятностей

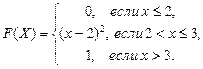
Найти математическое ожидание случайной величины Х.

42) Случайная величина X задана функцией распределения вероятностей

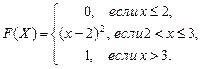
Найти среднее квадратичное отклонение случайной величины Х.

43) Плотность вероятности случайной величины X

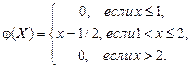
Найти функцию распределения F(X) и вероятность попадания случайной величины Х в интервал (1; 2,5).

44) Случайная величина X имеет плотность вероятности

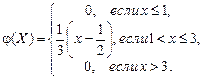
Найти медиану Me(X) и вероятность попадания случайной величины Х в интервал (1; 2,5).

45) Случайная величина X распределена равномерно на отрезке [1; 6]. Найти функцию распределения F(X), математическое ожидание, дисперсию и среднее квадратичное отклонение.

46) Случайная величина X распределена равномерно на отрезке [0; 4]. Найти функцию распределения F(X), математическое ожидание, дисперсию и среднее квадратичное отклонение.

47) Математическое ожидание и среднее квадратичное отклонение нормально распределенной случайной величины Х соответственно равны 12 и 2. Найти вероятность попадания случайной величины в интервал (14; 16), показать на графике плотности вероятности.

48) Математическое ожидание и среднее квадратичное отклонение нормально распределенной случайной величины Х соответственно равны 12 и 2. Найти вероятность попадания случайной величины в интервал (-∞; 14), показать на графике плотности вероятности.

49) Математическое ожидание и среднее квадратичное отклонение нормально распределенной случайной величины Х соответственно равны 12 и 2. Сформулировать правило «трех сигм», показать на графике плотности вероятности.

50) Математическое ожидание и среднее квадратичное отклонение нормально распределенной случайной величины Х соответственно равны 12 и 2. Найти вероятность попадания случайной величины в интервал (10; +∞), показать на графике плотности вероятности.

51) Математическое ожидание и среднее квадратичное отклонение нормально распределенной случайной величины Х соответственно равны 12 и 2. Найти квантиль уровня 0,6 и 10%-ю точку.

52) Средний расход удобрений на один гектар пашни составляет 80 кг, а среднее квадратичное отклонение расхода равно 5 кг. Считая расход удобрений нормально распределенной случайной величиной, определить диапазон, в который вносимая доза удобрений попадет с вероятностью 0,98.

53) Математическое ожидание нормально распределенной случайной величины - количества сыра, используемого для изготовления 100 бутербродов, - равно 1 кг. Известно, что с вероятностью 0,96 расход сыра на изготовление 100 бутербродов составляет от 900 до 1100 г. Определить среднее квадратичное отклонение расхода сыра на 100 бутербродов.

54) Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти вероятность того, что в течение 100 часов прибор не выйдет из строя.

55) Коробки с конфетами упаковываются автоматически. Их средняя масса равна 540 г. Известно, что 5% коробок имеют массу, меньшую 500 г. Каков процент коробок, масса которых менее 470 г?

56) Коробки с конфетами упаковываются автоматически. Их средняя масса равна 540 г. Известно, что 5% коробок имеют массу, меньшую 500 г. Каков процент коробок, масса которых менее от 500 до 550 г?

57) Коробки с конфетами упаковываются автоматически. Их средняя масса равна 540 г. Известно, что 5% коробок имеют массу, меньшую 500 г. Каков процент коробок, масса которых более 550 г?

58) Коробки с конфетами упаковываются автоматически. Их средняя масса равна 540 г. Известно, что 5% коробок имеют массу, меньшую 500 г. Каков процент коробок, масса которых отличается по абсолютной величине от средней не более, чем на 30 г?

59) Коробки с конфетами упаковываются автоматически. Их средняя масса равна 540 г. Известно, что 5% коробок имеют массу, меньшую 500 г. С помощью правила трех сигм найти границы, в которых будет находиться масса коробки.

60) Найти вероятность попадания в интервал (2; 5) случайной величины Т, имеющей показательное распределение

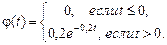
61) Найти математическое ожидание и дисперсию случайной величины X, заданной функцией распределения вероятностей

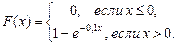
62) Имеется таблица распределения двумерной случайной величины (X, Y):

Y X
	0,07	0,16	0,1
	0,13	0,09	0,18
	0,1	0,05	0,12

Составить таблицы распределения вероятностей для каждой из величин X и Y.

63) Имеется таблица распределения двумерной случайной величины (X, Y):

Y X
	0,07	0,16	0,1
	0,13	0,09	0,18
	0,1	0,05	0,12

Найти условный закон распределения X при Y = 4.

64) Имеется таблица распределения двумерной случайной величины (X, Y):

Y X
	0,07	0,16	0,1
	0,13	0,09	0,18
	0,1	0,05	0,12

Найти условный закон распределения Y при X = 3.

65) Имеется таблица распределения двумерной случайной величины (X, Y):

Y X
	0,07	0,16	0,1
	0,13	0,09	0,18
	0,1	0,05	0,12

Найти регрессию Y на X для значения x₂ = 2.

66) Имеется таблица распределения двумерной случайной величины (X, Y):

Y X
	0,07	0,16	0,1
	0,13	0,09	0,18
	0,1	0,05	0,12

Найти регрессию X на Y для значения y₁ = 2.

67) Найти распределение относительных частот, основные характеристики вариационного ряда, построить эмпирическую функцию распределения, полигон относительных частот, найти выборочные характеристики (среднюю, дисперсию, СКО), несмещенную выборочную дисперсию, найти асимметрию и эксцесс.

xi
ni

68) Найти доверительный интервал с надежностью 0,8 для оценки математического ожидания нормально распределенной СВ X со средним квадратичным отклонением σ_x = 5, выборочной средней 20 и объемом выборки n = 25.

Комбинаторика. Размещения. Перестановки. Сочетания

Соединения - различные подмножества множества X={x₁, x₂,..., x_n}, содержащие m элементов, причем 1 £ m £ n.

Размещения из m элементов по n - это соединения, содержащие каждое по m элементов из n элементов множества Х, которые отличаются либо самими элементами, либо их порядком.

Число всевозможных размещений из n элементов по m в каждом равно:

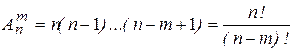, где n! = 1'2'3 ... (n-1) ' n.

Например, имеется 6 учебных дисциплин, в расписании стоит 4 пары занятий в день. Число вариантов расписания на день 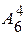=6*5*4*3=360.

Перестановки - это соединения, каждое из которых содержит n элементов и которые отличаются друг от друга только порядком элементов, т.е. это размещения из n элементов по n.

Число перестановок из n элементов равно P_n = n!.

Сочетания из n элементов множества Х по m - это соединения, которые отличаются по крайней мере одним элементом. Т.е. подмножества из m элементов множества n элементов, порядок которых не играет роли (различия в порядке элементов не меняют подмножества).

Число сочетаний из n элементов по m (n V m) в каждом равно:

.
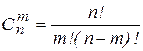