РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 4

РАСЧЕТ ПЛОСКОЙ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ

РАМЫ МЕТОДОМ ПЕРЕМЕЩЕНИЙ

Литература: [2, c. 3–21], [3, c. 380–419], [4, c. 187–203],

[5, c. 398–413], [6, c. 202–223].

Исходные данные к работе определяются по табл. 4.1 и схемам, представленным на рис. 4.1.

Таблица 4.1

Исходные данные к РГР № 4

Первая цифра шифра	F1, кН	F2, кН	Вторая цифра шифра	q1, кН/м	q2, кН/м	Третья цифра шифра (№ схемы)	l, м	h, м	α

Последовательность расчета

4.1. Вычертить в масштабе расчетную схему рамы с указанием размеров, величин нагрузок и соотношений жесткостей.

4.2. Определить степень кинематической неопределимости рамы (число неизвестных метода перемещений) n_к = n_у + n_л , где n_у − число жестких узлов расчетной схемы, способных к повороту при ее деформации; n_л − число возможных линейных смещений всех узлов расчетной схемы.

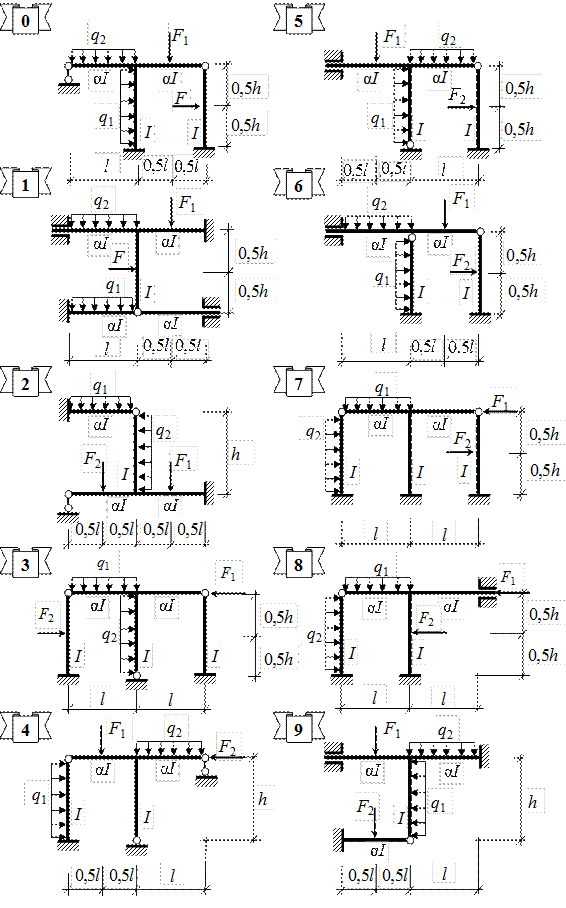
Рис. 4.1. Схемы заданий к РГР № 4

4.3. Получить основную систему метода перемещений, введя дополнительные связи по направлениям возможных углов поворота жестких узлов и линейных смещений всех узлов

Расчет в классической форме

4.4. Записать систему канонических уравнений метода перемещений в общем виде применительно к заданной схеме рамы.

4.5. Построить в основной системе метода перемещений деформированные схемы от последовательных единичных смещений по направлению дополнительных связей.

4.6. Используя таблицы реакций (пп. 1–4 прил. 1), построить в основной системе эпюры 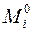от указанных в п.4.5 единичных смещений.

4.7. Используя таблицы реакций (пп. 5–8 прил. 1), построить в основной системе эпюру 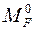от заданного загружения.

4.8. Определить коэффициенты при неизвестных (реакции в дополнительных связях от единичных смещений) и свободные члены (реакции в дополнительных связях от действия внешней нагрузки) системы канонических уравнений.

Указания:

· Реакции в дополнительных угловых связях определяются непосредственно из равновесия жесткого узла, в который введена угловая связь.

· Реакции в дополнительных линейных связях ортогональных рам определяются из условия равновесия отсеченной части основной системы. При этом сечения (сквозные или замкнутые) проводятся параллельно оси линейной связи через все стержни схемы, получившие деформации (см. п. 4.4) при смещении данной связи.

· Реакция в дополнительной связи считается положительной, если она направлена в сторону заданного в п. 4.4. смещения этой связи.

· Все схемы по определению реакций в дополнительных связях должны быть приведены на чертеже.

4.9. Записать систему канонических уравнений метода перемещений в численном виде и из ее решения найти неизвестные Z_i.

4.10. Определить изгибающие моменты в основной системе от действительных смещений по направлению дополнительных связей (построить эпюры) и на основании принципа независимости действия сил построить эпюру изгибающих моментов в заданной расчетной схеме

.

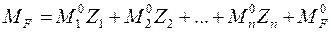4.11. Произвести проверки правильности построения эпюры :

·Для каждого жесткого узла заданной расчетной схемы должно выполняться уравнение равновесия.

· Для всей рамы должна выполняться деформационная проверка расчета. Для этого выбирается любая наиболее простая статически определимая основная система, получаемая из заданной путем удаления лишних связей. В выбранной статически определимой основной системе строится суммарная эпюра изгибающих моментов 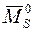от единичных сил, приложенных по направлению удаленных связей. Проверка считается выполненной, если

.

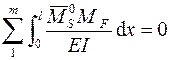4.12. Построить эпюру поперечных сил в заданной расчетной схеме на основании дифференциальной зависимости Q_F = dM/dx.

4.13. Определить продольные силы во всех стержнях расчетной схемы из условия равновесия ее узлов и построить эпюру N_F.

4.14. Произвести статическую проверку расчета: любая отсеченная часть расчетной схемы или вся схема, отсеченная от опор, под действием внутренних и внешних сил должна находиться в равновесии, т.е. должны выполняться три уравнения равновесия 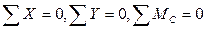(c– любая точка на плоскости).

Для выполнения этой проверки рекомендуется рассмотреть два случая:

· Равновесие всей расчетной схемы, отсеченной от опор.

· Равновесие любой отсеченной части расчетной схемы

Расчет в матричной форме[1]

4.15. Вычертить основную систему метода перемещений (п. 4.2) и на ней показать порядок обхода стержней расчетной схемы и пронумеровать расчетные сечения в соответствии с намеченным обходом.

4.16. Составить матрицы жесткости отдельных стержней рамы:

· для участков c одним расчетным сечением

;

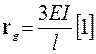· для участков с двумя расчетными сечениями

.

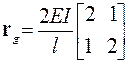4.17. Составить квазидиагональную матрицу жесткости не объединенных элементов 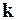(m x m), где m – число расчетных сечений рамы. В общем виде эта матрица имеет вид

.

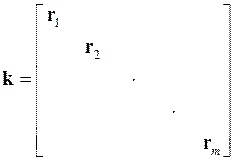4.18. По деформированным схемам, построенным в основной системе от единичных смещений по направлению дополнительных связей (п. 4.4), определить углы поворота расчетных сечений и составить матрицу преобразования деформаций 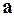порядка (m x n), где n – число неизвестных метода перемещений.

4.19. По эпюре (см. п. 4.6) составить матрицу усилий в основной системе метода перемещений 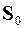(m´p), где p – число вариантов загружения (для данной РГР p = 1).

4.20. Составить матрицу 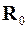свободных членов системы канонических уравнений (n x p), используя результаты расчета в классической форме (см. п. 4.7).

4.21. Выполнить ниже перечисленные матричные операции.

· Транспонировать матрицу .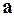

· Получить матрицу усилий в расчетных сечениях основной системы от единичных смещений по направлению дополнительных связей

.

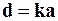· Получить матрицу коэффициентов при неизвестных

.

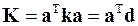· Выполнить обращение матрицы 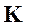и произвести проверку обращения

,

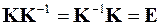где 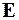– единичная матрица.

· Определить неизвестные метода перемещений

.

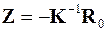· Определить усилия в основной системе метода перемещений от действительных смещений по направлению дополнительных связей

.

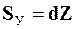· Получить матрицу усилий в заданной расчетной схеме

.

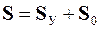· Сравнить значения элементов матрицы 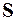, с усилиями, полученными классической формой расчета (п. 4.10).

4.22. Произвести проверку правильности произведенного расчета. Для этого по эпюре 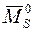(см. п. 4.11) составить матрицу усилий .

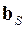Деформационная проверка расчета в матричном виде будет иметь вид:

,

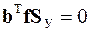где 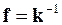─ матрица податливости необъединенных элементов расчетной схемы.

РАСЧЕТНО-ГРАФИЧЕСКАЯ № 5

ДИНАМИЧЕСКИЙ РАСЧЕТ ПЛОСКОЙ РАМЫ

С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ НА ДЕЙСТВИЕ ВИБРАЦИОННОЙ НАГРУЗКИ

Литература: [2, c. 178–197], [8, c. 124–220], [9, c. 3–61],

[11, c. 54–65, 69–82].

Исходные данные к работе определяются по табл. 5.1 и схемам, представленным на рис. 5.1.

Таблица 5.1

Исходные данные к РГР № 5

Первая цифра шифра	m, т	β	Вторая цифра шифра		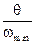α	F1, кН	F2, кН	Третья цифра шифра (№ схемы)	l, м	h, м	EI1, кН·м2
	0,5			0,5	1,5
	0,6	1,5		0,55
	0,7			0,6	2,5
	0,8	2,5		0,65
	0,9			0,7	1,5
	1,0			0,68
	1,1	1,5		0,8	2,5
	1,2			0,72
	1,3	2,5		0,66	3,5
	1,4			0,58

Примечание. В таблице приведены амплитудные значения вибрационной нагрузки F_i (t) = F_i sin θt.

Последовательность расчета

5.1. Вычертить в масштабе заданную расчетную схему рамы с указанием размеров, величин масс, вибрационной нагрузки и соотношения жесткостей стержней.

5.2. Определить число степеней свободы сосредоточенных масс заданной расчетной схемы.

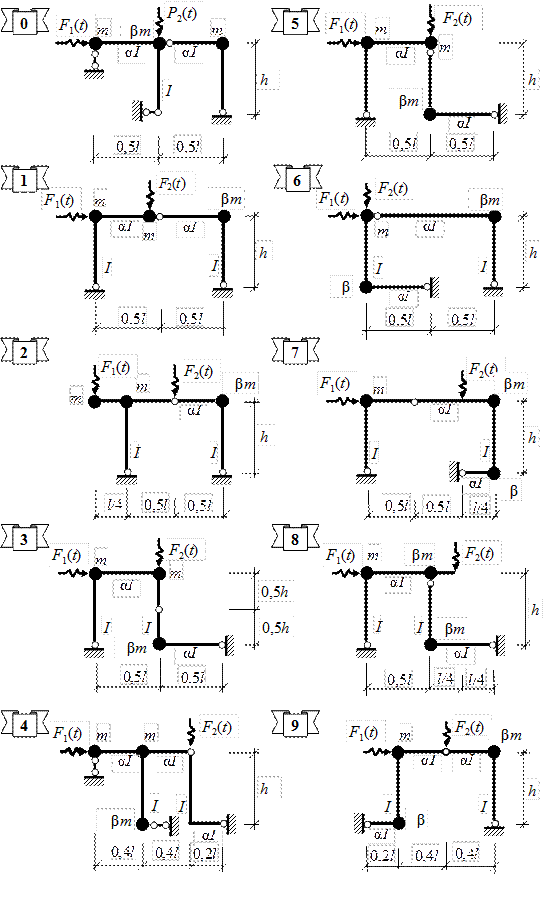
Рис. 5.1. Схемы заданий к РГР № 5

5.3. Показать расчетную схему рамы при действии амплитудных значений инерционных сил и вибрационной нагрузки.

5.4. Записать в общем виде уравнение частот свободных колебаний применительно к заданной расчетной схеме.

5.5. По направлению возможных смещений масс последовательно приложить единичные силы и от действия каждой из них построить эпюры изгибающих моментов M_i.

5.6. Определить коэффициенты уравнения частот

,

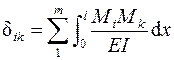где m – число участков интегрирования.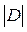

5.7. Составить уравнение частот в численном виде.

5.8. Определить корни частотного уравнения l_i (i = 1 … n) и произвести проверки правильности его решения:

,

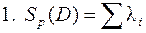где S_p (D) – след (сумма главных коэффициентов) матрицы, составленной из коэффициентов частотного уравнения; 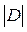– величина определителя этой матрицы

5.9. Определить частоты и периоды свободных колебаний масс.

5.10. Вычислить относительные амплитуды масс и построить формы колебаний для каждой частоты.

5.11. Из определенного в п. 5.7 спектра частот свободных колебаний выявить наименьшее значение ω_min и определить круговую частоту вынужденных колебаний по заданному в табл. 5.1 соотношению.

5.12. Показать расчетную схему рамы при действии на нее амплитудных значений нагрузок и инерционных сил.

5.13. Записать в общем виде систему канонических уравнений для определения амплитудных значений инерционных сил применительно к заданной расчетной схеме.

5.14. Построить в заданной расчетной схеме эпюру изгибающих моментов M_F от действия амплитудных значений вибрационной нагрузки.

5.15. Определить главные коэффициенты системы канонических уравнений

.

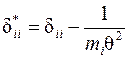Побочные коэффициенты системы канонических уравнений имеют те же значения, что и в уравнении частот.

5.16. Определить свободные члены системы канонических уравнений

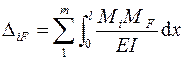
5.17. Записать систему канонических уравнений в численном виде и из ее решения определить амплитудные значения инерционных сил J_i.

5.18. Построить динамическую эпюру изгибающих моментов

M_дин = M₁ J₁ + M₂ J₂ + …+M_n J_n + M_F.

5.19. Определить амплитуды масс a_i = J_i/m_i∙θ² и построить деформированную схему рамы при вынужденных колебаниях.