Норма вектора в евклидовом пространстве
1. Норма вектора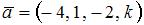 
, 
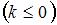в евклидовом пространстве со стандартным скалярным произведением равна 5 при 
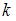равном …(-2).
2 Если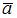 
и 
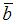– ортогональные векторы из евклидова пространства со стандартным скалярным произведением, такие что 
, 
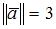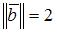, то норма вектора 
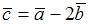равна …(5)
3.Есл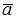и 
и 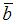– ортогональные векторы из евклидова пространства со стандартным скалярным произведением, такие что 
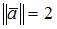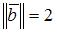, , то норма вектора 
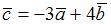равна …(10)
4. Даны векторы 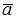и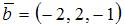 
, угол между которыми равен 
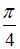. Тогда проекция вектора 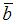на вектор 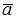равна … 
.
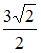5. Скалярное произведение векторов 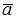и 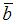равно 5, угол между векторами равен 
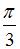, норма вектора 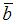равна 2. Тогда норма вектора 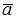равна …(5)
6. Скалярное произведение векторов 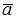и 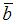равно 8, угол между векторами равен 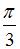, норма вектора 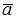равна 4. Тогда норма вектора 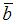равна …(4)
7. Даны векторы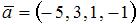 
и 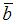, угол между которыми равен 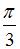. Тогда проекция вектора 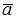на вектор 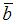равна …(3)
Векторное произведение векторов.
1*. Даны два вектора: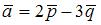 
и 
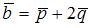, где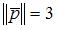 
, 
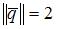, угол между векторами 
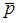и 
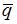равен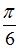 
. Тогда модуль векторного произведения векторов 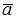и 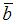будет равен …(21)
2.Даны два вектора: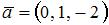 
и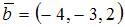 
. Тогда вектор 
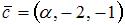будет перпендикулярен и вектору 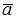, и вектору 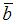, при 
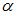равном …(1)
3. Даны два вектора: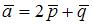 
и 
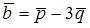, где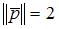 
, 
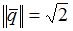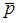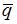, угол между векторами и равен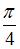 
. Тогда площадь параллелограмма, построенного на векторах 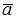и 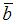, будет равна …(14)
4. Площадь параллелограмма, построенного на векторах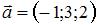 
и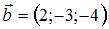 
, равна …( 
)
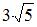5. Даны два вектора: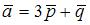 
и 
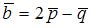, где ,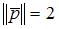 
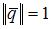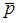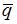, угол между векторами и равен 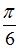. Тогда площадь треугольника, построенного на векторах 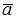и 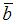будет равна …(2,5).
6. Даны два вектора: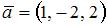 
и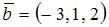 
. Тогда вектор 
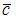, перпендикулярный и вектору 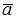и вектору 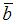, можно представить в виде …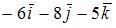 
7. Площадь треугольника, образованного векторам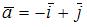и 
и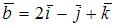 
, равна …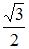 
8. Площадь треугольника с вершинами в точках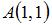 
, 
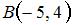и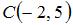 
равна …(7,5)
3. Градиент.
1. Градиент скалярного поля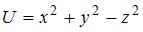 
в точке 
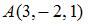равен …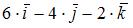 
2. Модуль градиента скалярного поля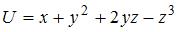 
в точке 
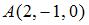равен …(3).
3. Градиент скалярного поля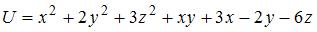 
равен нулевому вектору в точке …(-2, 1, 1)
4. Модуль градиента скалярного поля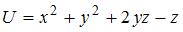 
в точке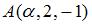 
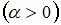равен 7 при 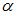равном …(3).
5. Модуль градиента скалярного поля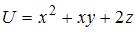 
в точке 
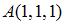равен …( 
).
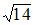6. Модуль градиента скалярного поля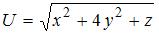 
в точке пересечения оси 
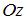с поверхностью 
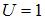равен …(1/2)
7. Градиент скалярного поля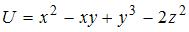 
в точке 
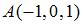равен ….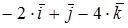 
ДЕ 5. Функциональный анализ
ПРИМЕРЫ
- Мера плоского множества
1.Мера плоского множества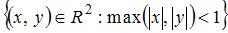 
равна …(4)
2. Мера плоского множества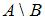 
, где А= 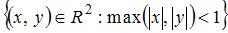и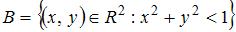 
равна …( 
)
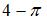3. Плоская мера отрезка [0; 1], лежащего на оси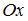 
в плоскости 
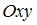равна …(0)
4. Мера плоского множества, изображенного на рисунке, равна …(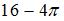 
)
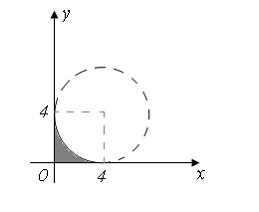
5. Мера плоского множества, изображенного на рисунке,
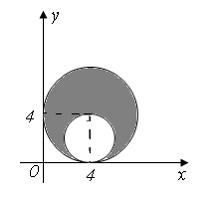равна …( 
)
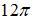6. Мера плоского множества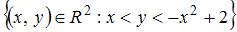 
равна …(4,5)
7. Плоская мера множества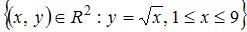 
равна …(0)
8. Мера плоского множества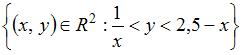 
равна …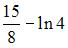 
Элементы теории множеств
1. Даны три множества: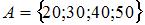 
, 
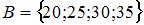и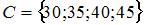 
. Тогда число элементов множества 
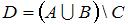равно …(3)
2. Даны три множества: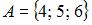 
, 
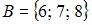и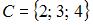 
. Тогда число элементов множества 
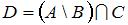равно …(1)
3. Даны множества: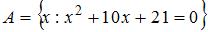 
, 
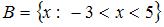. Тогда число целых чисел, принадлежащих их объединению равно …(9)
4. Даны три множества: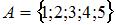 
, 
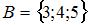и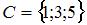 
. Тогда число элементов множества 
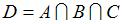равно …(2)
5. Даны три множества: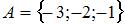 
, 
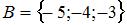и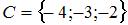 
. Тогда число элементов множества 
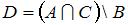равно …(1)
6. Даны два множества: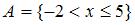 
и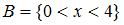 
. Тогда количество целых значений 
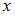, принадлежащих разности множеств 
\ 
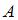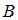, равно …(4)
7. Даны множества: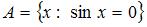 
и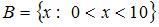 
. Тогда число элементов, принадлежащих их пересечению равно (3: π, 2π, 3π)
8. Даны три множества: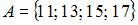 
, 
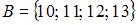и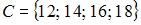 
. Тогда число элементов множества 
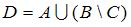равно …(5)
Отображения множеств
1. Прообразом множества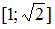 
при отображении 
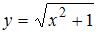является …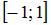 
2. Прообразом множества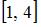 
при отображении 
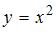является …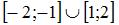 
3.Биективное (взаимно однозначное!)отображение отрезка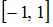 
на отрезок 
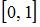может быть задано функцией …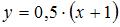 
4. Отображение, действующее из отрезка 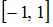на действительную числовую ось и имеющее обратное отображение, может быть задано функцией …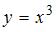 
5. Отображение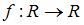 
действует по правилу: 
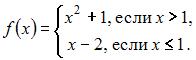Тогда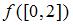 
имеет вид …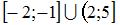 
6. Обратимым на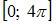 
является отображение …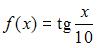 
7. Образом отрезка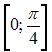 
при отображении 
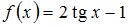является отрезок …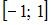 
8. Пусть задано отображение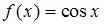 
. Тогда 
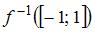имеет вид …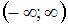 
ДЕ 6. Комплексный анализ.
ПРИМЕРЫ