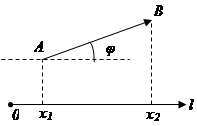Декартова система координат на плоскости и в пространстве
Лекция №4
Глава 2. ВЕКТОРНАЯ АЛГЕБРА
Декартова система координат на плоскости и в пространстве
 | Ось — прямая линия с указанным на ней направлением. |
 | Ось координат — ось, на которой заданы начало отсчёта (начало координат), единичный отрезок, и каждому действительному числу соответствует определённая единственная точка. |
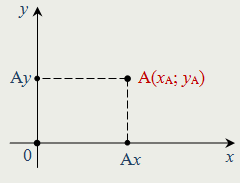 | На плоскости Декартова (прямоугольная) система координат — две взаимно перпендикулярные оси координат (ось абсцисс Ox и ось ординат Oy) с общим началом отсчёта. Каждой точке А координатной плоскости ставится в соответствие пара чисел (xA; yA) — координаты проекций точки на соответствующие оси координат. Ax(xA; 0) — проекция точки А на координатную ось Ox; Ay (0; yA)— проекция точки А на координатную ось Oу. |
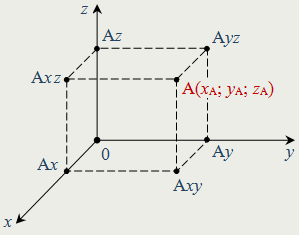 | В пространстве Декартова (прямоугольная) система координат — три взаимно перпендикулярные оси координат (ось абсцисс Ox, ось ординат Oy и ось аппликат Oz) с общим началом отсчёта. Каждой точке А координатного пространства ставится в соответствие тройка чисел (xA; yA; zA) —координаты проекций точки на соответствующие оси координат. Ax (xA; 0; 0) — проекция точки А на координатную ось Ox; Ay (0; yA; 0) — проекция точки А на координатную ось Oу; Az (0; 0; zA) — проекция точки А на координатную ось Oz; Axy (xA; yA; 0) — проекция точки А на плоскость Oxy; Axz (xA; 0; zA) — проекция точки А на плоскость Oxz; Ayz ( 0; yA; zA) — проекция точки А на плоскость Oyz. |
§2. Векторы, основные определения
def. Вектором называется направленный отрезок (отрезок, у которого различают начало и конец).
Если А – начало, В – конец, то вектор обозначают 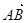 (или
(или 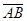 ).
).
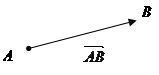 | |||
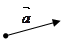 | |||
Часто вектор обозначают одной буквой 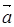 .
.
def. Длиной или модулем вектора 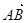 называется длина отрезка
называется длина отрезка 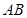 . Обозначают
. Обозначают 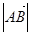 .
.
def.Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 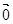 .
. 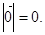
Замечание. Начало и конец нулевого вектора совпадают. Нулевой вектор направления не имеет.
Будем рассматривать только свободные векторы, т.е. те, которые можно переносить в любое место пространства, сохраняя длину и направление.
def. Векторы  и
и  , расположенные на одной прямой или параллельных прямых, называются коллинеарными. При этом пишут
, расположенные на одной прямой или параллельных прямых, называются коллинеарными. При этом пишут  çç
çç  .
.
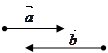 | |||
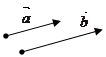 | |||
Замечание. Нулевой вектор считается коллинеарным любому вектору.
def. Векторы  и
и  называются равными, если они:
называются равными, если они:
1) имеют равные модули;
2) коллинеарны;
3) направлены в одну сторону.
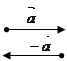 def. Вектор
def. Вектор  называется противоположным ненулевому вектору
называется противоположным ненулевому вектору  , если этот вектор имеет модуль, равный модулю вектора
, если этот вектор имеет модуль, равный модулю вектора  , коллинеарен с ним, но направлен в противоположную сторону.
, коллинеарен с ним, но направлен в противоположную сторону.
def.Векторы называются компланарными, если они лежат в одной плоскости или параллельны одной плоскости.
 |
Линейные операции над векторами. Линейное пространство
I. Сложение векторов
Правило треугольника
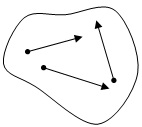
def.Суммой векторов  и
и  называется вектор
называется вектор  =
=  +
+  , который соединяет начало 1-го вектора с концом 2-го, при условии, что точка приложения 2-го вектора находится в конце 1-го. Распространяется на любое конечное число векторов.
, который соединяет начало 1-го вектора с концом 2-го, при условии, что точка приложения 2-го вектора находится в конце 1-го. Распространяется на любое конечное число векторов.
 |
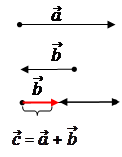
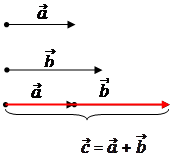 Частный случай. Сложение коллинеарных векторов.
Частный случай. Сложение коллинеарных векторов.
|
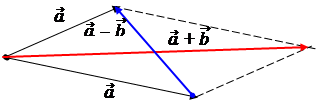
Правило параллелограмма
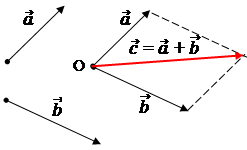
Отложить от т. О векторы  и
и  . Построить на этих векторах как на сторонах параллелограмм. Вектор, служащий диагональю параллелограмма, проведенный из т. О, является суммой
. Построить на этих векторах как на сторонах параллелограмм. Вектор, служащий диагональю параллелограмма, проведенный из т. О, является суммой  +
+  .
.
II. Вычитание векторов
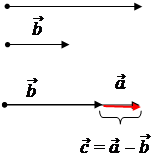
def. Разностью двух векторов  и
и  называется вектор
называется вектор  =
=  -
-  , который при сложенным с вектором
, который при сложенным с вектором  дает вектор
дает вектор  .
.
Если  =
=  -
-  , то
, то  +
+  =
=  .
.
Из определения вытекает правило построения  -
-  .
.
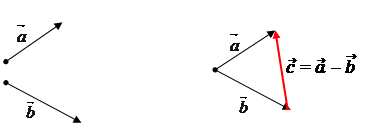 |
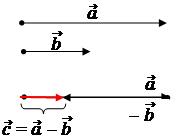
Вектор  =
=  -
-  направлен из конца вычитаемого к концу уменьшаемого.
направлен из конца вычитаемого к концу уменьшаемого.
|
 |
 Итак:
Итак:
Проекция вектора на ось
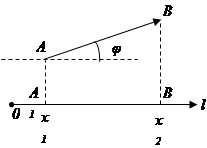 Пусть даны: l – некоторая ось и
Пусть даны: l – некоторая ось и 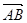 – произвольный вектор.
– произвольный вектор.
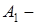 проекция А на ось l,
проекция А на ось l, 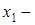 координата
координата 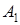 на l;
на l;
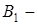 проекция B на ось l,
проекция B на ось l, 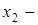 координата
координата 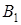 на l.
на l.
def. Проекцией вектора 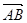 на ось называется разность
на ось называется разность 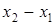
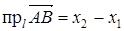 .
.
Обозначим 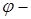 угол между
угол между 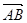 и l;
и l; 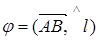 – наименьший угол, на который надо повернуть единичный вектор
– наименьший угол, на который надо повернуть единичный вектор 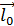 оси l до совпадения с
оси l до совпадения с 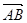 .
.
| 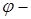 острый угол острый угол 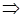 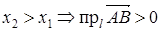 | |||
 |  тупой угол тупой угол 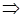 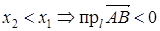 | |||
 |  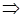 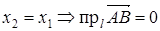 |
Свойства проекций
1. Проекция вектора 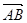 на ось l равна модулю вектора
на ось l равна модулю вектора 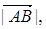 умноженному на косинус угла
умноженному на косинус угла 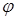 между
между 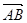 и осью l.
и осью l.
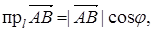 где
где 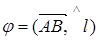 .
.
Доказательство.
1 случай. 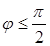
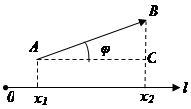
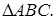
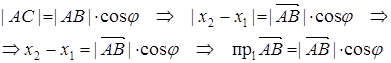
2 случай. 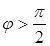
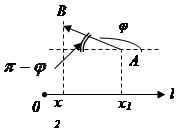
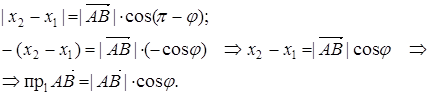
Свойство доказано.
2. Проекция суммы векторов на ось равна сумме проекций слагаемых векторов на
ту же ось.
 Доказательство.
Доказательство.
3. При умножении вектора на число проекция на ось также умножается на это число.
l ×  Þ прl (l
Þ прl (l  ) = l прl
) = l прl  .
.
Доказательство.
1 случай.  . прl (l
. прl (l  ) =
) = 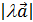 cos j = l
cos j = l 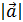 cos j = l прl
cos j = l прl  .
.
2 случай. 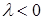 . прl (l
. прl (l  ) =
) = 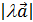 cos (p - j ) = - l
cos (p - j ) = - l 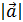 (- cos j) = l прl
(- cos j) = l прl  .
.
4. Проекции двух равных векторов на одну и ту же ось равны.
 =
=  Þ прl
Þ прl  = прl
= прl  .
.
Замечания.
1) Любые два коллинеарных вектора на плоскости линейно зависимы.
2) Любые два неколлинеарных вектора на плоскости линейно независимы.
Таким образом, для того, чтобы два вектора на плоскости были линейно независимы, необходимо и достаточно, чтобы они были неколлинеарные.
Теорема. Если на плоскости заданы два неколлинеарных вектора  и
и  , то любой третий вектор
, то любой третий вектор  плоскости может быть представлен в виде линейной комбинации векторов
плоскости может быть представлен в виде линейной комбинации векторов  и
и  , т.е.
, т.е.
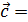 l1
l1 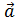 + l2
+ l2  . (1)
. (1)
Доказательство.
По условию векторы  и
и  – неколлинеарные.
– неколлинеарные.
1) Предположим, что 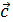 неколлинеарен векторам
неколлинеарен векторам  и
и  . Построим параллелограмм, где
. Построим параллелограмм, где  является диагональю, а стороны лежат на векторах
является диагональю, а стороны лежат на векторах  и
и  .
.
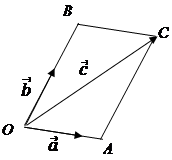
2) Пусть  коллинеарен
коллинеарен  или
или  , например,
, например,  коллинеарен
коллинеарен  Þ
Þ
Теорема доказана.
Следствие 1. Всякие три вектора на плоскости линейно зависимы.
Следствие 2. Если число данных векторов на плоскости больше трех, то они линейно зависимы.
 l1
l1 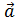 + l2
+ l2  Þ
Þ 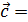 l1
l1 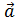 + l2
+ l2  + 0 ×
+ 0 × 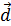 + … + 0 ×
+ … + 0 × 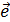 Þ линейно зависимые.
Þ линейно зависимые.
Вывод. Максимальное число линейно независимых векторов на плоскости равно двум.
Аналогично доказывается:
1. Для того чтобы три вектора в пространстве были линейно независимы, необходимо и достаточно, чтобы они были некомпланарные.
2. Если  ,
,  ,
,  - три некомпланарных вектора пространства, то любой четвертый вектор
- три некомпланарных вектора пространства, то любой четвертый вектор 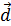 пространства может быть представлен в виде линейно комбинации векторов
пространства может быть представлен в виде линейно комбинации векторов  ,
,  ,
,  .
.
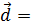 l1
l1 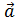 + l2
+ l2  + l3
+ l3  . (2)
. (2)
3. Всякие четыре и более векторов пространства линейно зависимы.
Вывод. Максимальное число линейно независимых векторов в пространстве равно трем.
def. Базисом на плоскости называется два любых линейно независимых вектора
плоскости, т.е. пара неколлинеарных векторов.
Базисом в пространстве называется три любых линейно независимых вектора пространства, т.е. тройка некомпланарных векторов.
Рассмотрим разложение (1) на плоскости 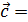 l1
l1 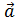 + l2
+ l2  , где
, где  и
и  - неколлинеарные.
- неколлинеарные.
Коэффициенты 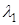 и
и 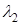 называются координатами вектора
называются координатами вектора  в базисе
в базисе  ,
,  .
.
Аналогично для разложения (2): 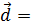 l1
l1 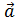 + l2
+ l2  + l3
+ l3  , где
, где  ,
,  ,
, 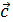 - некомпланарные векторы пространства.
- некомпланарные векторы пространства.
Коэффициенты 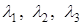 называются координатами вектора
называются координатами вектора 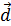 в базисе
в базисе  ,
,  ,
, 
Замечания.
1.Если определитель, составленный из координат двух векторов плоскости, отличен от нуля, то эти векторы линейно независимы на плоскости, т.е. образуют базис на плоскости.
2.Если определитель, составленный из координат трех векторов пространства R3, отличен от нуля, то эти векторы линейно независимы в пространстве, т.е. образуют базис в R3.
Пример 4.1. Доказать, что векторы  1 = (2; 0; 0),
1 = (2; 0; 0),  2 = (0; 1; 0),
2 = (0; 1; 0), 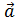 3 = (0; 0; 0,5) образуют базис в R3. Найти координаты
3 = (0; 0; 0,5) образуют базис в R3. Найти координаты 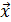 = (2; - 4; 15) в этом базисе, т.е. разложить вектор
= (2; - 4; 15) в этом базисе, т.е. разложить вектор 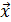 по базису
по базису  1,
1,  2,
2,  3. Ответ:
3. Ответ: 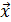 =
=  1 - 4
1 - 4  2 + 3
2 + 3  3.
3.
III. Модуль вектора
По теореме о длине диагонали параллелепипеда
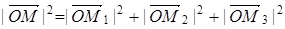 или
или 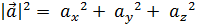 .
.
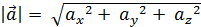 - модуль вектора
- модуль вектора  .
.
V. Направляющие косинусы
Направление вектора в пространстве определяется углами 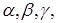 которые вектор составляет с осями Ox, Oy, Oz. Косинусы этих углов, т.е.
которые вектор составляет с осями Ox, Oy, Oz. Косинусы этих углов, т.е. 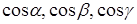 называются направляющими косинусами вектора.
называются направляющими косинусами вектора.
По свойству 1 проекций:
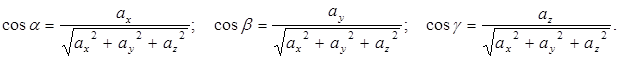
Тогда 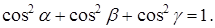
Лекция №4
Глава 2. ВЕКТОРНАЯ АЛГЕБРА
Декартова система координат на плоскости и в пространстве
 | Ось — прямая линия с указанным на ней направлением. |
 | Ось координат — ось, на которой заданы начало отсчёта (начало координат), единичный отрезок, и каждому действительному числу соответствует определённая единственная точка. |
 | На плоскости Декартова (прямоугольная) система координат — две взаимно перпендикулярные оси координат (ось абсцисс Ox и ось ординат Oy) с общим началом отсчёта. Каждой точке А координатной плоскости ставится в соответствие пара чисел (xA; yA) — координаты проекций точки на соответствующие оси координат. Ax(xA; 0) — проекция точки А на координатную ось Ox; Ay (0; yA)— проекция точки А на координатную ось Oу. |
 | В пространстве Декартова (прямоугольная) система координат — три взаимно перпендикулярные оси координат (ось абсцисс Ox, ось ординат Oy и ось аппликат Oz) с общим началом отсчёта. Каждой точке А координатного пространства ставится в соответствие тройка чисел (xA; yA; zA) —координаты проекций точки на соответствующие оси координат. Ax (xA; 0; 0) — проекция точки А на координатную ось Ox; Ay (0; yA; 0) — проекция точки А на координатную ось Oу; Az (0; 0; zA) — проекция точки А на координатную ось Oz; Axy (xA; yA; 0) — проекция точки А на плоскость Oxy; Axz (xA; 0; zA) — проекция точки А на плоскость Oxz; Ayz ( 0; yA; zA) — проекция точки А на плоскость Oyz. |
§2. Векторы, основные определения
def. Вектором называется направленный отрезок (отрезок, у которого различают начало и конец).
Если А – начало, В – конец, то вектор обозначают 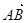 (или
(или 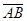 ).
).
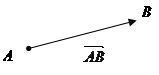 | |||
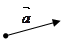 | |||
Часто вектор обозначают одной буквой 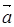 .
.
def. Длиной или модулем вектора 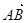 называется длина отрезка
называется длина отрезка 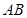 . Обозначают
. Обозначают 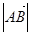 .
.
def.Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 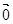 .
. 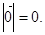
Замечание. Начало и конец нулевого вектора совпадают. Нулевой вектор направления не имеет.
Будем рассматривать только свободные векторы, т.е. те, которые можно переносить в любое место пространства, сохраняя длину и направление.
def. Векторы  и
и  , расположенные на одной прямой или параллельных прямых, называются коллинеарными. При этом пишут
, расположенные на одной прямой или параллельных прямых, называются коллинеарными. При этом пишут  çç
çç  .
.
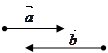 | |||
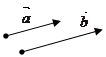 | |||
Замечание. Нулевой вектор считается коллинеарным любому вектору.
def. Векторы  и
и  называются равными, если они:
называются равными, если они:
1) имеют равные модули;
2) коллинеарны;
3) направлены в одну сторону.
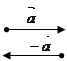 def. Вектор
def. Вектор 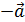 называется противоположным ненулевому вектору
называется противоположным ненулевому вектору  , если этот вектор имеет модуль, равный модулю вектора
, если этот вектор имеет модуль, равный модулю вектора  , коллинеарен с ним, но направлен в противоположную сторону.
, коллинеарен с ним, но направлен в противоположную сторону.
def.Векторы называются компланарными, если они лежат в одной плоскости или параллельны одной плоскости.
 |