Необходимый признак сходимости ряда

Теорема. Если ряд сходится, то его общий член стремится к нулю при :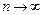

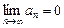. (6)

Для доказательства выразим общий член ряда (1) в виде

.

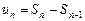Так как ряд сходится, то существует конечный предел 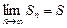. Но тогда и 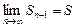. Поэтому

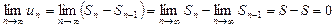
Следствие. Если предел общего члена ряда не равен нулю, то ряд расходится.

Следует заметить, что рассмотренная теорема дает лишь необходимый признак сходимости ряда, и этот признак не является достаточным. Иначе говоря, если 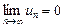, то из этого еще не следует, что ряд сходится.

Пример. Рассмотрим ряд

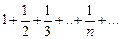, (7)

называемый гармоническим рядом. Очевидно, для него .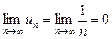

Докажем, что, несмотря на это, гармонический ряд расходится. Рассмотрим

,

.

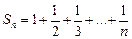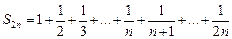Очевидно,

.

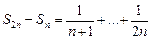Заменим в правой части слагаемые 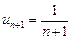, ..., 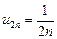на слагаемые 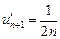, ..., 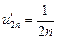. Тогда

.

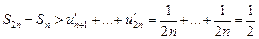Если бы ряд (6) сходился, то было бы

,

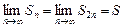следовательно, 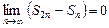. А это противоречит тому, что .

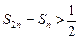Ряды с положительными членами

Теорема (признак сравнения). Пусть даны два ряда с положительными членами

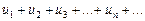(1)

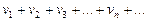(2)

и пусть для любого n выполняется неравенство

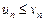. (3)

Тогда: а) если ряд (2) сходится, то сходится и ряд (1); б) если ряд (1) расходится, то расходится и ряд (2).

Доказывать эту теорему не будем.

Заметим, что при условии (3) ряд (2) называется мажорантой ряда (1), а ряд (1) соответственно минорантой ряда (2).

Примеры:

1. Исследовать сходимость ряда

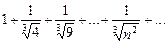
Сравним члены этого ряда с соответствующими членами гармонического ряда

.

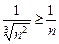Так как гармонический ряд расходится, то данный ряд также расходится.

2. Исследовать сходимость ряда

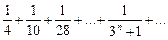
Сравним члены этого ряда с соответствующими членами геометрической прогрессии:

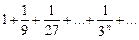
Очевидно,

,

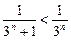и так как геометрическая прогрессия сходится, то данный ряд также сходится.

Заметим, что в рассмотренных примерах мы применяли в качестве эталонов ряды, которые часто используются для сравнения.

1) гармонический ряд

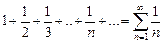
(расходится);

2) геометрическая прогрессия

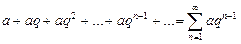
(сходится при 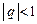, расходится при ).

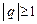Добавим к ним

3) обобщенный гармонический ряд

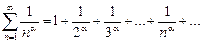
Можно доказать, что обобщенный гармонический ряд сходится при 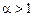и расходится при .

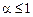Рассмотрим некоторые признаки сходимости рядов с положительными членами.

Признак Даламбера. Пусть для ряда с положительными членами

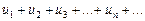(1)

существует предел отношения (n + 1)-го члена к n-му члену:

.

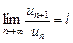Тогда если 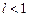, то ряд сходится, если 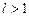, то ряд расходится.

(Если 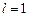, то вопрос о сходимости остается открытым.)

Доказательство этого признака основано на том, что если 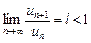, то члены ряда (1), начиная с некоторого, меньше соответствующих членов сходящейся геометрической прогрессии.

Пример. Исследовать сходимость ряда

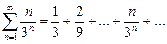
Вычислим предел

.

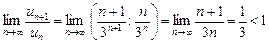По признаку Даламбера ряд сходится.

Признак Коши. Если для ряда с положительными членами

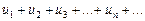(1)

величина 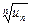имеет конечный предел при 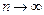, т.е.

,

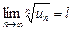то при 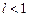ряд сходится, а при 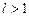ряд расходится.

Пример. Исследовать сходимость ряда

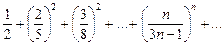
Применим признак Коши:

.

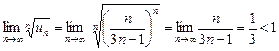Ряд сходится.