Функции Бесселя и Вебера. Рекуррентные соотношения для функций Бесселя.

Функции Бесселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:

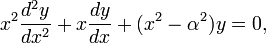
где 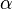— произвольное комплексное число, называемое порядком.

Наиболее часто используемые функции Бесселя — функции целых и полуцелых порядков.

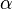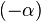Хотя и порождают одинаковые уравнения для вещественных 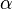, обычно договариваются о том, чтобы им соответствовали разные функции (это делается, например, для того, чтобы функция Бесселя была гладкой по ).

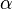Функции Бесселя впервые были определены швейцарским математиком Даниилом Бернулли, а названы в честь Фридриха Бесселя.

Функции Бесселя первого рода

Функциями Бесселя первого рода, обозначаемыми 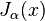, являются решения, конечные в точке 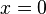при целых или неотрицательных 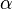. Выбор конкретной функции и её нормализации определяются её свойствами. Можно определить эти функции с помощью разложения в ряд Тейлора около нуля (или в более общий степенной ряд при нецелых ):

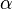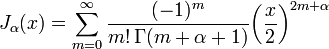
Здесь 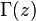— это гамма-функция Эйлера, обобщение факториала на нецелые значения. График функции Бесселя похож на синусоиду, колебания которой затухают пропорционально 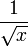, хотя на самом деле нули функции расположены не периодично.

Ниже приведены графики 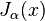для :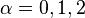

Если 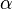не является целым числом, функци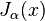и и 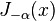линейно независимы и, следовательно, являются решениями уравнения. Но если 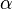целое, то верно следующее соотношение:

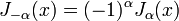
Оно означает, что в этом случае функции линейно зависимы. Тогда вторым решением уравнения станет функция Бесселя второго рода.

Можно дать другое определение функции Бесселя для целых значений 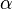, используя интегральное представление:

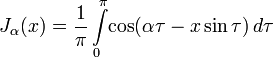
Этот подход использовал Бессель, изучив с его помощью некоторые свойства функций. Возможно и другое интегральное представление:

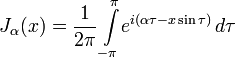
Функции Бесселя полуцелого порядка

Хотя в общем случае функции Бесселя не выражаются через элементарные функции, в частном случае полуцелого порядка это возможно:

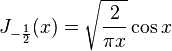
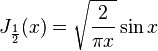
Остальные порядки могут быть получены с помощью рекуррентного соотношения:

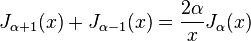
Функции Неймана (Функции Бесселя второго рода):

Функции Неймана — решения 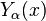уравнения Бесселя, бесконечные в точке .

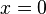Эта функция связана с 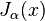следующим соотношением:

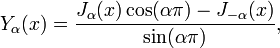
где в случае целого 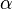берётся предел по 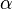, вычисляемый, например, с помощью правила Лопиталя.

Функции Неймана также называются функциями Бесселя второго рода. Линейная комбинация функций Бесселя первого и второго родов являет собой полное решение уравнения Бесселя:

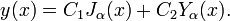
Ниже приведён график 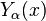для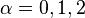

Асимптотика:

Для функций Бесселя первого и второго рода известны асимптотические формулы. При малых аргументах 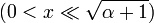и неотрицательных 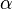они выглядят так:^[1]

,

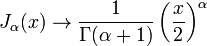
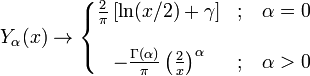где 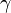— постоянная Эйлера — Маскерони (0.5772…), а 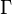— гамма-функция Эйлера. Для больших аргументов ( 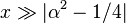) формулы выглядят так:

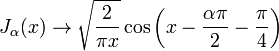
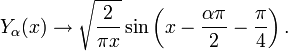
Гипергеометрический ряд

Функции Бесселя могут быть выражены через гипергеометрическую функцию:

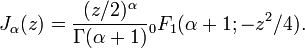
Таким образом, при целых 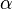функция Бесселя однозначная аналитическая, а при нецелых — многозначная аналитическая.

Производящая функция

Существует представление для функций Бесселя первого рода и целого порядка через коэффициенты ряда Лорана функции определённого вида, а именно

.
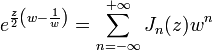