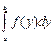Понятие интегральной суммы. Геометрический смысл.

Рассмотрим функцию f(x) определенную в каждой точке сегмента [a,b], a<b

Def Будем говорить, что задано разбиение сегмента [a,b] если заданы точки х_0, х_{1, ….,} х _{n, .}

Такие что а= х_0< х_1< х _2<….< х _n=b. { х _n }- разбиение х _n . Рассмотрим на сегменте [a,b] функцию f(x) принимающую в каждой точке сегмента конечные значения. По данному разбиению {x_k} построим d( х _к;x _к)= 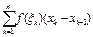(1)

x _кÎ[x_k-1;x_k] , полученное число называют интегральной суммой. Она зависит от способа разбиения Xk и от выбора точек x _к Отрезки получающиеся в результате разбиения [x_k-1;x_k] называются частичными отрезками. D х_к =х_к-х_к-1 – длина частичного отрезка

И тогда интегральную сумму (1) можно записать в виде d(х_к;x_к)= 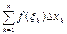(2)

Диаметр разбиения:максимальная длина частичного отрезка называется диаметром разбиения и обозначается числом d. d=maxD х_к

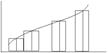
Геометрический смысл интегральных сумм:

F(x₁)*Dx₁=S прямоугольника 1

F(x₂)*Dx₂=S прямоугольника 2

f(x₁)*Dx₁+f(x₂)*Dx₂+…. f(xn)*Dx_n=d( х_к;x_к)=S*

где S* площадь ступенчатой фигуры, т.е. интегральная сумма (2) равна S* Если мы устремим диаметр d к 0, S* будет стремится к площади криволинейной трапеции, т.е. фигурой ограниченной снизу сегментом [a,b], сверху неотрицательной функцией f(x), с боков прямыми x=a, x=b.

x

Xo=a (x1) (X1) (x2) (X2) (x _{k-1 )} (xk) x_k (x_n-1) xn ( b=x_n)

Геом.смысл: s - сумма площадей прямоугольников с основаниями ÑХ1, ÑХ2,… Ñ Хn и высотами f (x₁), f(x₂)…f(x_n).

S*= f(x_k)* Ñ Хk. Т.о. интегральная сумма представляет собой

площадь ступенчатой фигуры. Но если d®0 (n ®¥), то

S* = f((x_k ; Xk) = f(x)dx = S криволин. трапеции

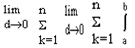Понятие определенного интеграла.

Def Если существует конечный предел I интегральных сумм s при l®0, то этот предел называется определенным интегралом от функции f(x) по отрезку [a,b] и обозначается I= =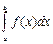

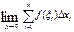
Def функция f(x) называется интегрируемой на [a,b] если для любой последовательности разбиений {Xk}, у которой 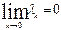соответствующая последовательность интегральных сумм {sk} стремится к одному и тому же числу I.

Def Число I называется определенным интегралом от функции f(x) оп отрезку [a,b], если для любого e>0 существует такое d>0, что при l<d (т.е. если отрезок [a,b] разбит на части с длинами DXi<d) независимо от выбора точек xI выполняется неравенство 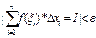, или же 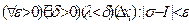для любого xiÎ[Xi-1, Xi]

Интегрируемость функции по Риману: Число I называется пределом интегральных сумм s, зависящих от (х_к;x_к) при d®0, если для любого положительного числа e, найдется соответствующее ему положительное число d, большее d, такое что для любого x_к будет выполняться |d (х_к;x_к)-I|<e. "e>0)($d=d(e)>0)(d<d) "x_k: |d (х_к;x_к)-I|<e Следует отметить, что существует только один предел s при d®0

I=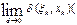

Функция f(x) называется интегрируемой по Риману на сегменте [a,b] если для этой функции на указанном сегменте существует I= 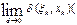при d®0

Число I называется определенным интегралом Римана от функции f(x) по сегменту [a,b] и обозначается так: I= 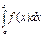, где а- нижний предел, b- верхний предел

Следует отметить, что 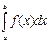= =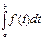