Решение задач 5,6 контрольной работы № 1

Задача 5. На множестве 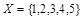задано бинарное отношение 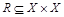: 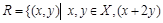делится на 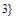. Представить отно-шение R различными способами; выяснить, какими свойствами оно обладает; является ли отношение R отношением эквивалентности или отношением порядка.

Решение. Отношение R можно задать перечислением всех элементов:

.

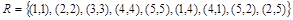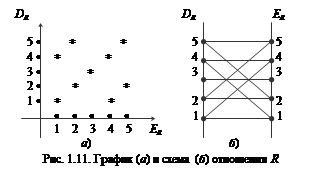
Наглядно представить отношение R можно с помощью графика (рис. 1.11, а), схемы (рис. 1.11, б), графа (рис. 1.12, а), матрицы отношения (рис. 1.12, б).

Выясним, какими свойствами обладает отношение.

Покажем, что отношение рефлексивно. При 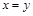условие “ 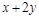делится на 3” принимает вид 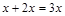– делится на 3 (выполняется при любых значениях ).

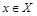Проверим, является ли отношение симметричным. Пусть 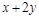делится на 3 (т.е. 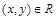). Составим пару 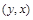и для нее проверим характеристическое свойство отношения:

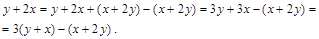
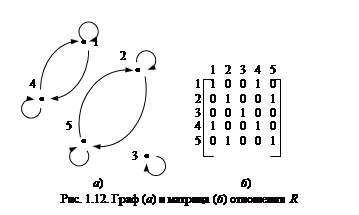Очевидно, что 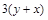делится на 3, а 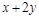делится на 3по условию, следовательно, 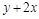делится на 3, т.е. 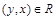. Отношение симметрично.

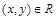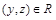Проверим, является ли отношение транзитивным. Пусть и , т.е. 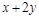делится на 3и 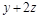делится на 3. Будет ли делиться на 3 выражение 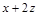, т.е. будет ли 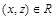? Преобразуем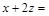 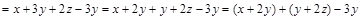делится на 3, т.к. первые два слагаемых делятся на 3 по условию и третье слагаемое 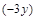делится на 3. Значит 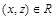, и отношение транзитивно.

Отношение R обладает свойствами рефлексивности, симметричности, транзитивности, следовательно, является отношением эквивалентности. На графе отношения R (рис. 1.12, а) хорошо видны классы эквивалентности – это подмножества {1,4}, {2,5}, {3} множества Х.

Задача 6. Дано множество 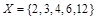и отношение 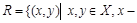делитель 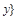. Показать, что отношение R является отношением порядка. Построить диаграмму Хассе частично упорядоченного множества 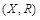. Существуют ли в множестве X наибольший и наименьший элементы? Существуют ли несравнимые элементы?

Решение. Покажем, что отношение R рефлексивно, антисимметрично и транзитивно.

Рефлексивность имеет место, так как любое число является своим делителем, т.е. .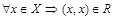

Пусть одновременно выполняются условия: 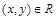и 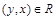. Тогда 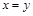. Действительно, 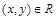означает, что x – делитель y, т.е. найдется целое число m такое, что 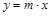. Одновременно найдется целое число n такое, что 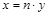. Отсюда 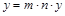и 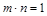. Последнее равенство выполняется пр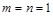и или 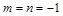, но все элементы множества X – положительные числа, и второй случай невозможен. Следовательно, 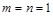, т.е. 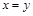, и отношение R антисимметрично.

Пусть 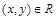и 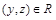, значит, найдутся 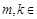Z такие, что 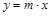, 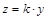. Тогда 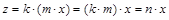, где 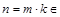Z. Следовательно, x является делителем z и 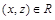. Отношение R транзитивно.

Отношение R рефлексивно, антисимметрично и транзитивно, т.е. является отношением порядка. Построим диаграмму Хассе частично упорядоченного множества 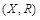. На нижнем (первом) уровне диаграммы поместим элементы 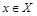, не имеющие других делителей, кроме себя ( 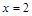и 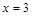). На втором уровне – элементы, не имеющие других делителей, кроме себя и элементов нижнего уровня ( 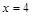и 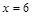). Оставшийся элемент 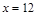делится на себя, на все элементы второго и первого уровней – помещаем его на третий уровень. Соединяем отрезком элементы соседних уровней, если элемент нижнего уровня является делителем элемента соседнего верхнего уровня. Диаграмма Хассе построена (рис. 1.13). Пара элементов 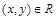тогда и только тогда, когда двигаясь по диаграмме только вверх, мы можем пройти от элемента x до элемента y.

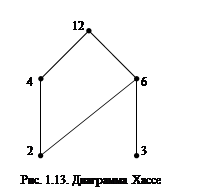По диаграмме Хассе легко обнаружить несравнимые элементы: 4 и 3; 2 и 3. Наибольшим элементом является 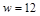(для всех 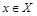выполнено условие “x является делителем 12”). Наименьшего элемента нет, но есть два минимальных: 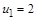и .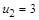

1.2.11. Контрольные вопросы и упражнения

1. Вставьте пропущенный знак “=” или “¹”:

{3,5} _____ {5,3}; (3,5) _____ (5,3).

2. Нарисуйте график декартова произведения 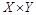, где 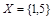, 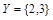. Совпадает ли он с графиком ?

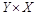3. Дайте определение бинарного отношения на множестве Х.

4. Обведите кружком номер правильного ответа:

Областью определения бинарного отношения R называется множество

1)

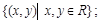
2)

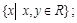
3)

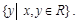
5. Найдите область определения и область значений отношения Q из примера 2 (п.п 1.2.2).

6. Какими способами можно задать бинарное отношение?

7. Нарисуйте график и схему отношения Р из примера 2 (см. 1.2.2).

8. Какое отношение является рефлексивным?

9. Какой особенностью обладает матрица рефлексивного отношения? А матрица симметричного отношения?

10. Вставьте пропущенное слово:

Отношение, обладающее свойствами рефлексивности, симметричности, транзитивности, называется отношением ________________ .

11. Запись 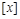используется для обозначения ________ _____________ .

12. Какое отношение называется отношением порядка?

13. Что такое частично упорядоченное множество?

14. Пусть R –отношение делимости. Какой порядок (частичный или линейный) задает это отношение на множестве 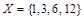? А на множестве 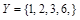? Построить диаграммы Хассе для 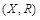и .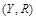

15. Что такое изоморфизм частично упорядоченных множеств? Изоморфны л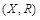и и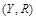

Реляционная алгебра