Определение бинарного отношения
Определение. Говорят, что на множестве X задано бинарное отношение R, если задано подмножество декартова произведения 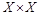 (т.е.
(т.е. 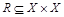 ).
).
Пример 2. Пусть 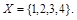 Зададим на Х следующие отношения:
Зададим на Х следующие отношения:
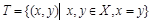 – отношение равенства;
– отношение равенства;
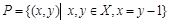 – отношение предшествования;
– отношение предшествования;
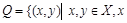 делится на
делится на 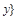 – отношение делимости.
– отношение делимости.
Все эти отношения заданы с помощью характеристического свойства. Ниже перечислены элементы этих отношений:
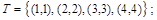
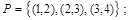
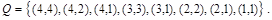
Тот факт, что пара ( x, y ) принадлежит данному отношению R,будем записывать: 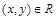 или xRy. Например, для отношения Q запись 4Q2 означает, что 4делится на 2 нацело, т.е.
или xRy. Например, для отношения Q запись 4Q2 означает, что 4делится на 2 нацело, т.е. 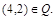
Областью определения 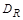 бинарного отношения R называется мно-жество
бинарного отношения R называется мно-жество 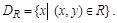
Областью значений 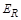 называется множество
называется множество 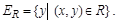
Так, для отношения Р из примера 2 областью определения является множество 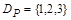 , а областью значений –
, а областью значений – 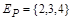 .
.
1.2.3. Способы задания бинарного отношения
Бинарное отношение можно задать, указав характеристическое свойство или перечислив все его элементы. Существуют и более наглядные способы задания бинарного отношения: график отношения, схема отношения, граф отношения, матрица отношения.
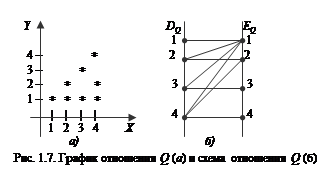
График отношения изображается в декартовой системе координат; на горизонтальной оси отмечается область определения, на вертикальной – область значений отношения; элементу отношения ( х,у ) соответствует точка плоскости с этими координатами. На рис. 1.7, а приведен график отношения Q примера 2.
Схема отношения изображается с помощью двух вертикальных прямых, левая из которых соответствует области определения отношения, а правая – множеству значений отношения. Если элемент ( х,у ) принадлежит отношению R, то соответствующие точки из 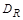 и
и 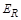 соединяются прямой. На рис. 1.7, б приведена схема отношения Q из примера 2.
соединяются прямой. На рис. 1.7, б приведена схема отношения Q из примера 2.
 |
Граф отношения 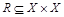 строится следующим образом. На плоскости в произвольном порядке изображаются точки – элементы множества Х. Пара точек х и у соединяется дугой (линией со стрелкой) тогда и только тогда, когда пара ( х,у ) принадлежит отношению R. На рис. 1.8, а приведен граф отношения Q примера 2.
строится следующим образом. На плоскости в произвольном порядке изображаются точки – элементы множества Х. Пара точек х и у соединяется дугой (линией со стрелкой) тогда и только тогда, когда пара ( х,у ) принадлежит отношению R. На рис. 1.8, а приведен граф отношения Q примера 2.
Матрица отношения 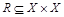 – это квадратная таблица, каждая строка и столбец которой соответствует некоторому элементу множества Х. На пересечении строки х и столбца у ставится 1, если пара
– это квадратная таблица, каждая строка и столбец которой соответствует некоторому элементу множества Х. На пересечении строки х и столбца у ставится 1, если пара 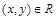 ; все остальные элементы матрицы заполняются нулями. Элементы матрицы нумеруются двумя индексами, первый равен номеру строки, второй - номеру столбца. Пусть
; все остальные элементы матрицы заполняются нулями. Элементы матрицы нумеруются двумя индексами, первый равен номеру строки, второй - номеру столбца. Пусть 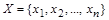 . Тогда матрица отношения
. Тогда матрица отношения 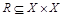 имеет n строк и n столбцов, а ее элемент
имеет n строк и n столбцов, а ее элемент 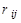 определяется по правилу:
определяется по правилу:
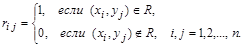
На рис.1.8, б приведена матрица отношения Q примера 2.
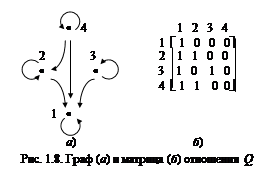 |
Свойства бинарных отношений
Бинарные отношения делятся на типы в зависимости от свойств, которыми они обладают. Рассмотрим следующие отношения на множестве 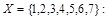
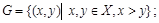
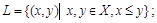
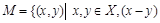 делится на
делится на 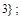
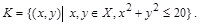
Отношение R на множестве Х называется рефлексивным,если для всех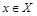 выполняется условие
выполняется условие 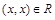 . Среди приведенных выше отношений рефлексивными являются отношение L (т.к. неравенство
. Среди приведенных выше отношений рефлексивными являются отношение L (т.к. неравенство 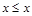 справедливо при всех
справедливо при всех 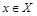 ) и отношение М (т.к. разность
) и отношение М (т.к. разность 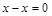 делится на 3, значит, пара
делится на 3, значит, пара 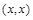 принадлежит отношению М при всех
принадлежит отношению М при всех 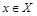 ).
).
Отношение R на множестве Х называется антирефлексивным, если условие 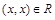 не выполняется ни при одном
не выполняется ни при одном 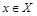 . Примером антирефлексивного отношения является отношение G (неравенство
. Примером антирефлексивного отношения является отношение G (неравенство 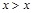 не выполняется ни при каких значениях х, следовательно, ни одна пара
не выполняется ни при каких значениях х, следовательно, ни одна пара 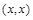 не принадлежит отношению G). Отметим, что отношение К не является рефлексивным
не принадлежит отношению G). Отметим, что отношение К не является рефлексивным 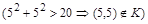 и не является антирефлексивным
и не является антирефлексивным 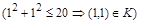 .
.
Отношение R на множестве Х называется симметричным, если из условия 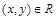 следует
следует 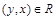 . Симметричными являются отношения М (если
. Симметричными являются отношения М (если 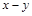 делится на 3, то и
делится на 3, то и 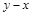 делится на 3) и К (если
делится на 3) и К (если 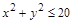 , то и
, то и 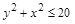 ).
).
Отношение R на множестве Х называется несимметричным, если для любых 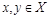 из условия
из условия 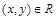 следует
следует 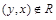 . Несимметричным является отношение G, т.к. условия
. Несимметричным является отношение G, т.к. условия 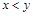 и
и 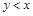 не могут выполняться одновременно (только одна из пар
не могут выполняться одновременно (только одна из пар 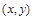 или
или 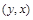 принадлежит отношению G).
принадлежит отношению G).
Отношение R на множестве Х называется антисимметричным, если для любых 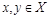 из условия
из условия 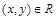 и
и 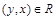 следует
следует 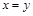 . Антисимметричным является отношение L, т.к. из одновременного выполнения
. Антисимметричным является отношение L, т.к. из одновременного выполнения 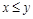 и
и 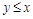 следует
следует 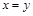 .
.
Отношение R на множестве Х называется транзитивным, если для любых 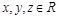 из одновременного выполнения условий
из одновременного выполнения условий 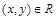 и
и 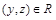 следует
следует 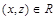 . Отношения G, L, M являются транзитивными, а отношение К нетранзитивно: если
. Отношения G, L, M являются транзитивными, а отношение К нетранзитивно: если 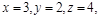 то
то 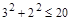 и
и 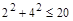 , но
, но 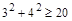 , то есть выполняются условия
, то есть выполняются условия 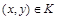 и
и 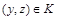 , но
, но 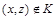 .
.
Отношения эквивалентности
Рассмотрим три отношения: M, S, H. Отношение М описано в 1.2.4. Отношение S введем на множестве X всех треугольников следующим образом: этому отношению принадлежат пары треугольников такие, что площадь треугольника x равна площади треугольника y.
Отношение Н действует на множестве жителей г. Томска и содержит пары 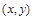 такие, что х и у носят шляпы одинакового размера.
такие, что х и у носят шляпы одинакового размера.
Свойства этих трех отношений приведены в таблице 1.3, где Р означает рефлексивность, АР – антирефлексивность, С – симметричность, АС - антисимметричность, НС – несимметричность, Т – транзитивность отношения. В качестве упражнения проверьте правильность заполнения таблицы, пользуясь определениями свойств бинарных отношений.
Таблица 1.3
Свойства отношений
| Отношение | Р | АР | С | АС | НС | Т |
| М | + | - | + | - | - | + |
| S | + | - | + | - | - | + |
| H | + | - | + | - | - | + |
Мы видим, что отношения обладают одинаковыми свойствами, поэтому их относят к одному типу.
Определение. Отношение R на множестве Х называется отношением эквивалентности, если оно обладает свойствами рефлексивности, симметричности, транзитивности.
Таким образом, отношения M, S, H являются отношениями эквивалентности на соответствующих множествах Х. Важной особенностью отношений эквивалентности является то, что они разбивают все множество Х на непересекающиеся подмножества – классы эквивалентности.
Определение. Классом эквивалентности, порожденным элементом 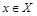 , называется подмножество
, называется подмножество 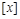 множества Х, для элементов которого выполняется условие
множества Х, для элементов которого выполняется условие 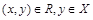 . Таким образом, класс эквивалентности
. Таким образом, класс эквивалентности 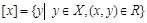 .
.
Так, отношение М разбивает множество 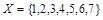 на три класса эквивалентности:
на три класса эквивалентности: 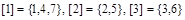 . Класс, порожденный элементом 4, совпадает с классом [1]; [5] = [2], [3] = [6], [7] = [1].
. Класс, порожденный элементом 4, совпадает с классом [1]; [5] = [2], [3] = [6], [7] = [1].
Классы эквивалентности образуют систему непустых непересекающихся подмножеств множества Х, в объединении дающую все множество Х – т.е. образуют разбиение множества Х (см. 1.1.6).
Отношение эквивалентности обозначают “ º “, поэтому определение класса эквивалентности можно записать так: 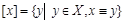 .
.
Множество различных классов эквивалентности множества X по отношению R называется фактор-множеством и обозначается 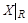 . Так, для отношения M фактор-множество состоит из трех элементов:
. Так, для отношения M фактор-множество состоит из трех элементов:
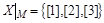 .
.
Теорема 1. Пусть R – отношение эквивалентности на множестве X и 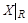 - совокупность всех различных классов эквивалентности по отношению R. Тогда
- совокупность всех различных классов эквивалентности по отношению R. Тогда 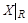 - разбиение множества X.
- разбиение множества X.
Доказательство. По условию теоремы R – отношение эквивалентности, т.е. рефлексивно, симметрично и транзитивно. Покажем, что 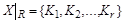 - разбиение множества X, т.е.
- разбиение множества X, т.е.
а) 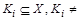 Æ;
Æ;
б) 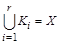 ;
;
в) 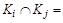 Æ,
Æ, 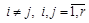 .
.
Условие а выполняется по определению класса эквивалентности и по свойству рефлексивности, т.к. 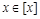 для любого
для любого 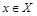 .
.
Условие б выполняется, так как каждый элемент множества X попадает в какой-либо класс эквивалентности и 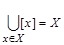 .
.
Условие в докажем методом “от противного”. Пусть 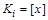 и
и 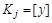 - разные классы эквивалентности (т.е.
- разные классы эквивалентности (т.е. 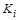 и
и 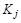 отличаются хотя бы одним элементом). Покажем, что они не пересекаются. Предположим противное: найдется элемент
отличаются хотя бы одним элементом). Покажем, что они не пересекаются. Предположим противное: найдется элемент 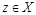 такой, что
такой, что 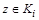 и
и 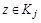 . По определению класса эквивалентности
. По определению класса эквивалентности 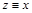 и
и 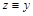 . По свойствам симметричности и транзитивности отношения R имеем:
. По свойствам симметричности и транзитивности отношения R имеем: 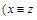 и
и 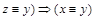 - отсюда следует равенство множеств
- отсюда следует равенство множеств 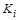 и
и 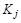 .
.
Действительно, возьмем произвольный элемент 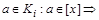
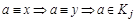 в силу произвольности a следует
в силу произвольности a следует 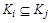 . Возьмем произвольный элемент
. Возьмем произвольный элемент 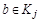 :
: 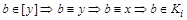 - в силу произвольности b следует
- в силу произвольности b следует 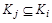 . По определению равенства множеств
. По определению равенства множеств 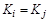 .
.
Условие в доказано: если классы эквивалентности не совпадают, то они не пересекаются.
Следовательно, фактор-множество 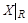 является разбиением множества X.
является разбиением множества X.
Теорема 2. Всякое разбиение множества X порождает на X отношение эквивалентности.
Доказательство. Пусть 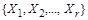 - разбиение множества X. Рассмотрим на X отношение
- разбиение множества X. Рассмотрим на X отношение 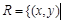 найдется
найдется 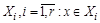 и
и 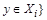 .
.
Покажем, что R – отношение эквивалентности.
Рефлексивность отношения R следует из условия 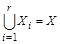 . Каждый элемент множества X попадает в одно из множеств
. Каждый элемент множества X попадает в одно из множеств 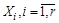 , поэтому
, поэтому 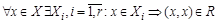 .
.
Покажем, что отношение R симметрично. Пусть 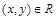 . Это означает, что
. Это означает, что
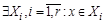 и
и 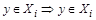 и
и 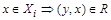 .
.
Покажем, что R транзитивно. Пусть 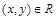 и
и 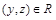 . Тогда найдется множество
. Тогда найдется множество 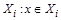 и
и 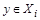 и множество
и множество 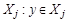 и
и 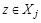 . Но так как различные блоки разбиения не пересекаются, а
. Но так как различные блоки разбиения не пересекаются, а 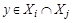 , то
, то 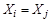 . Следовательно,
. Следовательно, 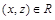 и R транзитивно.
и R транзитивно.
Отношение R обладает свойствами рефлексивности, симметричности, транзитивности, т.е. является отношением эквивалентности. Теорема доказана.
Отношения порядка
Рассмотрим отношения G, L из 1.2.4, отношение Q из 1.2.2 и отношение включения V на множестве всех подмножеств целых чисел (B(Z) – булеан множества Z): 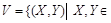 B(Z)
B(Z) 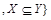 .
.
Таблица 1.4
Свойства отношений
| Отношение | Р | АР | С | АС | НС | Т |
| G | - | + | - | - | + | + |
| L | + | - | - | + | - | + |
| Q | + | - | - | + | - | + |
| V | + | - | - | + | - | + |
Мы видим, что по свойствам эти отношения разделились на два типа.
Определение. Отношение R на множестве Х, обладающее свойствами рефлексивности, антисимметричности, транзитивности, называется отношением порядка на множестве Х (обозначается “p”).
Определение. Отношение R на множестве Х, обладающее свойствами антирефлексивности, несимметричности, транзитивности, называется отношением строгого порядка.
Таким образом, отношения L, Q, V являются отношениями порядка на соответствующих множествах, а отношение G – отношением строгого порядка.
