Геометрические фигуры в пространстве

С пространственными геометрическими фигурами (куб, шар, параллелепипед и др.) дети знакомятся в практической деятельнос­ти (при конструировании, во время игры) гораздо раньше, чем с плоскими фигурами. Особенности мышления младших дошкольни­ков определяют выбор наглядного материала. В этом возрасте важ­но, чтобы изучаемый объект был крупный, яркий, чтобы им можно было выполнять действия (поиграть). Обследование идет на сенсор­ной основе, поэтому с моделями объемных фигур детям знакомить­ся легче. Кубики, шарики, бруски и др. входят в игру детей одно­временно с первыми игрушками. Обычно математические названия им не даются, но идет знакомство с различными объемными фор­мами, а в речь вводятся только некоторые термины.

Основными фигурами в пространстве считаются: точка, прямая, плоскость. На каждой плоскости выполняются все утверждения планиметрии. В стереометрии, так же как в планиметрии, вводится ряд аксиом, которые изучаются в школьном курсе геометрии.

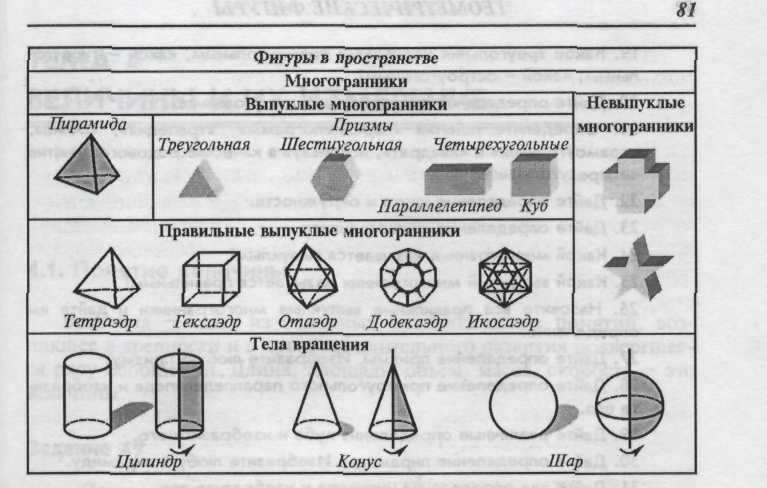
Объемные геометрические фигуры называют геометрическими телами. В пространстве выделяют многогранники (призма, пирамида и др.) и тела вращения (шар, конус, цилиндр и др.).

Многогранники

Многогранник- это ограниченное тело, поверхность которого состоит из конечного числа многоугольников. Эти многоугольники называются гранями, их стороны — ребрами, а вершины - вершина­ми многогранника.

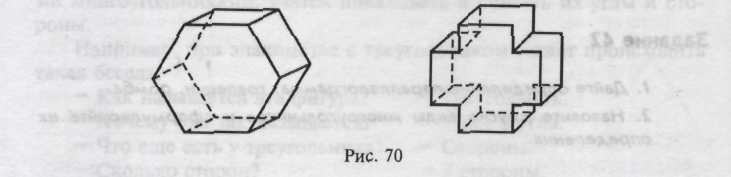
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости любой его грани (рис. 70).

Выпуклый многогранник невыпуклый многогранник

Задание 43

Покажите вершины, ребра и грани многогранников, изображен­ных на рисунке 70. Какими геометрическими фигурами они явля­ются!

Правильный выпуклый многогранник имеет грани - правильные равные многоугольники, и в каждой его вершине сходится одинако­вое число ребер.

Задание 44

1. Вспомните, какие фигуры называют равными.

2. Назовите известные вам правильные выпуклые многогранники.

Всего существует 5 правильных многогранников, в отличие от правильных многоугольников, которых бесконечно много. Это об­условлено двумя причинами:

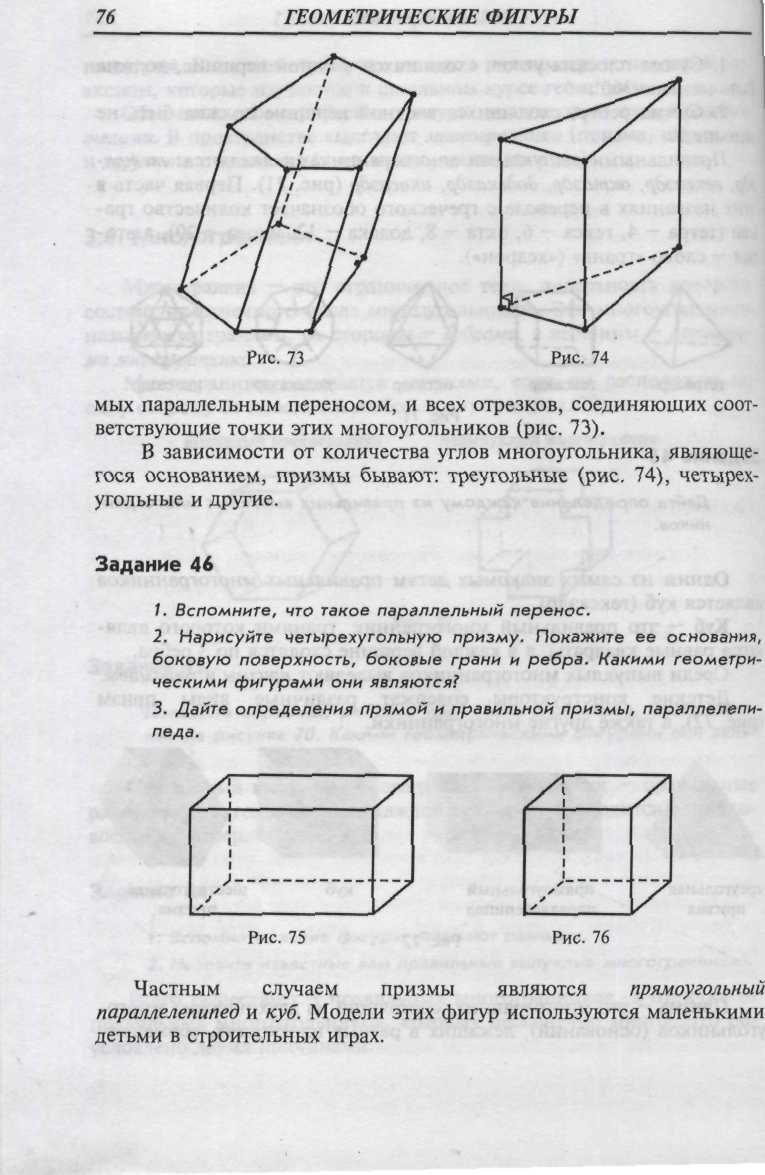
Прямоугольный параллелепипед - это параллелепипед, все грани которого прямоугольники (рис. 75).

Куб — это прямоугольный параллелепипед с равными ребрами (или все грани которого являются квадратами) (рис. 76).

Дошкольники, изучая куб, могут отметить, что его поверхность состоит из шести квадратов, что у него 8 вершин. Свойства куба осваиваются ими, например, при выполнении такого задания: «Обклей кубик цветной бумагой. Что для этого нужно?» (вырезать 6 одинаковых квадратов).

Прямоугольный параллелепипед в детском саду часто называют «кирпичиком» или «бруском», что допустимо в предматематической подготовке. Эти слова являются предэталонными названиями гео­метрических фигур, так же как «кубик», «крыша» (треугольная при­зма), «столбик» (цилиндр) и др.

Младшим школьникам можно предложить задание: «Вырежи выкройку для коробки. Какую форму имеет каждая часть?» Таким образом, дети выясняют, что гранями прямоугольного параллелепи­педа являются прямоугольники, не формулируя этого явно.

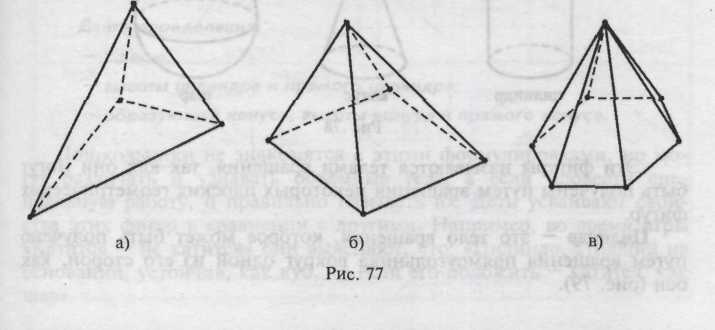
Пирамида — многогранник, состоящий из плоского многоугольника (основания), точки, не лежащей в плоскости основания (вершины), и всех отрезков, соединяющих вершину пирамиды с точками основания (рис. 77). Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. Поверхность пирамиды состоит из основания и боковых граней. Все боковые граны — треугольники.

В зависимости от числа углов многоугольника, являющегося основанием, пирамиды бывают: треугольные (рис. 77а), четырех­угольные (рис. 776), пятиугольные и другие пирамиды.

Любая грань треугольной пирамиды может служить ее основани­ем. Это же название носит и правильный многогранник, тетраэдр, гранями которого являются равные равносторонние треугольники.

Форму тетраэдра имеет пакет молока (старой упаковки), а еги­петские пирамиды имеют форму четырехугольной правильной пи­рамиды. Дошкольники называют «пирамидкой» совсем другую мо­дель — игрушку из колец разной величины, которая имеет форму конуса. Эта ситуация может вызвать затруднения в запоминании и правильном применении геометрических терминов у детей. Данная проблема преодолевается при своевременном грамотном объясне­нии и разделении названий игрушек от названий их формы, этало­нами для определения которой служат геометрические фигуры.

Задание 47

1. Нарисуйте пятиугольную пирамиду. Покажите ее основание, бо­ковую поверхность, боковые грани и ребра. Какими геометриче­скими фигурами они являются?

2. Дайте определения высоты пирамиды и правильной пирамиды.

Тела вращения

Изучая форму окружающих предметов, дошкольники сталкива­ются с телами вращения (рис. 78).

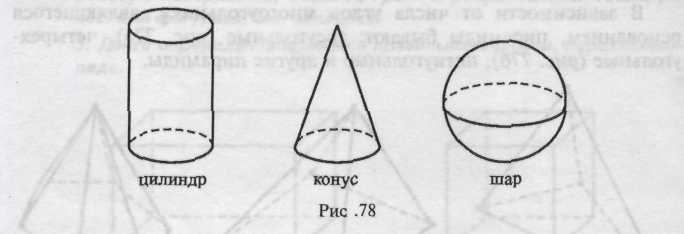
Эти фигуры называются телами вращения, так как они могут быть получены путем вращения некоторых плоских геометрических фигур.

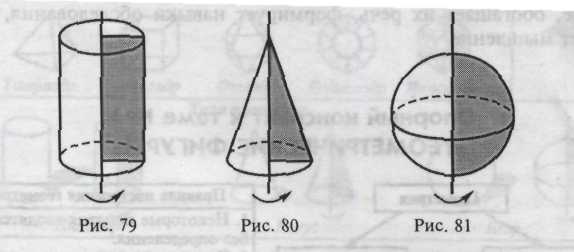
Цилиндр - это тело вращения, которое может быть получено путем вращения прямоугольника вокруг одной из его сторон, как оси (рис. 79).

Конус — это тело вращения, которое может быть получено путем вращения прямоугольного треугольника вокруг одного из его кате­тов, как оси (рис. 80),

Шар — это тело вращения, которое может быть получено путем вращения половины круга вокруг его диаметра, как оси (рис. 81).

Определения этих фигур из курса геометрии средней школы:

Цилиндр - тело, которое состоит из двух кругов (оснований), совмещаемых параллельным

переносом, и всех отрезков, соединяющих

соответствующие точки этих кругов.

Конус - тело, которое состоит из круга (основания), точки (вер­шины), не лежащей в плоскости этого круга, и всех отрезков, сое­диняющих вершину конуса с точками основания.

Шар— тело, которое состоит из всех точек пространства, нахо­дящихся на расстоянии не более заданного (радиуса) от данной точ­ки (центра).

Задание 48

Дайте определения:

— сферы;

— высоты цилиндре и прямого цилиндра;

— образующей конуса, высоты конуса и прямого конуса.

Дошкольники не знакомятся с этими формулировками, но мо­гут различать и узнавать объемные тела, а если провести спе­циальную работу, и правильно называть их. Дети усваивают свой­ства этих фигур в сравнении с другими. Например, во время игры «Катится — не катится» они выясняют, что: «Цилиндр, стоящий на основании, устойчив, как куб, но если его положить - катится, как шар».

Обследование поверхности дает знание того, что основанием цилиндра и конуса является круг. Рисование объемных предметов разной формы на плоскости учит детей сравнивать, проводить ана­логию, моделировать, трансформировать пространство на плоскос­ти. Например, в процессе обсуждения таких вопросов: «Какой фор­мы мяч? Какую фигуру надо нарисовать, чтобы изобразить мяч?»

Знакомство с объемными фигурами расширяет знания детей об окружающем мире, закладывает основы для изучения геометрии в школе, обогащает их речь, формирует навыки обследования, раз­вивает мышление.

Вопросы для самоконтроля к теме № 3

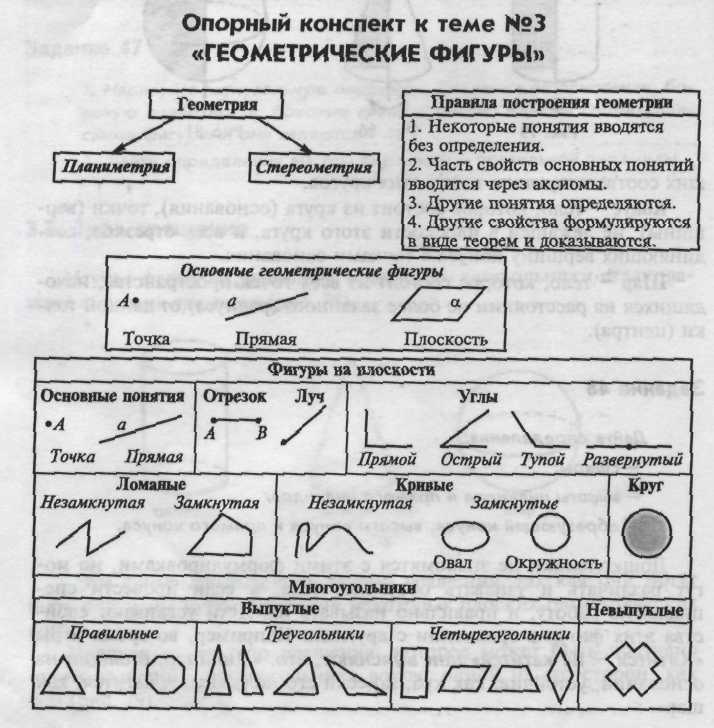
1. Что изучает геометрия?

2. Что изучает планиметрия?

3. Что изучает стереометрия?

4. Что называется геометрической фигурой?

5. Назовите правила построения геометрии.

6. Назовите основные фигуры на плоскости и в пространстве.

7. Какие фигуры называются плоскими?

8. Какие фигуры называются выпуклыми?

9. Дайте определение отрезка.

10. Дайте определение луча.

11. Дайте определение угла.

12. Какая линия называется ломаной?

13. Какая ломаная называется простой?

14. Дайте определение многоугольника.

15. Какой многоугольник называется выпуклым?

16. Какой многоугольник называется правильным?

17. Дайте определение треугольника.

18. Какой треугольник называется равносторонним, какой — равно­бедренным, какой - разносторонним?

ТЕМА 4

ВЕЛИЧИНЫ И ИХ ИЗМЕРЕНИЕ

Понятие величины

Величина - одно из основных математических понятий, воз­никшее в древности и в процессе длительного развития подвергшее­ся ряду обобщений. Длина, площадь, объем, масса, скорость - это величины.

Задание 49

Приведите примеры различных величии, изучаемых в школе на уроках математики, физики, химии. Вспомните способы их изме­рения и единицы этих величин.

Величины представляют собой особые свойства реальных пред­метов или явлений, которые проявляются при сравнении их по это­му свойству, причем каждая величина связана с определенным спо­собом сравнения. Например, длину отрезков можно сравнить спо­собом наложения, а массу предметов - взвешиванием. Величины можно оценивать количественно на основе сравнения.

Величину рассматривают как обобщение свойств некоторых объектов и как индивидуальную характеристику свойства конкрет­ного объекта. Например, свойство предметов «иметь протяжен­ность» называется «длиной».

Однородные величины - величины, которые выражают одно и то же свойство объектов некоторого класса. Например, длина, шири­на, периметр — однородные величины.

Разнородные величины выражают различные свойства объектов (один предмет может иметь массу, объем и др.).

Свойства однородных величин

1. Однородные величины можно сравнивать. Для любых величин А и В справедливо только одно из отношений: А<В, А>В, А=В.

Например, масса книги больше массы карандаша, а длина ка­рандаша меньше длины стола.

2. Однородные величины можно складывать и вычитать. В резуль­тате получается величина того же рода.

Величины, которые можно складывать, называются аддитивны­ми. Например, можно складывать длины предметов. В результате получается длина. Существуют величины, которые не являются ад­дитивными, например температура. При соединении воды разной температуры из двух сосудов получается смесь, температуру которой нельзя определить сложением величин.

Мы будем рассматривать только аддитивные величины.

Пусть: А — длина ткани,

В — длина куска, который отрезали, тогда;

(А—В) - длина оставшегося куска.

3. Величину можно умножать и делить на положительное дей­ствительное число. В результате получается величина того же рода.

Примеры.

1) «Налей в банку 6 стаканов воды». Если объем воды в стака­не — V, то объем воды в банке .

2) «Раздели ленту на 4 равные части». Если длина ленты — L, то длина каждой ее части — L.4.

4.Однородные величины можно делить. В результате получается положительное действительное число, его называют отношением ве­личин. А:В=х о А—В-х.

Пример,

«Сколько ленточек длиной В можно получить из ленты длиной А?», (х = А:В, где х - отношение величин А и В).

5. Величину можно оценить количественно, то есть измерить.

Дети уже в дошкольном возрасте учатся выделять разные пара­метры размера предмета (длину, ширину, высоту), сравнивать пред­меты по этим параметрам (наложением и приложением), измерять протяженность условными мерками. Довольно рано происходит знакомство с площадью фигур, объемом жидких и сыпучих веществ, массой физических тел, промежутками времени. В быту дети накап­ливают необходимый опыт для последующего обучения, системати­зации и расширения знаний. Измерительная деятельность формиру­ется только под воздействием целенаправленного обучения. В на­чальной школе происходит знакомство с общепринятыми единицами величин (метром, литром, килограммом и др.).

Измерение величин

Сравнивая величины непосредственно, можно установить их равенство или неравенство.

Для получения более точного результата сравнения величины измеряют. Например, измеряя массу арбуза на чашечных весах, сравнивают ее с массой гири. Измеряя длину комнаты шагами, сравнивают ее с длиной шага.

Процесс сравнения зависит от рода величины: длину измеряют с помощью линейки, массу — используя весы. Каким бы ни был этот процесс, в результате измерения получается определенное чис­ло, зависящее от выбранной единицы величины.

Измерение заключается в сравнении данной величины с некото­рой величиной того же рода, принятой за единицу.

Цель измерения — получить численную характеристику данной величины при выбранной единице величины.

Измерить величину А — это значит найти такое положительное действительное число х, что А=х Е, где Е — величина того же рода, принятая за единицу. Число х называют численным значением вели­чины А при единице величины Е.

Численное значение величины показывает, во сколько раз за­данная величина больше или меньше величины, принятой за еди­ницу.

Примеры.

1) Если масса дыни 3 кг, то 3 — численное значение массы дыни при единице массы килограмм.

2) Если длина отрезка 10 см, то 10 - численное значение длины отрезка при единице длины сантиметр.

Величины, определяемые одним численным значением, называ­ются скалярными (длина, объем, масса и др.). Существуют еще век­торные величины, которые определяются численным значением и направлением (скорость, сила и др.). Мы будем рассматривать толь­ко скалярные величины (длину, площадь, объем, массу, время).

Значение измерения очень велико. Не всегда можно сравнить или сложить (вычесть) величины непосредственно (например, дли­ну дорог). Измерение позволяет свести сравнение величин к сравне­нию чисел, а действия с величинами — к действиям над числами, что значительно проще.