Сферически симметричное решение уравнения Гельмгольца

В ограниченной области

При поиске сферически симметричных решений уравнениеГельмгольца в сферических координатах сводится к обыкновенному дифференциальному уравнению

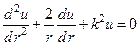(17)

Умножив все члены уравнения на r, после некоторых преобразований получим

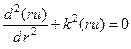(18)

Общее решение этого уравнения для функции ru хорошо известно, а тогда можно записать и общее решение уравнения (1) при .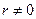

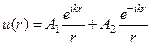, (19)

где А₁ и А₂ произвольные постоянные, которые определяются из граничного условия. При решении внутренней краевой задачи решение ищется внутри сферы 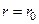, где оно должно быть регулярным. Для выполнения этого условия необходимо положить 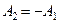. Это условие оказывается и достаточным. Действительно, прямым дифференцированием и применением правила Лопиталя можно убедиться, что при этом решение (19) будет регулярно. Таким образом, решение задачи имеет вид

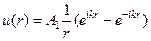(20)

Сферически симметричное решение уравнения Гельмгольца

Для неограниченной области

Теперь будем решать для уравнения (17) внешнюю неоднородную краевую задачу с условием на поверхности сферы радиуса r₀.

Если k² является целым положительным числом, то для вещественных решений уравнения (1) будем иметь

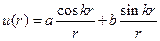(21)

В случае внешней краевой задачи решение (4) регулярно во всей бесконечной области 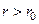, где r₀ – граница области. Произвольные постоянные a и b определяются из граничных условий, но при этом представляют бесчисленное множество. Следовательно, внешняя граничная задача имеет бесчисленное множество регулярных решений, обращающихся в нуль на бесконечности.

Чтобы разобраться в физическом смысле полученного решения напомним, что к уравнению (17) можно прийти в результате применения метода разделения переменных к волновому уравнению

,

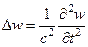причем с² и k² связаны соотношением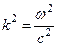

Решение этого уравнения можно получить, если умножить общее решение (19) на e ^–iωt, что приведет к выражению

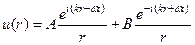(22)

Подставив сюда значение 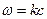и приняв во внимание, что числа А и В комплексны, найдем, что вещественная часть этого выражения может быть представлена в виде

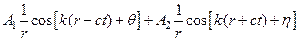(23)

где А₁ и В₁ – произвольные постоянные,

Выражение (23) описывает сумму двух сферических волн. Рассмотрим сначала первое слагаемое. Представим выражение под знаком косинуса следующим образом

,

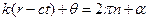где n – целое число и .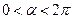

Каждому значению разности 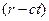соответствуют свои значения n и α. Число α называют фазой волны. Геометрическое место точек одинаковой фазы представляют систему концентрических сферических поверхностей. На каждой из них выражение 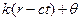остается постоянным. Следовательно, их радиус r должен расти со скоростью с. Таким образом, первое слагаемое представляет собой систему волн, расходящихся от поверхности 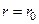, на которой заданы граничные условия.

Аналогичным образом можно установить, что второе слагаемое суммы (23) представляет собой систему сходящихся волн, которые со скоростью с приходят из бесконечности к поверхности .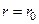

С физической точки зрения, расходящиеся волны имеют своим источником поверхность 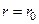. В то же время сходящиеся волны не имеют физического смысла, поскольку для них источник отсутствует. Следовательно, как в выражении (22), так и в выражении (19) предыдущего параграфа, мы должны оставить только первый член.

Чтобы найти аналитический признак, позволяющий отобрать решения уравнения Гельмгольца, соответствующие только расходящимся волнам, мы рассмотрим функци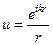и

и ,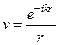

которые входят в общее решение (19), причем, как мы установили, расходящимся волнам соответствует только первая из них. Продифференцируем эти функции по r, установим, что они удовлетворяют следующим дифференциальным соотношениям

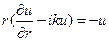и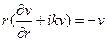

Устремив теперь r к бесконечности и помня о том, что должны выполняться условия

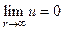и ,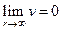

мы придем к следующим предельным соотношениям

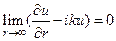и ,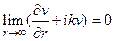

При этом легко убедиться, что функция v первому условию не удовлетворяет.

Итак, аналитический признак того, что решение соответствует расходящимся волнам. состоит из двух условий

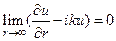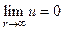и (24)

Поскольку любые расходящихся волн на большом удалении от источника будут обладать теми же закономерностями, что и сферические расходящиеся волны, то и для них должны выполняться соотношения (24). Эти условия были впервые установлены Зоммерфельдом и получили название условия излучения. Выполнение этих условий обеспечивает единственность решения внешней краевой задачи для уравнения Гельмгольца, т.е. они играют ту же роль, что и условие обращения в нуль на бесконечности в задачах для уравнения Лапласа.

Г л а в а IX. Уравнения теории упругости

В этой главе мы покажем, как системы уравнений теории упругости и уравнений электромагнитного поля сводятся к волновым уравнениям в результате введения в рассмотрение скалярного и векторного потенциала.