Решение дифференциального уравнения

ТИПА "ВХОД-ВЫХОД"

Мы будем рассматривать дифференциальные уравнения с постоянными коэффициентами. В связи с этим уравнению (1.11) можно придать более конкретный вид

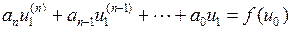, (1.24)

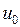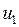где величины и – функции времени 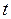, а коэффициенты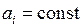

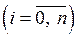
Выражение (1.24) называется неоднородным дифференциальным уравнением n-го порядка. Его решение равно сумме общего решения 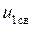однородного уравнения

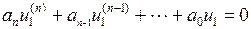(1.25)

и какого-либо частного решения 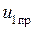неоднородного уравнения (1.24)

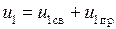. (1.26)

В электротехнике решение 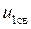называется свободной составляющей и представляет собой сигнал на выходе четырехполюсника при скачкообразном изменении правой части 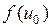уравнения (1.24) до нуля; решение 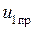носит название принужденной составляющей и соответствует сигналу на выходе четырехполюсника в установившимся режиме, ее состав зависит только от структуры .

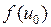1.7.1. ОБЩЕЕ РЕШЕНИЕ ОДНОРОДНОГО УРАВНЕНИЯ

(СВОБОДНОЕ ДВИЖЕНИЕ СИСТЕМЫ)

Общее решение однородного уравнения (1.25) состоит из совокупности частных решений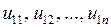

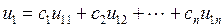, (1.27)

где 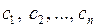– произвольные постоянные.

Поскольку экспоненциальная функция является собственной функцией линейной системы, то частные решения следует искать в виде

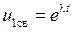. (1.28)

Подставляя (1.28) в (1.25) получим

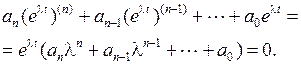(1.29)

Поскольку 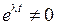, то уравнение (1.29) удовлетворяется лишь при выполнении следующего равенства:

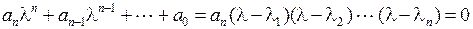. (1.30)

Из уравнения (1.30) видно, что решениями однородного уравнения могут быть экспоненты с показателями 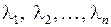, поскольку для каждого из них 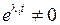, но в (1.30) найдется сомножитель 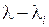, равный нулю при 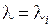. Следовательно, уравнение (1.30) определяет число и вид частных решений уравнения (1.25), в связи с чем и носит название характеристического, а 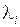называются корнями характеристического уравнения.

A. Корни характеристического уравнения

действительные и разные

В этом случае частные решения имеют следующий вид:

,

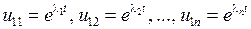а общее решение уравнения (1.25) в соответствии с (1.27) запишется следующим образом:

.

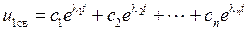Пример 1.5. Определить вид свободного решения однородного уравнения .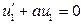

Характеристическое уравнение имеет следующий вид:

.

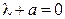Корень 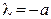. Тогда общее решение уравнения состоит из одного частного решения

.

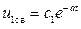Б. Корни характеристического уравнения комплексные

Поскольку коэффициенты 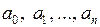в (1.30) действительные, то каждому комплексному корню 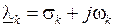обязательно соответствует сопряженный корень 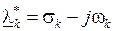. Здесь символ " 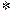" означает сопряжение. Этим корням соответствуют частные решения

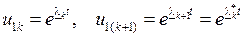. (1.31)

В общее решение уравнения (1.25) они вносят следующий вклад:

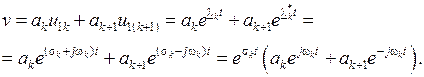
Применяя формулу Эйлера к комплексным экспонентам

,

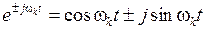получим, что

.

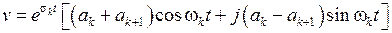Поскольку уравнение (1.25) с действительными коэффициентами, то его решение также является вещественной функцией. Поэтому сумма коэффициентов должна дать вещественное число, а разность – мнимое число. Отсюда следует, что частные решения вида (1.31) могут быть заменены решениями вида

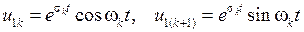, (1.32)

а общее решение может быть записано следующим образом:

.

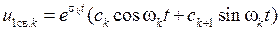Пример 1.6. Определить вид свободного решения однородного уравнения .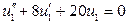

Характеристическое уравнение имеет вид

.

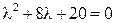Корни

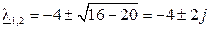
согласно (1.32) обусловливают частные решения

.

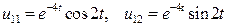Тогда общее решение уравнения равно

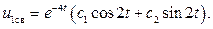
В. корни характеристического уравнения

вещественные и кратные

Пусть среди корней характеристического уравнения есть корень 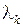кратности 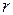. Ему соответствуют 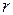частных решений вида

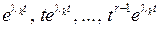. (1.33)

Тогда решение уравнения (1.25) содержит в себе составляющую вида

.

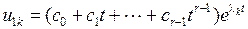Пример 1.7. Определить вид свободного решения однородного уравнения

.

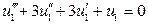Характеристическое уравнение имеет вид

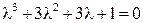
или

.

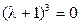Корню 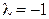кратности 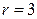соответствуют частные решения

.

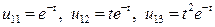Согласно (1.33) общее решение уравнения будет иметь вид

.

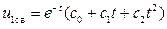1.7.2. ЧАСТНОЕ РЕШЕНИЕ НЕОДНОРОДНОГО

ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

(ПРИНУЖДЕННЫЙ РЕЖИМ СИСТЕМЫ)

Пусть 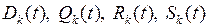– многочлены степени .

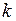1. Если правая часть уравнения (1.24) имеет вид

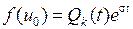, (1.34)

то его частное решение ищется в виде

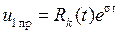, (1.35)

если 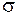не является корнем характеристического уравнения, или в виде

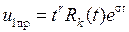, (1.36)

если 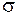является r-кратным корнем характеристического уравнения (1.25).

2. Если

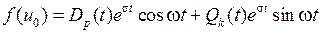, (1.37)

то частное решение ищется в виде

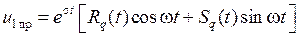, (1.38)

если 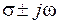не является корнем характеристического уравнения (1.25), или в виде

,

если 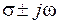является r-кратным корнем характеристического уравнения системы. Здесь .

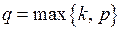Во всех случаях 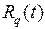и 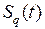– многочлены с неопределенными постоянными. Кроме того, если правая часть уравнения (1.24) представлена комбинацией функций (1.34), (1.35) и (1.37), (1.38), то частное решение равно сумме решений, соответ­ствующих каждому члену линейной комбинации.

Пример 1.8. Определить принужденное решение уравнения .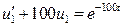

Корень характеристического уравнения 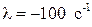. Он совпадает с коэффициентом затухания экспоненты в правой части уравнения. Согласно (1.36)

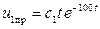. (1.39)

Коэффициент 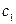найдем, подставив (1.39) в исходное уравнение

.

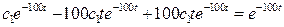Отсюда 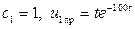.