Решение уравнения (1) имеет вид

Физика колебаний и волн. Квантовая физика

Конспект лекций для 3 семестра изучения курса «Физика»

Омск 2007

УДК 530+534.1+535(075)

ББК 22.314+22.343+22.336я73

Д 18

Рецензенты:

Машков Ю.К., докт. техн. наук, проф., зав. каф. физики СибАДИ,

Полещенко К.Н., докт. техн. наук, проф. каф. педагогических информационных технологий и дополнительного образования ОмГУ.

Д 18 Данилов, С.В., Егорова, В.А., Кропотин, О.В. Физика колебаний и волн. Квантовая физика: учеб. пособие. 2 –е изд. перераб./ Сост. С.В. Данилов, В.А. Егорова, О.В. Кропотин. – Омск : Изд-во ОмГТУ, 2007. – 64 с.

Приведены программа и контрольные задания. Изложение материала соответствует курсу общей физики, изучаемому в вузе.

Для студентов заочной и очно-заочной форм обучения.

Печатается по решению редакционно-издательского совета

Омского государственного технического университета.

УДК 530+534.1+535(075)

ББК 22.314+22.343+22.336я73

© Авторы, 2007

© Омский государственный

технический университет, 2007

ПРОГРАММА

1. Колебания

Понятие о колебательных процессах. Единый подход к колебаниям различной физической природы. Гармонические колебания (механические и электромагнитные) и их характеристики. Дифференциальное уравнение гармонических колебаний. Пружинный, математический и физический маятники. Электрический колебательный контур. Энергия гармонических колебаний. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения. Сложение взаимно перпендикулярных колебаний. Дифференциальное уравнение свободных затухающих колебаний и его решение. Коэффициент затухания, логарифмический декремент, добротность. Апериодический процесс. Вынужденные колебания под действием синусоидальной силы. Дифференциальное уравнение вынужденных колебаний и его решение. Процесс установления колебаний. Амплитуда и фаза вынужденных колебаний. Случай резонанса.

2. Волны

Волновые процессы. Механические волны в упругой среде. Продольные и поперечные волны. Плоские синусоидальные (гармонические) волны. Сферические волны. Уравнение бегущей волны. Длина волны и волновое число. Волновое уравнение. Фазовая скорость. Энергия волны. Принцип суперпозиции волн. Групповая скорость. Вектор Умова. Стоячие волны.

Уравнение плоской электромагнитной волны. Основные свойства электромагнитных волн. Энергия электромагнитных волн. Вектор Пойнтинга.

3. Волновая оптика

Световая волна. Интерференция света. Когерентность и монохроматичность световых волн. Оптическая длина пути. Расчет интерференционной картины от двух когерентных источников. Интерференция в тонких пленках. Дифракция света. Принцип Гюйгенса – Френеля. Метод зон Френеля. Дифракция Френеля на круглом отверстии и диске. Дифракция Фраунгофера на одной щели и на дифракционной решетке. Дифракционная решетка как спектральный прибор. Поляризация света. Естественный и поляризованный свет. Поляризаторы. Закон Малюса. Поляризация света при отражении. Закон Брюстера. Поляризация при двойном лучепреломлении.

4. Квантовая природа излучения

Тепловое излучение. Абсолютно черное тело. Закон Кирхгофа. Закон Стефана – Больцмана. Распределение энергии в спектре абсолютно черного тела. Закон смещения Вина. Квантовая гипотеза и формула Планка. Внешний фотоэффект и его законы. Фотоны. Уравнение Эйнштейна для внешнего фотоэффекта. Масса и импульс фотона. Давление света. Эффект Комптона и его теория.

5. Элементы атомной физики и квантовой механики

Корпускулярно-волновой дуализм свойств вещества. Формула де Бройля. Соотношение неопределенностей как проявление корпускулярно-волнового дуализма свойств материи. Волновая функция и ее статистический смысл. Временное уравнение Шредингера. Стационарные состояния. Уравнение Шредингера для стационарных состояний. Частица в одномерной прямоугольной потенциальной яме. Квантование энергии частицы. Туннельный эффект.

6. Элементы физики атомного ядра и элементарных частиц

Строение атомных ядер. Нуклоны. Массовое и зарядовое числа. Взаимодействие нуклонов и понятие о свойствах и природе ядерных сил. Дефект массы и энергия связи ядра. Радиоактивные превращения атомных ядер. Закономерности и происхождение альфа-, бета- и гамма- излучения атомных ядер. Ядерные реакции и законы сохранения. Реакция деления ядра. Цепная реакция деления. Ядерный реактор. Термоядерные реакции. Элементарные частицы, их классификация и взаимная превращаемость.

ТЕМА № 1

ФИЗИКА КОЛЕБАНИЙ И ВОЛН

Колебаниями называются процессы, характеризующиеся той или иной степенью повторяемости. Таким свойством повторяемости обладают, например, качания маятника, колебания струны, напряжение между обкладками конденсатора в колебательном контуре и т. д.

В зависимости от физической природы повторяющегося процесса различают колебания механические, электромагнитные, электромеханические и т. д.

В зависимости от характера воздействия, оказываемого на колеблющуюся систему, различают свободные (собственные или затухающие), вынужденные, параметрические и автоколебания.

Свободными колебаниями называются колебания, которые происходят в системе, предоставленной самой себе, после выведения ее каким-либо способом из положения равновесия.

Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается внешнему периодически изменяющемуся воздействию.

Автоколебаниями называются такие колебания, при которых моменты времени, когда осуществляются внешние воздействия, задаются самой колеблющейся системой, т. е. система сама управляет внешним воздействием.

Параметрическими называются колебания, при которых за счет внешнего воздействия происходит периодическое изменение какого-либо параметра системы.

Простейшими являются гармонические колебания, то есть такие, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Этот вид колебаний особенно важен, так как, во-первых, колебания в природе и в технике часто имеют характер, очень близкий к гармоническому, и, во-вторых, периодические процессы иной формы могут быть представлены как наложение нескольких гармонических колебаний.

Механические колебания.

1. Собственные колебания.

Собственными называются свободные колебания, возникающие в колебательной системе в отсутствие сил сопротивления (трения).

Колебания в подобной системе описываются уравнением вида

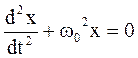, (1)

а сама система называется гармоническим осциллятором.

Примерами гармонических осцилляторов могут служить пружинный, математический и физический маятники (Рис. 1).

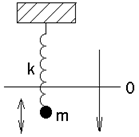
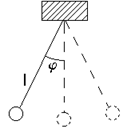
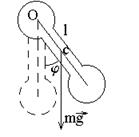
Рис. 1

Пружинный маятник – тело массой m, прикрепленное к пружине с жесткостью k.

Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити длиной l.

Физический маятник – тело, совершающее колебания относительно оси О, находящейся на расстоянии l от его центра инерции С.

Для математического и физического маятников роль величины x в уравнении (1) играет угол отклонения j от положения равновесия. При этом гармоническими являются только малые колебания маятников.

Решение уравнения (1) имеет вид

x = x_m соs (w_ot + a) , (2)

где x_m – амплитуда колебания, наибольшее значение величины, совершающей колебания;

(w₀t + a) – фаза колебания;

a – начальная фаза, т.е. фаза в момент t = 0;

w₀ – собственная круговая частота колебания (число колебаний за 2p секунд).

Используются также следующие понятия:

T – период колебания (время одного полного колебания). T = 2p/w₀.

n – частота колебания (число колебаний за 1 секунду): .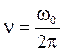

Для рассматриваемых осцилляторов периоды колебаний равны:

пружинного маятника 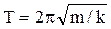; (3)

для математического 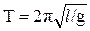; (4)

для физического 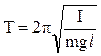. (5)

В формуле (5) величина I – момент инерции физического маятника относительно оси O.

Энергия гармонического осциллятора складывается из кинетической и потенциальной энергий и в любой момент времени остается постоянной:

E = kx_m²/2 или E = mw₀²x_m²/2 . (6)

2. Свободные затухающие колебания

При малых колебаниях и небольших скоростях сила сопротивления среды пропорциональна величине скорости F_сопр = – rV, где r – постоянная, называемая коэффициентом сопротивления. Тогда уравнение колебаний можно представить следующим образом:

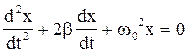, (7)

где ; w₀ – собственная частота колебаний.

Решение уравнения (7) ( при условии w₀>b ) имеет вид

x = x_m0e^-btcos(wt+a), (8)

где 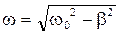. (9)

График этой функции дан на рис. 2.

Рис. 2

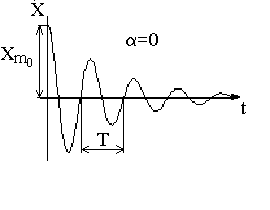Таким образом, данные колебания можно рассматривать как гармонические с частотой w и с амплитудой, убывающей по закону

x_m(t) = x_m0e^-bt (10)

Для характеристики быстроты затухания колебаний применяется несколько величин:

b – коэффициент затухания, величина обратная времени, за которое амплитуда колебаний уменьшится в e раз;

t – время релаксации, за которое амплитуда колебаний уменьшится в e раз: ;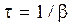

l - логарифмический декремент затухания. По определению – это натуральный логарифм двух последовательных амплитуд колебаний.

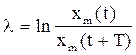. (11)

По физическому смыслу l – это величина, обратная числу колебаний, за время которых амплитуда колебаний уменьшится в e раз. Связь его с коэффициентом затухания выражается формулой

l = bT ; (12)

Q – добротность колебательной системы. По определению Q – это отношение числа p к логарифмическому декременту затухания колебаний:

Q = p/l . (13)

Если в уравнении (7) b³w₀, то колебания в системе невозможны. При выведении ее из положения равновесия происходит апериодический процесс возврата системы в исходное состояние.

3. Вынужденные колебания

Если вынуждающая сила, действующая на колебательную систему, изменяется по гармоническому закону

F = F_m cos(Wt) ,

то дифференциальное уравнение вынужденных колебаний можно представить в виде

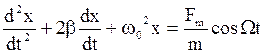, (14)

где b – коэффициент затухания , а w₀ – собственная частота колебаний системы. Это неоднородное дифференциальное уравнение (с правой частью, не равной нулю). Из теории дифференциальных уравнений известно, что общее решение уравнения такого вида представляет собой сумму общего решения однородного уравнения затухающих колебаний, рассмотренного ранее, и частного решения данного неоднородного уравнения. При этом первое убывающее слагаемое играет роль только во время установления колебаний. На рис. 3 показан примерный вид зависимости x(t), описываемой уравнением (14).

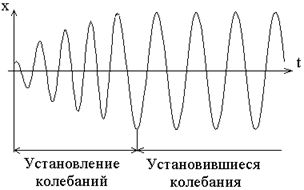B установившемся режиме вынужденные колебания являются гармоническими, незатухающими, происходят с частотой вынуждающей силы W. Их уравнение

x = x_mcos (Wt + j) (15)

Рис. 3

При этом амплитуда x_m вынужденных колебаний равна 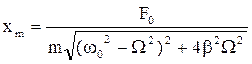, (16) а сдвиг фаз этих колебаний j по отношению к вынуждающей силе определяется из равенства

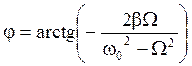. (17)

Зависимость вынужденных колебаний от частоты вынуждающей силы (16) приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Это явление называется резонансом, а соответствующая частота – резонансной частотой. Исследование равенства (16) дает

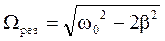. (18)

Рис. 4

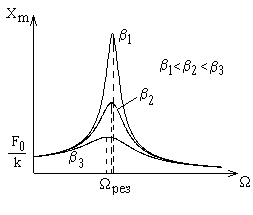Графики зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы W (резонансные кривые), соответствующие различным значениям параметра b, показаны на рис. 4.

4. Сложение гармонических колебаний

При сложении двух гармонических колебаний, одинаково направленных и одинаковой частоты, описываемых уравнениями

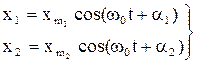, (19)

результирующее колебание будет также гармоническим и иметь частоту w₀:

x = x_mcos(w₀t + a) , (20)

где амплитуда x_m и начальная фаза a равны соответственно:

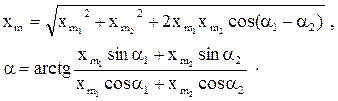(21)

При сложении двух гармонических колебаний одного направления с мало отличающимися частотами, которые задаются уравнениями

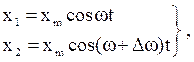(22)

где Dw << w, результирующее колебание является гармоническим с пульсирующей амплитудой. Такие колебания называются биениями.

Уравнение биений имеет вид

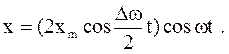(23)

При сложении двух взаимно перпендикулярных колебаний одинаковой частоты, уравнения которых имеют вид

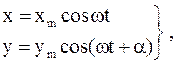(24)

точка движется по траектории

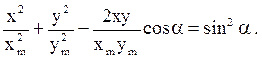(25)

В зависимости от разности фаз a складываемых колебаний возможны частные случаи:

1. a = 0 – точка движется по прямой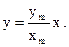

2. a = ±p – точка движется по прямой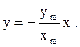

В обоих случаях это гармоническое колебание, происходящее по закону

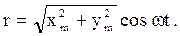(26)

3. a = ±p/2 – точка движется по эллипсу, уравнение которого:

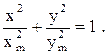(27)