Теорема единственности для двумерного волнового уравнения

Докажем единственность решения волнового уравнения при заданных начальных условиях. Для простоты записи будем считать 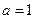, чего можно всегда достигнуть, меняя масштаб времени заменой t на t/a. Для большей наглядности рассмотрим двумерное волновое уравнение, т.е. для u (x,y,t)

(23)

c начальными условиями

(24)

Докажем единственность решения задачи Коши (23) – (24), предполагая, что решение u(x,y,t) имеет непрерывные производные до второго порядка включительно.

Пусть u₁(x,y,t)и u₂(x,y,t) – два решения уравнения (23), удовлетворяющие одним и тем же начальным условиям (24). Тогда разность

будет удовлетворять уравнению (23) и нулевым начальным условиям

(25)

Для доказательства теоремы единственности нам надо теперь показать, что при любых x,y и при всех t >0.

Рассмотрим для этого трехмерное пространство (x,y,t) и возьмем в нем произвольную точку М(x₀,y₀,t₀), причем t₀ >0. Из этой точки как из вершины проведем круговой конус

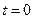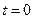до его пересечения с плоскостью (Рис.22). Далее проведем еще одну плоскость , где , и пусть D – область, ограниченная боковой поверхностью конуса S и частями поверхностей и , находящихся внутри конуса. Иначе говоря, D – усеченный круговой конус. Обозначим через σ₀и σ₁ – соответственно нижнее и верхнее основания этого конуса.

Теперь в приведенном ниже выражении произведем указанные в нем операции дифференцирования и приведем подобные члены

В результате получим тождество

Проинтегрируем это тождество по объему, занимаемому областью D. Интеграл от левой части равен нулю, так как u является решением уравнения (23). Интеграл в правой части преобразуем, пользуясь формулой Гаусса-Остроградского, в интеграл по поверхности этой области, составленной из поверхностей S, σ₀и σ₁. В результате получим сумму трех поверхностных интегралов от одного и того же выражения, при записи которого нужно учесть, что производные , стоящие перед скобками, являются производными по направлениям t, x, y и направляющие косинусы будут соответственно равны .

В результате получим

, (26)

где

(27)

На нижнем основании σ₀ усеченного конуса D, в силу начальных условий (25), функция u и все её частные производные первого порядка равны нулю и, следовательно, второй интеграл в (26) равен нулю. На верхнем основании σ₁ имеем

На боковой поверхности конуса S направляющие косинусы нормали удовлетворяют соотношению

(28)

В результате равенство (26) с учетом (27) можно переписать следующим образом

(29)

Первый интеграл с учетом (28) можно преобразовать следующим образом

На боковой поверхности S и, следовательно, этот интеграл неотрицателен, из чего приходится заключить, что второй интеграл в формуле (29) равен нулю, а именно

Отсюда следует, что во всех точках внутри полного конуса с вершиной в точке М(x₀,y₀,t₀) частные производные первого порядка функции u равны нулю и, следовательно сама u равна константе, а поскольку на нижнем основании эта константа в силу (25) равна нулю, то и в точке М(x₀,y₀,t₀) она равна нулю. Поскольку точка М(x₀,y₀,t₀) была нами выбрана произвольно в полупространстве t >0, то составленная нами функция u тождественно равна нулю в этом полупространстве, что и доказывает теорему единственности.